沪科版数学九年级上册二次函数与反比例函数章末十四种重难点题型汇总【提升篇】
试卷更新日期:2023-09-19 类型:同步测试
一、二次函数与一次函数图像综合
-
1. 在同一坐标系中,一次函数y=ax+b与二次函数y=ax2+b的大致图象为( )A、
 B、
B、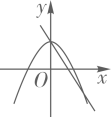 C、
C、 D、
D、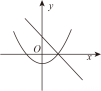 2. 函数和(a是常数,且)在同一平面直角坐标系中的图象可能是( )A、
2. 函数和(a是常数,且)在同一平面直角坐标系中的图象可能是( )A、 B、
B、 C、
C、 D、
D、 3. 已知二次函数和一次函数 , 则这两个函数在同一个平面直角坐标系中的大致图象是( )A、
3. 已知二次函数和一次函数 , 则这两个函数在同一个平面直角坐标系中的大致图象是( )A、 B、
B、 C、
C、 D、
D、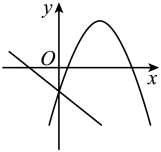 4. 二次函数与一次函数在同一平面直角坐标系中的图象可能是( )A、
4. 二次函数与一次函数在同一平面直角坐标系中的图象可能是( )A、 B、
B、 C、
C、 D、
D、
二、二次函数图像与系数关系
-
5. 如图,抛物线与x轴交于点 , 对称轴为 , 下列结论:①;②;③关于x的方程一定有两个不相等的实数根;④ . 其中结论正确的个数有( )
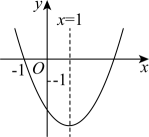 A、1个 B、2个 C、3个 D、4个6. 如图,抛物线与x轴交于点 , 其中 , 下列四个结论:①;②;③;④不等式的解集为 . 其中正确结论的个数是( )
A、1个 B、2个 C、3个 D、4个6. 如图,抛物线与x轴交于点 , 其中 , 下列四个结论:①;②;③;④不等式的解集为 . 其中正确结论的个数是( )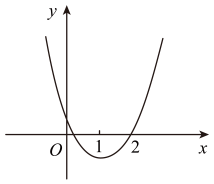 A、1 B、2 C、3 D、47. 如图,二次函数的图象与一次函数的图象交于 , 两点,二次函数的对称轴为 , , 是关于的方程的两个根,有以下结论:①;②;③;④当时,.其中正确的结论是( )
A、1 B、2 C、3 D、47. 如图,二次函数的图象与一次函数的图象交于 , 两点,二次函数的对称轴为 , , 是关于的方程的两个根,有以下结论:①;②;③;④当时,.其中正确的结论是( )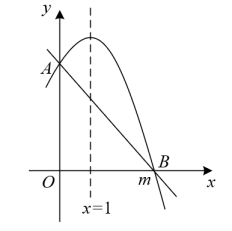 A、①②③④ B、①③④ C、②③④ D、②④8. 二次函数的图象的一部分如图所示,已知图象经过点其对称轴为直线下列结论①;②;③;④;⑤点是抛物线上的两点,则;⑥若抛物线经过点 , 则关于x的一元二次方程的两根分别为 , 正确的有 填序号
A、①②③④ B、①③④ C、②③④ D、②④8. 二次函数的图象的一部分如图所示,已知图象经过点其对称轴为直线下列结论①;②;③;④;⑤点是抛物线上的两点,则;⑥若抛物线经过点 , 则关于x的一元二次方程的两根分别为 , 正确的有 填序号 9. 已知抛物线( , , 是常数且)过和两点,且 , 下列四个结论:;;若抛物线过点 , 则;关于的方程有实数根,则其中正确的结论有( )A、1个 B、2个 C、3个 D、4个
9. 已知抛物线( , , 是常数且)过和两点,且 , 下列四个结论:;;若抛物线过点 , 则;关于的方程有实数根,则其中正确的结论有( )A、1个 B、2个 C、3个 D、4个三、根据二次函数性质求特定值
-
10. 把二次函数的图象作关于y轴的对称变换,所得图象的解析式为 , 若成立,则m的最小整数值为( )A、2 B、3 C、4 D、511. 已知二次函数 , 将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新的函数图象(如图所示),当直线与新图像有3个交点时,m的值是( )
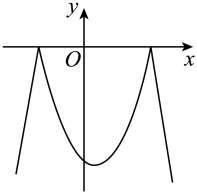 A、 B、-2 C、-2或3 D、-6或-212. 如图, 将抛物线沿轴翻折, 翻折前后的两条抛物线构成一个新图象.若直线与这个新图象有3个公共点, 则的值为( )
A、 B、-2 C、-2或3 D、-6或-212. 如图, 将抛物线沿轴翻折, 翻折前后的两条抛物线构成一个新图象.若直线与这个新图象有3个公共点, 则的值为( ) A、或2 B、或2 C、2或4 D、或4
A、或2 B、或2 C、2或4 D、或4四、根据二次函数的性质求字母取值范围
-
13. 已知点在直线上,点在抛物线上,若且 , 则的取值范围是( )A、 B、 C、 D、14. 已知二次函数及一次函数 , 将二次函数在轴下方的图像沿轴翻折到轴上方,图象的其余部分不变,得到一个新图象(如图所示),当直线与新图象有4个交点时,的取值范围是( )
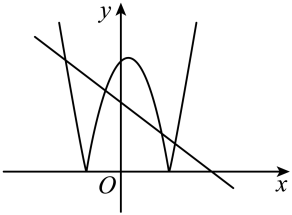 A、 B、 C、 D、
A、 B、 C、 D、五、二次函数平移问题
-
15. 将抛物线先向右平移个单位,再向上平移个单位,所得抛物线对应的函数表达式为( )A、 B、 C、 D、16. 抛物线可以由抛物线平移得到,则下列平移过程正确的是( )A、先向左平移个单位,再向上平移个单位 B、先向左平移个单位,再向下平移个单位 C、先向右平移个单位,再向下平移个单位 D、先向右平移个单位,再向上平移个单位17. 如图,水池中心点O处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点O在同一水平面.安装师傅调试发现,喷头高时,水柱落点距O点;喷头高时,水柱落点距O点 . 那么喷头高m时,水柱落点距O点 .
 18. 如图,抛物线L:与x轴交于 , B两点,与y轴交于点 , D为抛物线L的顶点.
18. 如图,抛物线L:与x轴交于 , B两点,与y轴交于点 , D为抛物线L的顶点. (1)、求抛物线L的表达式.(2)、将抛物线L向右平移,平移后所得的抛物线与x轴交于点 , , 交y轴于点 , 顶点为 . 若 , 求抛物线的表达式.19. 如图,已知二次函数的图象经过点 , 点。
(1)、求抛物线L的表达式.(2)、将抛物线L向右平移,平移后所得的抛物线与x轴交于点 , , 交y轴于点 , 顶点为 . 若 , 求抛物线的表达式.19. 如图,已知二次函数的图象经过点 , 点。 (1)、求二次函数的表达式和顶点坐标。(2)、点在该二次函数图象上,当时,求n的值。(3)、已知 , , 若将该二次函数的图象向上平移k(k>0)个单位后与线段AB有交点,请结合图象,直接写出k的取值范围。20. 如图,抛物线与x轴的一个交点为 , 与y轴交于点B.
(1)、求二次函数的表达式和顶点坐标。(2)、点在该二次函数图象上,当时,求n的值。(3)、已知 , , 若将该二次函数的图象向上平移k(k>0)个单位后与线段AB有交点,请结合图象,直接写出k的取值范围。20. 如图,抛物线与x轴的一个交点为 , 与y轴交于点B.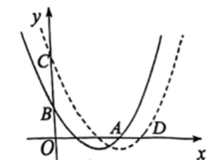 (1)、求h的值及点B的坐标.(2)、将该抛物线向右平移个单位长度后,与y轴交于点C,且点A的对应点为D,若 , 求m的值.
(1)、求h的值及点B的坐标.(2)、将该抛物线向右平移个单位长度后,与y轴交于点C,且点A的对应点为D,若 , 求m的值.六、利用二次函数图像解一元二次方程
-
21. 若二次函数的图象经过点 , , 则关于x的方程的解为( )A、 , B、 , C、 , D、 ,22. 二次函数的部分对应值列表如下:
x
…
-3
0
1
3
5
…
y
…
7
-8
-9
-5
7
…
则一元二次方程的解为 .
23. 已知二次函数的图像与x轴交于点 , 则关于x的一元二次方程的解为.七、估算一元二次方程近似根
-
24. 如表是二次函数的自变量x与函数值y的部分对应值,那么方程的一个根的取值范围是( )
x
…
1
1.1
1.2
1.3
1.4
…
y
…
-1
-0.49
0.04
0.59
1.16
…
A、 B、 C、 D、25. 由下表估算一元二次方程x2+12x=15的一个根的范围,正确的是( )x
1.0
1.1
1.2
1.3
x2+12x
13
14.41
15.84
17.29
A、1.0<x<1.1 B、1.1<x<1.2 C、1.2<x<1.3 D、14.41<x<15.8426. 根据下列表格对应值,判断关于的方程的一个解的范围是( )1.1
1.2
1.3
1.4
-0.59
0.84
2.29
3.76
A、1.1<x<1.2 B、1.2<x<1.3 C、1.3<x<1.4 D、无法判定27. 在求解方程时,先在平面直角坐标系中画出函数的图象,观察图象与x轴的两个交点,这两个交点的横坐标可以看作是方程的近似解,分析右图中的信息,方程的近似解是( ) A、 , B、 , C、 , D、 ,28. 根据下面表格中的对应值:
A、 , B、 , C、 , D、 ,28. 根据下面表格中的对应值:x
3.23
3.24
3.25
3.26
ax2+bx+c
﹣0.06
﹣0.02
0.03
0.09
判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
A、3.22<x<3.23 B、3.23<x<3.24 C、3.24<x<3.25 D、3.25<x<3.26八、二次函数与一元二次不等式
-
29. 如图,直线与抛物线交于两点,则关于x的不等式的解集是.
 30. 如图,抛物线y=ax2+c与直线y=kx+b交于A(-1,m),B(2,n)两点,则不等式ax2-kx+c<b的解集是.
30. 如图,抛物线y=ax2+c与直线y=kx+b交于A(-1,m),B(2,n)两点,则不等式ax2-kx+c<b的解集是.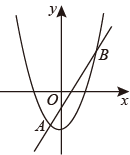 31. 已知二次函数与一次函数交于、两点 , 当时,至少存在一个x使得成立,则m的取值范围是( )A、 B、 C、 D、32. 如图,抛物线( , , 为常数,且)交轴于 , 两点,则不等式的解为.
31. 已知二次函数与一次函数交于、两点 , 当时,至少存在一个x使得成立,则m的取值范围是( )A、 B、 C、 D、32. 如图,抛物线( , , 为常数,且)交轴于 , 两点,则不等式的解为.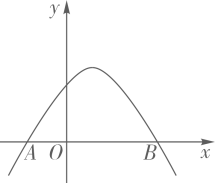
九、二次函数的实际应用
-
33. 据省统计局公布的数据,合肥市2021年第一季度GDP总值约为2.4千亿元人民币,若我市第三季度GDP总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )A、 B、 C、 D、34. 加强劳动教育,落实五育并举.孝礼中学在当地政府的支持下,建成了一处劳动实践基地.2023年计划将其中的土地全部种植甲乙两种蔬菜.经调查发现:甲种蔬菜种植成本y(单位;元/)与其种植面积x(单位:)的函数关系如图所示,其中;乙种蔬菜的种植成本为50元/ .
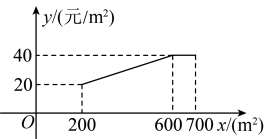 (1)、当时,元/;(2)、设2023年甲乙两种蔬菜总种植成本为W元,如何分配两种蔬菜的种植面积,使W最小?(3)、学校计划今后每年在这土地上,均按(2)中方案种植蔬菜,因技术改进,预计种植成本逐年下降,若甲种蔬菜种植成本平均每年下降 , 乙种蔬菜种植成本平均每年下降 , 当a为何值时,2025年的总种植成本为元?35. 为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)、当时,元/;(2)、设2023年甲乙两种蔬菜总种植成本为W元,如何分配两种蔬菜的种植面积,使W最小?(3)、学校计划今后每年在这土地上,均按(2)中方案种植蔬菜,因技术改进,预计种植成本逐年下降,若甲种蔬菜种植成本平均每年下降 , 乙种蔬菜种植成本平均每年下降 , 当a为何值时,2025年的总种植成本为元?35. 为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
 (1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、若矩形空地的面积为160m2 , 求x的值;(3)、若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
(1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、若矩形空地的面积为160m2 , 求x的值;(3)、若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.甲
乙
丙
单价(元/棵)
14
16
28
合理用地(m2/棵)
0.4
1
0.4
36. 如图1,有一座抛物线形拱桥,某正常水位时,桥下的水面宽20米,拱顶到水面的距离为6米,到桥面的距离为4米,相邻两支柱间的距离均为5米,建立直角坐标系如图2. (1)、求抛物线的函数表达式.(2)、求支柱的长度.(3)、随着水位的上升,桥下水面的宽度逐渐减小.一艘货船在水面上的部分的横截面是边长为5米的正方形,当水位上升0.75米时,这艘货船能否顺利通过拱桥?请说说你的理由.37. 卡塔尔世界杯完美落幕.在一场比赛中,球员甲在离对方球门30米处的点起脚吊射(把球高高地挑过守门员的头顶,射入球门),假如球飞行的路线是一条抛物线,在离球门14米时,足球达到最大高度8米.如图所示,以球员甲所在位置点为原点,球员甲与对方球门所在直线为轴,建立平面直角坐标系.
(1)、求抛物线的函数表达式.(2)、求支柱的长度.(3)、随着水位的上升,桥下水面的宽度逐渐减小.一艘货船在水面上的部分的横截面是边长为5米的正方形,当水位上升0.75米时,这艘货船能否顺利通过拱桥?请说说你的理由.37. 卡塔尔世界杯完美落幕.在一场比赛中,球员甲在离对方球门30米处的点起脚吊射(把球高高地挑过守门员的头顶,射入球门),假如球飞行的路线是一条抛物线,在离球门14米时,足球达到最大高度8米.如图所示,以球员甲所在位置点为原点,球员甲与对方球门所在直线为轴,建立平面直角坐标系. (1)、求满足条件的抛物线的函数表达式;(2)、如果葡萄牙球员罗站在球员甲前3米处,罗跳起后最高能达到2.88米,那么罗能否在空中截住这次吊射?38. 如图,灌溉车为绿化带浇水,喷水口H离地竖直高度为1.2m.可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形 , 其水平宽度 , 竖直高度.下边缘抛物线是由上边缘抛物线向左平移得到,上边抛物线最高点A离喷水口的水平距离为2m,高出喷水口0.4m,灌溉车到绿化带的距离为d(单位:m).
(1)、求满足条件的抛物线的函数表达式;(2)、如果葡萄牙球员罗站在球员甲前3米处,罗跳起后最高能达到2.88米,那么罗能否在空中截住这次吊射?38. 如图,灌溉车为绿化带浇水,喷水口H离地竖直高度为1.2m.可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形 , 其水平宽度 , 竖直高度.下边缘抛物线是由上边缘抛物线向左平移得到,上边抛物线最高点A离喷水口的水平距离为2m,高出喷水口0.4m,灌溉车到绿化带的距离为d(单位:m). (1)、求上边缘抛物线的函数解析式,并求喷出水的最大射程;(2)、求下边缘抛物线与x轴的正半轴交点B的坐标;(3)、要使灌溉车行驶时喷出的水能浇灌到整个绿化带,直接写出d的取值范围.39. 如图,抛物线与轴交于 , 两点,与轴交于点 . 已知点的坐标是 , 抛物线的对称轴是直线 .
(1)、求上边缘抛物线的函数解析式,并求喷出水的最大射程;(2)、求下边缘抛物线与x轴的正半轴交点B的坐标;(3)、要使灌溉车行驶时喷出的水能浇灌到整个绿化带,直接写出d的取值范围.39. 如图,抛物线与轴交于 , 两点,与轴交于点 . 已知点的坐标是 , 抛物线的对称轴是直线 . (1)、直接写出点的坐标;(2)、在对称轴上找一点 , 使的值最小.求点的坐标和的最小值;(3)、第一象限内的抛物线上有一动点 , 过点作轴,垂足为 , 连接交于点 . 依题意补全图形,当的值最大时,求点的坐标.40. 已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(-2,0),点P是线段AB上方抛物线上的一个动点.
(1)、直接写出点的坐标;(2)、在对称轴上找一点 , 使的值最小.求点的坐标和的最小值;(3)、第一象限内的抛物线上有一动点 , 过点作轴,垂足为 , 连接交于点 . 依题意补全图形,当的值最大时,求点的坐标.40. 已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(-2,0),点P是线段AB上方抛物线上的一个动点. (1)、求抛物线的解析式;(2)、当点P运动到什么位置时,△PAB的面积有最大值?(3)、过点P作x轴的垂线,交线段AB于点D,再过点P作PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.
(1)、求抛物线的解析式;(2)、当点P运动到什么位置时,△PAB的面积有最大值?(3)、过点P作x轴的垂线,交线段AB于点D,再过点P作PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.十、反比例函数k的几何特性
-
41. 如图,点A是反比例函数的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )
 A、3 B、-6 C、6 D、-342. 如图,在平面直角坐标系中,线段的端点点A、点D分别在y轴与x轴上.且与反比例函数交于点B、点C,且 , 面积为3,则k的值为( )
A、3 B、-6 C、6 D、-342. 如图,在平面直角坐标系中,线段的端点点A、点D分别在y轴与x轴上.且与反比例函数交于点B、点C,且 , 面积为3,则k的值为( ) A、 B、 C、 D、43. 两个反比例函数:和:在第一象限内的图象如图所示,设点P在上,轴于点C,交于点A,轴于点D,交于点B,则四边形的面积为( )
A、 B、 C、 D、43. 两个反比例函数:和:在第一象限内的图象如图所示,设点P在上,轴于点C,交于点A,轴于点D,交于点B,则四边形的面积为( ) A、1 B、2 C、3 D、444. 如图,矩形的顶点A,C分别在y轴、x轴的正半轴上,点D在上,且 , 反比例函数的图象经过点D及矩形的对称中心M,连接 . 若的面积为3,则k的值为( )
A、1 B、2 C、3 D、444. 如图,矩形的顶点A,C分别在y轴、x轴的正半轴上,点D在上,且 , 反比例函数的图象经过点D及矩形的对称中心M,连接 . 若的面积为3,则k的值为( )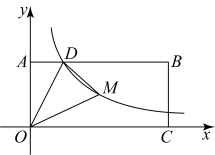 A、2 B、3 C、4 D、545. 如图,过y轴正半轴上一点P作x轴的平行线,分别与反比例函数和图像相交于点A和点B,C是x轴上一点.若的面积为4,则k的值为 .
A、2 B、3 C、4 D、545. 如图,过y轴正半轴上一点P作x轴的平行线,分别与反比例函数和图像相交于点A和点B,C是x轴上一点.若的面积为4,则k的值为 . 46. 如图,直线与双曲线相交于点 , 轴于点 , 以为边在右侧作正方形 , 与双曲线相交于点 , 连结、 .
46. 如图,直线与双曲线相交于点 , 轴于点 , 以为边在右侧作正方形 , 与双曲线相交于点 , 连结、 .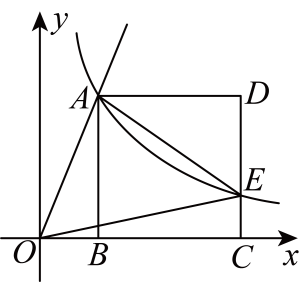 (1)、当时,求点的坐标;(2)、当时,求的值;(3)、是否存在实数 , 满足 , 若存在,求出的值;若不存在,请说明理由.
(1)、当时,求点的坐标;(2)、当时,求的值;(3)、是否存在实数 , 满足 , 若存在,求出的值;若不存在,请说明理由.十一、反比例函数图像上点的坐标意义
-
47. 如图,直线、与双曲线分别相交于点 . 若四边形的面积为4,则的值是( )
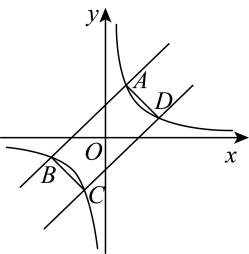 A、 B、 C、 D、148. 如图,菱形在第二象限内, , 反比例函数的图象经过点 , 交边于点 , 若的面积为 , 则的值为( )
A、 B、 C、 D、148. 如图,菱形在第二象限内, , 反比例函数的图象经过点 , 交边于点 , 若的面积为 , 则的值为( ) A、 B、 C、 D、49. 如图,点在轴的正半轴上,点在第一象限, , 反比例函数的图像经过点 , 反比例函数的图像经过点 . 若 , 则的值为( )
A、 B、 C、 D、49. 如图,点在轴的正半轴上,点在第一象限, , 反比例函数的图像经过点 , 反比例函数的图像经过点 . 若 , 则的值为( ) A、2 B、3 C、4 D、550. 如图,在平面直角坐标系中,的边在x轴正半轴上,其中 , , 点C为斜边的中点,反比例函数的图象过点C且交线段于点D,连接 , , 若 , 则的值为( )
A、2 B、3 C、4 D、550. 如图,在平面直角坐标系中,的边在x轴正半轴上,其中 , , 点C为斜边的中点,反比例函数的图象过点C且交线段于点D,连接 , , 若 , 则的值为( ) A、 B、 C、 D、351. 如图,在平面直角坐标系中,的边在y轴上,点C在第一象限内,点B为的中点,反比例函数的图象经过B , C两点.若的面积是6,则k的值为 .
A、 B、 C、 D、351. 如图,在平面直角坐标系中,的边在y轴上,点C在第一象限内,点B为的中点,反比例函数的图象经过B , C两点.若的面积是6,则k的值为 . 52. 如图,一次函数与反比例函数的图象交于、两点,与轴交于点.
52. 如图,一次函数与反比例函数的图象交于、两点,与轴交于点.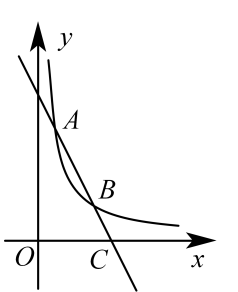 (1)、求一次函数与反比例函数的解析式;(2)、若点在轴上,且的面积为 , 求点的坐标.
(1)、求一次函数与反比例函数的解析式;(2)、若点在轴上,且的面积为 , 求点的坐标.十二、反比例函数图像性质应用
-
53. 已知反比例函数 , 下列结论中不正确的是( )A、其图像分别位于第二、四象限 B、其图像关于原点对称 C、其图像经过点(2,-4) D、若点A(x1 , y1),B(x2 , y2)都在图像上,且x1<x2 , 则y1<y254. 若点、、在反比例函数的图象上,则、、的大小关系是( )A、 B、 C、 D、55. 探究函数的图像发现,可以由的图像先向右平移2个单位,再向上平移3个单位得到.根据以上信息判断,下列直线中与函数的图像没有公共点的是( )A、经过点且平行于x轴的直线 B、经过点且平行于x轴的直线 C、经过点且平行于y轴的直线 D、经过点且平行于y轴的直线56. 如图,取一根长的匀质木杆,用细绳绑在木杆的中点O并将其吊起来,在中点O的左侧距离中点处挂一个重的物体,在中点O的右侧用一个弹簧秤向下拉,使木杆处于水平状态.弹簧秤与中点O的距离L(单位:)及弹簧秤的示数F(单位:N)满足 . 以L的数值为横坐标,F的数值为纵坐标建立直角坐标系.则F关于L的函数图象大致是( )
 A、
A、 B、
B、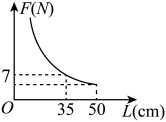 C、
C、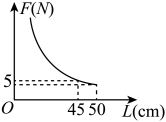 D、
D、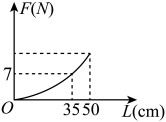 57. 如图,是坐标原点,点在轴上,点在反比例函数图象上,在等腰三角 , , 且三角形的面积为 , 则的值( )
57. 如图,是坐标原点,点在轴上,点在反比例函数图象上,在等腰三角 , , 且三角形的面积为 , 则的值( ) A、 B、 C、 D、
A、 B、 C、 D、十三、反比例函数共存问题
-
58. 函数与在同一平面直角坐标系中的图象可能是( )A、
 B、
B、 C、
C、 D、
D、 59. 已知反比例函数在第一象限内的图象与一次函数的图象如图所示,则函数的图象可能为( )
59. 已知反比例函数在第一象限内的图象与一次函数的图象如图所示,则函数的图象可能为( ) A、
A、 B、
B、 C、
C、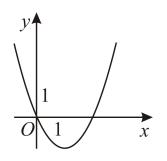 D、
D、 60. 如图是反比例函数的图像,则一次函数的图像大致是( )
60. 如图是反比例函数的图像,则一次函数的图像大致是( ) A、
A、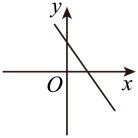 B、
B、 C、
C、 D、
D、 61. 一次函数和反比例函数在同一个平面直角坐标系中的图象如图所示,则二次函数的图象可能是( )
61. 一次函数和反比例函数在同一个平面直角坐标系中的图象如图所示,则二次函数的图象可能是( ) A、
A、 B、
B、 C、
C、 D、
D、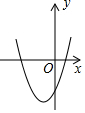
十四、反比例函数实际应用
-
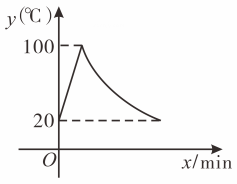
62. 某学校的自动饮水机,开机加热时水温每分钟上升 , 水温到时停止加热.此后水温开始下降.水温与开机通电时间成反比例关系.若水温在时接通电源.一段时间内,水温y与通电时间x之间的函数关系如图所示.
 (1)、水温从加热到 , 需要;(2)、求水温下降过程中,y与x的函数关系式,并写出自变量取值范围;(3)、如果上午8点接通电源,那么8:20之前,不低于的时间有多少?63. 五一假期,小王一家从杭州到温州自驾游,已知杭州到温州市区A处的路程为300千米,小王家的车油箱的容积为55升,小王把油箱加满后驾驶汽车从杭州出发.(1)、求汽车行驶的总路程s(单位:千米)与平均耗油量b(单位:升/千米)的函数表达式.(2)、小王以平均每千米耗油0.1升的速度驾驶汽车到达温州市区A处,休整后沿图示路线继续出发,先到雁荡山B处,再到楠溪江C处,最后到洞头D处.由于下雨,从A处开始直到D处小王降低了车速,此时平均每千米的耗油量增加了20%.如果小王始终以此速度行驶,不需加油能否到达洞头D处?如果不能,至少还需加多少油?
(1)、水温从加热到 , 需要;(2)、求水温下降过程中,y与x的函数关系式,并写出自变量取值范围;(3)、如果上午8点接通电源,那么8:20之前,不低于的时间有多少?63. 五一假期,小王一家从杭州到温州自驾游,已知杭州到温州市区A处的路程为300千米,小王家的车油箱的容积为55升,小王把油箱加满后驾驶汽车从杭州出发.(1)、求汽车行驶的总路程s(单位:千米)与平均耗油量b(单位:升/千米)的函数表达式.(2)、小王以平均每千米耗油0.1升的速度驾驶汽车到达温州市区A处,休整后沿图示路线继续出发,先到雁荡山B处,再到楠溪江C处,最后到洞头D处.由于下雨,从A处开始直到D处小王降低了车速,此时平均每千米的耗油量增加了20%.如果小王始终以此速度行驶,不需加油能否到达洞头D处?如果不能,至少还需加多少油? 64. 在实验课上,小明做了一个试验.如图,在仪器左边托盘(固定)中放置一个物体,在右边托盘(可左右移动)中放置一个可以装水的容器,容器的质量为 . 在容器中加入一定质量的水,可以使仪器左右平衡.改变托盘与点的距离()(),记录容器中加入的水的质量,得到下表:
64. 在实验课上,小明做了一个试验.如图,在仪器左边托盘(固定)中放置一个物体,在右边托盘(可左右移动)中放置一个可以装水的容器,容器的质量为 . 在容器中加入一定质量的水,可以使仪器左右平衡.改变托盘与点的距离()(),记录容器中加入的水的质量,得到下表:
托盘与点的距离
30
25
20
15
10
容器与水的总质量
10
12
15
20
30
加入的水的质量
5
7
10
15
25
把上表中的与各组对应值作为点的坐标,在平面直角坐标系中描出这些点,并用光滑的曲线连接起来,得到如图所示的关于的函数图象.
 (1)、请在该平面直角坐标系中作出关于的函数图象;(2)、观察函数图象,并结合表中的数据:
(1)、请在该平面直角坐标系中作出关于的函数图象;(2)、观察函数图象,并结合表中的数据:①猜测与之间的函数关系,并求关于的函数表达式;
②求关于的函数表达式;
③当时,随的增大而(填“增大”或“减小”),随的增大而(填“增大”或“减小”),的图象可以由的图象向(以“上”或“下”或“左”或“右”)平移得到.
(3)、若在容器中加入的水的质量(g)满足 , 求托盘与点的距离(cm)的取值范围.