四川省绵阳市游仙区2023-2024学年九年级上学期数学开学考试试卷

试卷更新日期：2023-09-19 类型：开学考试

进入出卷网下载

一、选择题(每小题3分,共36分)

1. 下列各式计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $4 \sqrt{3} - 3 \sqrt{3} = 1$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $\sqrt{12} \div 2 = \sqrt{6}$

查看试题解析
2. 《义务教育课程标准（2022年版）》首次把学生学会炒菜纳入劳动教育课程，并做出明确规定.某班有7名学生已经学会炒的菜品的种数依次为：3，5，4，6，3，3，4，则这组数据的众数和中位数分别是（）

A、3，4 B、4，3 C、3，3 D、4，4

查看试题解析
3. 由下列长度组成的各组线段中，不能组成直角三角形的是（）

A、 $\sqrt{2} c m ， \sqrt{2} c m ， 2 c m$ B、 $1 c m ， 2 c m ， \sqrt{3} c m$ C、 $\sqrt{3} c m ， 2 c m ， \sqrt{5} c m$ D、 $\sqrt{2} c m ， \sqrt{3} c m ， 1 c m$

查看试题解析
4. 如图，在▱ABCD中，BE平分∠ABC交DC于点E.若∠A=60° ，则∠DEB的大小为 (　　)

A、130°　　　　 B、125°　　　　 C、120°　　　　 D、115°

查看试题解析
5. 若一次函数 $y = k x + b$ 的图象如图所示，则下列说法正确的是（）

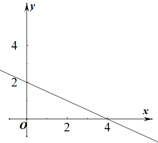A、 $k > 0$ B、 $b = 2$ C、y随x的增大而增大 D、 $x = 3$ 时， $y = 0$

查看试题解析
6. 在2022年中考体育测试中，某班15名女生选择立定跳远项目，她们的成绩情况统计如表：
成绩(米)
1.50
1.60
1.65
1.70
1.75
人数
2
3
2
5
3
则这15名女生立定跳远成绩的众数和中位数分别是 (　　)

A、1.70，1.70　　　　 B、1.70，1.65　　　　 C、1.65，1.65　　　　 D、1.65，1.70

查看试题解析
7. 如图所示，D、E、F分别是△ABC三边的中点，连接EF、DE、BE ，下列条件中不能使四边形BDEF成为菱形的是 (　　)

A、AB=BC　　　　 B、BE平分∠ABC　　　　 C、EF=EC　　　　 D、BE⊥AC

查看试题解析
8. 如图，在平面直角坐标系中，已知点 $O (0 ， 0)$ ， $A (2 ， 4)$ ，以点 $O$ 为圆心， $O A$ 长为半径画弧，交 $x$ 轴的正半轴于 $B$ 点，则点 $B$ 的坐标是（）

A、 $(2 \sqrt{5} ， 0)$ B、 $(2 \sqrt{3} ， 0)$ C、 $(0 ， 2 \sqrt{5})$ D、 $(0 ， 2 \sqrt{3})$

查看试题解析
9. 如图，一直线与两坐标轴的正半轴分别交于A ， B两点，P是线段AB上任意一点(不包括端点)，过点P分别作两坐标轴的垂线，与两坐标轴围成的长方形的周长为8，则该直线的函数表达式是 (　　)

A、y=x+4　　　　 B、y=x+8　　　　 C、y=-x+4　　　　 D、y=-x+8

查看试题解析
10. 如图所示的是一个三级台阶，它的每一级的长、宽和高分别是50 cm、30 cm、10 cm，A和B是这个台阶的两个相对的顶点，A点有一只壁虎，它想到B点去吃可口的食物，请你想一想，这只壁虎从A点出发，沿着台阶面爬到B点，至少需爬(　　)

A、13 cm　　　　 B、40 cm　　　　 C、130 cm　　　　 D、169 cm

查看试题解析
11. 如图，将▱ABCD沿对角线BD折叠，使点A落在点E处，DE交BC于点F ，若∠ABD=48° ， ∠CFD=40° ，则∠E的度数为 (　　)

A、102°　　 B、112°　　 C、122°　　 D、92°

查看试题解析

12. 某科技小组在网上获取了声音在空气中传播的速度与空气中的温度之间的关系的一些数据(如表).下列说法：①在这个变化过程中，自变量是温度，因变量是声速；②空气中的温度越高，声音传播的速度越快；③声速y(m/s)与温度x(℃)之间的关系式可以是y=0.6x+330；④温度每升高10 ℃，声速增加6 m/s.其中正确的有（）

温度x(℃)	声速y(m/s)
-20	318
-10	324
0	330
10	336
20	342
30	348

A、1个　　　　 B、2个　　　　 C、3个　　　　 D、4个

查看试题解析

二、填空题(每小题3分,共18分

13. 若式子 $\sqrt{x - 19}$ 在实数范围内有意义，则实数x的取值范围是.

查看试题解析
14. 如图，直线y=2x与y=kx+b相交于点P(m ， 2)，则关于x的方程kx+b=2的解是.

查看试题解析
15. 已知一个菱形的周长为52 cm，一条对角线长为10 cm，则另一条对角线长为cm.

查看试题解析
16. 如图，一次函数y= $\frac{4}{3}$ x-4的图象与x轴，y轴分别交于点A ，点B ，过点A作直线l将△ABO分成周长相等的两部分，则直线l的函数解析式为.

查看试题解析
17. 新定义：[a ， b]为一次函数y=ax+b(a≠0，a ， b为实数)的“关联数”.若“关联数”为[3，m-2]的一次函数是正比例函数，则点(1-m ， 1+m)在第象限内.

查看试题解析
18. 四边形ABCD是平行四边形，AB=6，∠BAD的平分线交直线BC于点E ，若CE=2，则▱ABCD的周长为.

查看试题解析

三、解答题(共46分

19. 计算：

(1)、2 $\sqrt{12} + 3 \sqrt{1 \frac{1}{3}} - \sqrt{2} \times \sqrt{6}$ ；　

(2)、 $\sqrt{48} \div \sqrt{3} + | 1 - \sqrt{3} | - \frac{\sqrt{8} - \sqrt{6}}{\sqrt{2}}$ .

查看试题解析
20. 化简求值：

(1)、已知a= $\sqrt{5}$ -2，求代数式a³+4a²-a+6的值；

(2)、已知x= $\sqrt{3}$ -2，y= $\sqrt{3}$ +2，求 $\frac{y}{x} + \frac{x}{y}$ 的值.

查看试题解析
21. 如图，在Rt△ABC中，∠ACB=90° ，点D为BC上的一点，将△ACD沿AD折叠，点C恰好落在边AB上的点E处，且BD=4，CD= $\sqrt{7}$ .

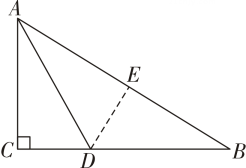(1)、求BE的长；

(2)、求AC的长.

查看试题解析
22. 如图，在平面直角坐标系中，边长为2的正方形ABCD在第一象限内，AD∥y轴，点A的坐标为(5，3)，已知直线l：y= $\frac{1}{2}$ x-2.

(1)、将直线l向上平移m个单位，使平移后的直线恰好经过点A ，求m的值；

(2)、在(1)的条件下，平移后的直线与正方形的边长BC交于点E ，求△ABE的面积.

查看试题解析
23. 2021年12月9日，“天宫课堂”第一课正式开讲，神舟十三号乘组航天员翟志刚、王亚平、叶光富在中国空间站进行太空授课，神奇的太空实验堪称宇宙级精彩!某校组织全校学生进行了“航天知识竞赛”，现从八年级A班和B班中各抽取20名学生的竞赛成绩(单位：分，百分制)进行调查分析，成绩如表：
A班
90
89
100
96
97
98
89
97
87
100
98
95
99
98
77
87
93
92
84
94
B班
78
86
92
95
97
86
76
91
90
99
100
97
89
97
85
91
100
95
100
96
【整理数据】

　频数
班级　

76≤x
≤80
81≤x
≤85
86≤x
≤90
91≤x
≤95
96≤x
≤100
A班
1
1
5
4
9
B班
2
1
4
5
8
【分析数据】根据以上数据进行统计分析：

　统计量
班级　　

平均数
中位数
众数
方差
A班
93
94.5
b
35.3
B班
92
a
97，100
46.9
根据以上信息，解答下列问题：

(1)、表格中的a= ， b=；

(2)、请你根据以上统计信息，分析哪个班在本次活动中整体水平较高且稳定；

(3)、若全校八年级共有学生800人，请你估计本次知识竞赛中分数在90分以上的人数.

查看试题解析
24. 如图，在平面直角坐标系xOy中，直线y=- $\frac{4}{3}$ x+4与x轴、y轴分别交于点A、点B ，点D在y轴的负半轴上，将△DAB沿直线AD折叠，点B恰好落在x轴正半轴上的点C处.

(1)、求AB的长.

(2)、求点C和点D的坐标.

(3)、y轴上是否存在一点P ，使得S_△_PAB= $\frac{1}{2}$ S_△_OCD?若存在，直接写出点P的坐标；若不存在，请说明理由.

查看试题解析

A班	90	89	100	96	97	98	89	97	87	100
A班	98	95	99	98	77	87	93	92	84	94
B班	78	86	92	95	97	86	76	91	90	99
B班	100	97	89	97	85	91	100	95	100	96

成绩(米)	1.50	1.60	1.65	1.70	1.75
人数	2	3	2	5	3