苏科版数学七年级上册有理数章末九大典型题型汇总(基础巩固篇)
试卷更新日期:2023-09-19 类型:同步测试
一、正、负数的意义
-
1. 我国古代《九章算术》中注有“今两算得失相反,要令正负以名之”.是今有两数若其意义相反,则分别叫做正数与负数,如果向北走步记作步,那么向南走步记作( )A、步 B、步 C、 D、步2. 在生产图纸上通常用来表示轴的加工要求,这里表示直径是 , 和是指直径在到之间的产品都属于合格产品.现加工一批轴,尺寸要求是 , 则下面产品合格的是( )A、 B、 C、 D、3. 某单位开展了职工健步走活动,职工每天健步走5000步即为达标.若小夏走了6200步,记为+1200步,小辰走了4800步,记为步.4. 中国人很早就开始使用负数,中国古代数学著作《九章算术》的方程一章,在世界数学史上首次引入负数.下图是小明家长11月份的微信账单,如果收入3377.51元记作元,那么支出5333.73元记作元.
 5. 下列各数中,负数有 ( )A、2个 B、3个 C、4个 D、5个
5. 下列各数中,负数有 ( )A、2个 B、3个 C、4个 D、5个二、有理数的概念及分类
-
6. 把下列各数填在相应的大括号内:﹣5,|﹣ |,﹣12,0,﹣3.14,+1.99,﹣(﹣6), ,200%,15%.(1)、正数集合:{ …};(2)、负数集合:{ …};(3)、整数集合:{ …};(4)、分数集合:{ …}.7. 下面的大括号表示一些数的集合,把下列各数填入相应的大括号里
正有理数集:{ ……}
整数集:{ ……}
负分数集:{ ……}
自然数集:{ ……}
8. 下面说法:①-a 一定是负数;②若|a|=|b|,则 a=b;③一个有理数中不是整数就是分数;④一个有理数不是正数就是负数.⑤绝对值等于它本身的数是正数;其中正确的个数有( )A、1 个 B、2 个 C、3 个 D、4 个9. 下列说法不正确的是( )A、有理数可分为正整数、正分数、0、负整数、负分数 B、一个有理数不是分数就是整数 C、一个有理数不是正数就是负数 D、若一个数是整数,则这个数一定是有理数三、利用数轴表示大小
-
10. 有理数 , 在数轴上的对应点的位置如图所示,则正确的结论是( )
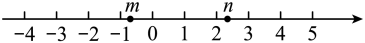 A、 B、 C、 D、11. 若为有理数, , , 且 , 那么的大小关系是( )A、 B、 C、 D、12. 设 , , 且 , 用“”号把、、、连接起来为 .13. 实数a在数轴上的位置如图所示,则 ,1,0的大小顺序是( )
A、 B、 C、 D、11. 若为有理数, , , 且 , 那么的大小关系是( )A、 B、 C、 D、12. 设 , , 且 , 用“”号把、、、连接起来为 .13. 实数a在数轴上的位置如图所示,则 ,1,0的大小顺序是( ) A、 B、 C、 D、 且1和 的大小无法确定14. 点A、B在数轴上的位置如图所示,其对应的数分别是和。对于以下结论:甲:;乙:;丙:;丁:。其中正确的是( )
A、 B、 C、 D、 且1和 的大小无法确定14. 点A、B在数轴上的位置如图所示,其对应的数分别是和。对于以下结论:甲:;乙:;丙:;丁:。其中正确的是( )
 A、甲、乙 B、甲、丙 C、乙、丁 D、丙、丁15. 在数轴上表示下列各数,并用“<”号把它们按照从小到大的顺序排列.
A、甲、乙 B、甲、丙 C、乙、丁 D、丙、丁15. 在数轴上表示下列各数,并用“<”号把它们按照从小到大的顺序排列.1.5,﹣(﹣1)100 , ﹣(﹣2),﹣22 , ﹣|﹣2|.
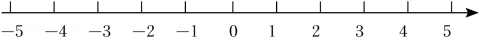
四、绝对值非负性的应用
-
16. 若|x﹣2|+2|y+3|+3|z﹣5|=0.
计算:
(1)、x,y,z的值.(2)、求|x|+|y|﹣|z|的值.17.(1)、已知有理数 , , 且ab<0,求a﹣b的值.(2)、已知有理数a,b,c满足 , 求a+b﹣c的值.18. 请根据图示的对话解答下列问题. (1)、 , .(2)、已知 , 求的值.19. 对于含绝对值的算式,在有些情况下,可以不需要计算出结果也能将绝对值符号去掉,例如:|7-6|=7-6;|6-7|=7-6;; .
(1)、 , .(2)、已知 , 求的值.19. 对于含绝对值的算式,在有些情况下,可以不需要计算出结果也能将绝对值符号去掉,例如:|7-6|=7-6;|6-7|=7-6;; .观察上述式子的特征,解答下列问题:
(1)、把下列各式写成去掉绝对值符号的形式(不用写出计算结果):①|23-47|=;②=;
(2)、当a>b时,|a-b|=;当a<b时,|a-b|=;(3)、计算: .20. 已知点A在数轴上对应的数为 , 点B在数轴上对应的数为b=2,A,B之间的距离记为或 , 请回答问题: (1)、设点P在数轴上对应的数为x,若 , 则x=_ .(2)、如图,点M,N,P是数轴上的三点,点M表示的数为4,点N表示的数为 ,动点P表示的数为x.
(1)、设点P在数轴上对应的数为x,若 , 则x=_ .(2)、如图,点M,N,P是数轴上的三点,点M表示的数为4,点N表示的数为 ,动点P表示的数为x.①若点P在点M、N之间,则 ▲ ;
②若 , 则x= ▲ .
③若点P表示的数是-5,现在有一蚂蚁从点P出发,以每秒1个单位长度的速度向右运动,当经过多少秒时,蚂蚁所在的点到点M、点N的距离之和是8?
五、绝对值化简求值
-
21. 已知 , 为实数,下列说法:①若 , 且 , 互为相反数,则;②若 , 则;③若 , 且 , 则;④若 , , 则;⑤若 , 则 , 其中正确个数为A、1 B、2 C、3 D、422. 有理数a,b,c在数轴上对应的点的位置如图所示,其中 , 则下列各式:①;②;③;④ , 正确的有( )
 A、4个 B、3个 C、2个 D、1个23. 已知ab0,则++的值是( )A、3 B、-3 C、3或-1 D、3或-324. 若xyz<0,则 的值为25. 有理数a,b在数轴上的位置如下图所示,在下列结论中∶①ab<0;②a+b>0;③a3>b2;④(a-b)3<0;⑤a<-b<b<-a;⑥|b-a|-|a|=b.正确的结论有( )
A、4个 B、3个 C、2个 D、1个23. 已知ab0,则++的值是( )A、3 B、-3 C、3或-1 D、3或-324. 若xyz<0,则 的值为25. 有理数a,b在数轴上的位置如下图所示,在下列结论中∶①ab<0;②a+b>0;③a3>b2;④(a-b)3<0;⑤a<-b<b<-a;⑥|b-a|-|a|=b.正确的结论有( ) A、5个 B、4个 C、3个 D、2个26. 已知非零有理数a,b,c满足 , .(1)、求 的值;(2)、若 ,求 的值.
A、5个 B、4个 C、3个 D、2个26. 已知非零有理数a,b,c满足 , .(1)、求 的值;(2)、若 ,求 的值.六、有理数的混合运算
-
27. 已知a、b互为相反数,e的绝对值为 , m与n互为倒数,则的值为( )A、1 B、3 C、0 D、无法确定28. 数学老师规定了一种新运算:若 , 是有理数,则 , 请你计算:;.29. 计算:.30. 用“*”定义一种新运算:对于任意有理数a和b,规定a*b=ab2+2ab+a.
如:1*3=1×32+2×1×3+1=16
(1)、求2*(﹣2)的值;(2)、若2*x=m, (其中x为有理数),试比较m,n的大小;(3)、若[ ] =a+4,求a的值.31. 定义:对于任意的有理数a,b(a≠b),a⊕b=(|a-b|+a+b)(1)、探究性质:①例:3⊕2=;2⊕3=;(-3)⊕2=;(-3)⊕(-2)=;
②可以再举几个例子试试,你有什么发现吗?请用含a,b的式子表示出a⊕b的一般规律;
(2)、性质应用:①运用发现的规律求[(-92.5)⊕16.33]⊕[(-33.8)⊕(-4)]的值;
②将-11,-10,-9,-8……,7,8这20个连续的整数,任意分为10组,每组两个数,现将每组的两个数中任一数值记作a,另一个记作b,求出a⊕b,10组数代入后可求得10个a⊕b的值,则这10个值的和的最小值是_▲_ .
32. 九宫格起源于中国古代的神秘图案河图和洛书.如图,将 , , , , , , , , 填入九宫格内,使每行、每列、每条对角线上三个数的和都相等,则的值为( )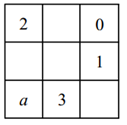 A、 B、 C、 D、33. 定义一种新的运算“”:
A、 B、 C、 D、33. 定义一种新的运算“”:;
;
;
;
;
;
;
;
;
;
(1)、仔细观察,归纳“”运算法则:两数进行“”运算时,;特别地,0与任何数进行“”运算,或任何数与0进行“”运算,结果为;
(2)、计算:;(3)、已知 , , , 试判断的值是否大于0?并说明理由.34. 规定:求若干个相同的不为零的有理数的除法运算叫做除方.如 , .类比有理数的乘方,我们把记作 , 读作“2的星3次方”;把记作 , 读作“的星4次方”.
一般地,把记作(其中, , , 为整数),读作“的星次方”.
(1)、直接写出计算结果: , , ;(2)、结合(1)中的运算,尝试把有理数的除方运算转化为乘方运算,可以归纳如下:一个非零有理数的星 , 为整数)次方等于 (从以下四个选项中选择最合适的一个,填写序号即可).
①这个数的相反数的次方;
②这个数的绝对值的次方;
③这个数的倒数的次方;
④这个数的次方.
(3)、关于“除方”运算,下列说法错误的是____ ;A、任何非零有理数的星3次方都等于它的倒数; B、对于任何不小于3正整数 , ; C、; D、负数的星5次方的结果是负数,负数的星6次方的结果是正数.(4)、结合上述探究结果,计算下式的值..
七、倒数的应用
-
35. 的倒数是( )A、 B、 C、-2022 D、202236. 5的相反数的倒数是( )A、-5 B、5 C、 D、37. 有理数a≠1,我们把称为a的差倒数,如:2的差倒数是=-1,-1的差倒数是.如果a1=3,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推。(1)、填空:a2= , a3=。(2)、试探寻规律,找出a2015的值38. 数学老师布置了一道思考题“计算:”,小明仔细思考了一番,用了一种不同的方法解决了这个问题:
原式的倒数为
所以
(1)、请你通过计算验证小明的解法的正确性:(2)、由此可以得到结论:一个数的倒数的倒数等于;(3)、请你运用小明的解法计算。八、科学计数法
-
39. 近年来,我国研发的北斗芯片实现了22纳米制程的突破,22纳米等于0.000000022米.用科学记数法表示0.000000022是 .40. 神舟十六号前往中国空间站后,组合体的在轨质量将超过吨(千克),堪称中国载人航天的历史性时刻,数据用科学记数法表示为( )A、 B、 C、 D、41. 全民义务植树在中华大地蓬勃展开.去年全国适龄公民累计17500000000人次参加义务植树,数据“17500000000”用科学记数法表示为( )A、 B、 C、 D、42. 北京时间2022年11月21日0点,万众瞩目的卡塔尔世界杯全面打响,据统计在小组赛的赛程中,场均观看直播人数达到了7062万人,则7062万用科学记数法表示为( )A、 B、 C、 D、
九、有理数的应用
-
43. 下列说法不正确的是:( )
① a一定是正数; ②0的倒数是0 ; ③最大的负整数是-1;④只有负数的绝对值是它的相反数; ⑤倒数等于本身的有理数只有1
A、①②③④ B、①③④⑤ C、①②④⑤ D、②③④⑤