四川省绵阳市涪城区2023-2024学年八年级上学期开学考试数学试卷
试卷更新日期:2023-09-19 类型:开学考试
一、填空题
-
1. 下列说法错误的是( )A、5是25的算术平方根 B、(-4)3的立方根是-4 C、无理数都是无限小数 D、 的平方根是2. 下列命题是真命题的是 ( )A、和为180°的两个角是邻补角 B、一条直线的垂线有且只有一条 C、点到直线的距离是指这一点到直线的垂线段 D、两条直线被第三条直线所截,若内错角相等,则同位角必相等3. 若m>n,则下列各式中正确的是 ( )A、m-5<n-5 B、m+5<n+5 C、6m<6n D、-2m<-2n4. 若关于x的不等式组的整数解共有三个,则a的取值范围是( ).A、 B、 C、 D、5. 已知AB∥CD,将一副直角三角板如图摆放,∠GEF=60°,∠MNP=45°.下列结论:①GE∥MP;②∠EFN=150°;③∠BEF=75°;④∠AEG=∠PNM.其中正确的个数是 ( )
 A、1 B、2 C、3 D、46. 2021年3月12日北京市统计局发布了《北京市2020年国民经济和社会发展统计公报》,其中列举了2020年北京市居民人均可支配收入.下面是小明同学根据2016—2020年北京市居民人均可支配收入绘制的统计图.
A、1 B、2 C、3 D、46. 2021年3月12日北京市统计局发布了《北京市2020年国民经济和社会发展统计公报》,其中列举了2020年北京市居民人均可支配收入.下面是小明同学根据2016—2020年北京市居民人均可支配收入绘制的统计图.
根据统计图提供的信息,下面四个说法中正确的是 ( )
A、2020年北京市居民人均可支配收入比2016年增加了16 004元 B、2017—2020年北京市居民人均可支配收入有增有减 C、2017年北京市居民人均可支配收入的增长率约为8.9% D、2017—2020年北京市居民人均可支配收入增长率最大的年份是2 020年7. 如图,一束光线先后经平面镜 , 反射后,反射光线与平行,当时,的度数为( )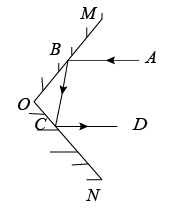 A、 B、 C、 D、8. 不等式组 的解集在数轴上表示正确的是( )A、
A、 B、 C、 D、8. 不等式组 的解集在数轴上表示正确的是( )A、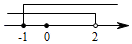 B、
B、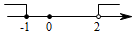 C、
C、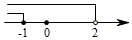 D、
D、 9. 如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠CDO=50°,则下列结论:①OG⊥AB;②OF平分∠BOD;③∠AOE=65°;④∠GOE=∠DOF,其中正确的有 ( )
9. 如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠CDO=50°,则下列结论:①OG⊥AB;②OF平分∠BOD;③∠AOE=65°;④∠GOE=∠DOF,其中正确的有 ( ) A、1个 B、2个 C、3个 D、4个10. 如图,图1是AD∥BC的一张纸条,按图1→图2→图3的顺序,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则∠AEF的度数为 ( )
A、1个 B、2个 C、3个 D、4个10. 如图,图1是AD∥BC的一张纸条,按图1→图2→图3的顺序,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则∠AEF的度数为 ( ) A、120° B、108° C、126° D、114°11. 2020年11月1日零时,我国开展第七次全国人口普查.2021年5月11日,国务院新闻办公室公布普查结果,如图是根据我国历次人口普查数据,绘制的我国每10万人中拥有大学文化(指大专及以上)程度人数的折线图.设2020年每10万人中拥有大学文化程度的人数与2010年相比的增长率为x,则下列关于x的方程正确的是 ( )
A、120° B、108° C、126° D、114°11. 2020年11月1日零时,我国开展第七次全国人口普查.2021年5月11日,国务院新闻办公室公布普查结果,如图是根据我国历次人口普查数据,绘制的我国每10万人中拥有大学文化(指大专及以上)程度人数的折线图.设2020年每10万人中拥有大学文化程度的人数与2010年相比的增长率为x,则下列关于x的方程正确的是 ( )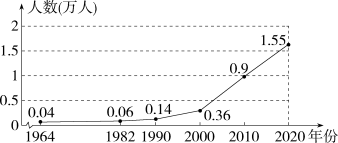 A、(1+0.9)x=1.55 B、0.9(1+x)×10=1.55 C、0.9(1+x)=1.55 D、0.9(1+x)10=1.5512. 小梦在某购物平台上购买甲、乙、丙三种商品,当购物车内选择3件甲,2件乙,1件丙时显示的价格为420元;当购物车内选择2件甲,3件乙,4件丙时显示的价格为580元,那么购买甲、乙、丙各两件应该付款 ( )A、200元 B、400元 C、500元 D、600元
A、(1+0.9)x=1.55 B、0.9(1+x)×10=1.55 C、0.9(1+x)=1.55 D、0.9(1+x)10=1.5512. 小梦在某购物平台上购买甲、乙、丙三种商品,当购物车内选择3件甲,2件乙,1件丙时显示的价格为420元;当购物车内选择2件甲,3件乙,4件丙时显示的价格为580元,那么购买甲、乙、丙各两件应该付款 ( )A、200元 B、400元 C、500元 D、600元二、填空题
-
13. 若点P(3a-6,1-a)在x轴上,则点P的坐标为.14. 如图,点A、B分别在x轴和y轴上,OA=1,OB=2,若将线段AB平移至A'B'的位置,则a+b的值为.
 15. 如图,已知AB∥EF,若α=∠A+∠F,β=∠B+∠C+∠D+∠E,则α与β之间的数量关系为.
15. 如图,已知AB∥EF,若α=∠A+∠F,β=∠B+∠C+∠D+∠E,则α与β之间的数量关系为. 16. 已知:y= , 当a,b取不同的值时,y也有不同的值,当y最小时,ba的算术平方根为.17. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(‘两’为我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹x两,牛每头y两,根据题意可列方程组为.
16. 已知:y= , 当a,b取不同的值时,y也有不同的值,当y最小时,ba的算术平方根为.17. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(‘两’为我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹x两,牛每头y两,根据题意可列方程组为.三、解答题
-
18. 解不等式(组):(1)、(2)、19. nbsp;. 如图,将三角形ABC向左平移3个单位长度,再向下平移4个单位长度,得到三角形A1B1C1.
 (1)、画出三角形A1B1C1 , 并写出A1、B1、C1的坐标;(2)、已知三角形ABC内部一点P的坐标为(a,b),若点P随三角形ABC一起平移,平移后点P的对应点P1的坐标为(-2,-2),则a= , b=;(3)、求三角形ABC的面积.20. 已知关于x,y的二元一次方程组且x+y<0.(1)、试用含m的式子表示方程组的解;(2)、求实数m的取值范围;(3)、化简:|m+-m|.21. 如图①,已知直线AB、CD分别与直线EF相交于M、N两点,∠BME=50°.
(1)、画出三角形A1B1C1 , 并写出A1、B1、C1的坐标;(2)、已知三角形ABC内部一点P的坐标为(a,b),若点P随三角形ABC一起平移,平移后点P的对应点P1的坐标为(-2,-2),则a= , b=;(3)、求三角形ABC的面积.20. 已知关于x,y的二元一次方程组且x+y<0.(1)、试用含m的式子表示方程组的解;(2)、求实数m的取值范围;(3)、化简:|m+-m|.21. 如图①,已知直线AB、CD分别与直线EF相交于M、N两点,∠BME=50°. (1)、请添加一个条件,使直线AB∥CD,并说明理由;(2)、如图②,在(1)的条件下,作∠MND的平分线交AB于点G,求∠BGN的度数.22.
(1)、请添加一个条件,使直线AB∥CD,并说明理由;(2)、如图②,在(1)的条件下,作∠MND的平分线交AB于点G,求∠BGN的度数.22.
 (1)、已知AB∥CD,点M为平面内一点.如图①,BM⊥CM,小颖说过点M作MP∥AB,很容易说明∠ABM和∠DCM互余.请你帮小颖写出具体的证明过程.(2)、如图②,AB∥CD,点M在射线ED上运动,当点M移动到点A与点D之间时,试判断∠BMC与∠ABM,∠DCM的数量关系,并说明理由.(3)、在(2)的条件下,当点M在射线ED上的其他地方运动时(点M与E,A,D三点不重合),请直接写出∠BMC与∠ABM,∠DCM之间的数量关系.
(1)、已知AB∥CD,点M为平面内一点.如图①,BM⊥CM,小颖说过点M作MP∥AB,很容易说明∠ABM和∠DCM互余.请你帮小颖写出具体的证明过程.(2)、如图②,AB∥CD,点M在射线ED上运动,当点M移动到点A与点D之间时,试判断∠BMC与∠ABM,∠DCM的数量关系,并说明理由.(3)、在(2)的条件下,当点M在射线ED上的其他地方运动时(点M与E,A,D三点不重合),请直接写出∠BMC与∠ABM,∠DCM之间的数量关系.