【B卷】第一章 直角三角形的边角关系—北师大版九年级下册单元测试
试卷更新日期:2023-09-17 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如图,△ABC的三个顶点都在正方形网格的格点上,则sin∠A的值为( )
 A、 B、 C、 D、2. 如图,△ABC是锐角三角形,sinC= ,则sinA的取值范围是( )
A、 B、 C、 D、2. 如图,△ABC是锐角三角形,sinC= ,则sinA的取值范围是( ) A、0 B、 C、 D、3. 下列计算中错误的是( )A、 B、 C、 D、4. 如图,与 , , 分别交于点E,G,F,且 , , 则下列结论错误的是( )
A、0 B、 C、 D、3. 下列计算中错误的是( )A、 B、 C、 D、4. 如图,与 , , 分别交于点E,G,F,且 , , 则下列结论错误的是( ) A、 B、 C、 D、5. 如图,以矩形OABC的两边OA和OC所在直线为x轴、y轴建立平面直角坐标系。将矩形OABC绕点O逆时针旋转30°,得到矩形ODEF,若当点A的坐标为(- , 0)时,反比例函数的图象恰好经过B、F两点,则此时k的值为( ).
A、 B、 C、 D、5. 如图,以矩形OABC的两边OA和OC所在直线为x轴、y轴建立平面直角坐标系。将矩形OABC绕点O逆时针旋转30°,得到矩形ODEF,若当点A的坐标为(- , 0)时,反比例函数的图象恰好经过B、F两点,则此时k的值为( ).
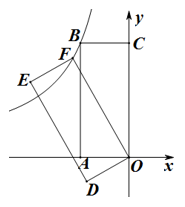
A、 B、-6 C、 D、-36. 如图所示,在中,按以下步骤作图:①连接 , 以点C为圆心,以长为半径作弧,交于点F;②分别以点D,F为圆心,以长为半径作弧,两弧相交于点G;③作射线交于点E.若 , , 则的长为( ) A、4 B、 C、 D、7. 如图,矩形的对角线相交于点O, , 分别过点D,点C作的平行线,两线相交于点E,连接交于点F,则的值是( )
A、4 B、 C、 D、7. 如图,矩形的对角线相交于点O, , 分别过点D,点C作的平行线,两线相交于点E,连接交于点F,则的值是( )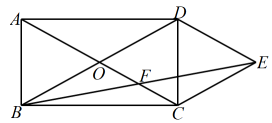 A、7 B、 C、8 D、8. 如图,小明在处看到西北方向上有一凉亭 , 北偏东的方向上有一棵大树 , 已知凉亭在大树的正西方向,若米,则、两点相距为( )米.
A、7 B、 C、8 D、8. 如图,小明在处看到西北方向上有一凉亭 , 北偏东的方向上有一棵大树 , 已知凉亭在大树的正西方向,若米,则、两点相距为( )米. A、 B、 C、 D、9. 如图,为测量一条河的宽度,分别在河岸一边相距a米的A、B两点处,观测对岸的标志物P,测得、 , 那么这条河的宽度是( )
A、 B、 C、 D、9. 如图,为测量一条河的宽度,分别在河岸一边相距a米的A、B两点处,观测对岸的标志物P,测得、 , 那么这条河的宽度是( ) A、米 B、米 C、米 D、米10. 如图,小华站在水库的堤坝上的G点,看见水库里有一小船沿垂直于岸边的方向划过来.此时,测得小船C的俯角 ,若小华的眼睛与底面的距离 米, 米. 平行于 所在的直线,迎水坡 的坡度 : ,坡长 为 米,点A,B,C,D、F、G在同一平面内,则此时小船C到岸边的距离 的长为( )米 ,结果精确到 米
A、米 B、米 C、米 D、米10. 如图,小华站在水库的堤坝上的G点,看见水库里有一小船沿垂直于岸边的方向划过来.此时,测得小船C的俯角 ,若小华的眼睛与底面的距离 米, 米. 平行于 所在的直线,迎水坡 的坡度 : ,坡长 为 米,点A,B,C,D、F、G在同一平面内,则此时小船C到岸边的距离 的长为( )米 ,结果精确到 米 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共15分)
-
11. 如图,在中,对角线交于点O.点M是边的中点,连接 , 作.已知平分 , 平分 , 若 , 则的值为.
 12. 如图,在正方形内部作等边 , 交于F点,过E作 , 分别交于点G,H.则的值是 .
12. 如图,在正方形内部作等边 , 交于F点,过E作 , 分别交于点G,H.则的值是 . 13. 矩形的边 . 点为平面内一点, , 若 , 则 .14. 如图,在矩形中,点E为上一点, , , 连接 , 将沿所在的直线翻折,得到 , 交于点F,将沿所在的直线翻折,得到 , 交于点G,的值为 .
13. 矩形的边 . 点为平面内一点, , 若 , 则 .14. 如图,在矩形中,点E为上一点, , , 连接 , 将沿所在的直线翻折,得到 , 交于点F,将沿所在的直线翻折,得到 , 交于点G,的值为 . 15. 图1是一辆卸货车实物图, 折线ABC是支架, B D为可伸缩的液压支撑杆, 测得 , 图2是卸货车不工作时的侧面示意图,此时AB与FG在同一直线上,
15. 图1是一辆卸货车实物图, 折线ABC是支架, B D为可伸缩的液压支撑杆, 测得 , 图2是卸货车不工作时的侧面示意图,此时AB与FG在同一直线上,
CDll AB,且∠DEF=135°,则BF= , 图3是卸货车工作时的侧面示意图,折线CDE可绕点C上下旋转,且∠CDE始终保持不变,EF始终保持与地面垂直,当BD⊥DE时,FG与AB的距离为.


三、解答题(共7题,共55分)
-
16. 如图,已知正方形 , 、分别为边、的中点,与交于点 , , 垂足为点 .
 (1)、求证:;(2)、连接 , 求正弦值.17. 如图,在菱形中, , 是对角线上一点.是线段延长线上一点,且 , 连接 .
(1)、求证:;(2)、连接 , 求正弦值.17. 如图,在菱形中, , 是对角线上一点.是线段延长线上一点,且 , 连接 . (1)、如图1,若是线段上任意一点,连接 , 求证: .(2)、在第(1)题的前提下,求证: .(3)、如图2,若是线段延长线上一点,其他条件不变,且 , 求的值.18. 图1是某浴室花洒实景图,图2是该花洒的侧面示意图.已知活动调节点B可以上下调整高度,离地面CD的距离BC=160cm.设花洒臂与墙面的夹角为α,可以扭动花洒臂调整角度,且花洒臂长AB=30cm.假设水柱AE垂直AB直线喷射,小华在离墙面距离CD=120cm处淋浴.
(1)、如图1,若是线段上任意一点,连接 , 求证: .(2)、在第(1)题的前提下,求证: .(3)、如图2,若是线段延长线上一点,其他条件不变,且 , 求的值.18. 图1是某浴室花洒实景图,图2是该花洒的侧面示意图.已知活动调节点B可以上下调整高度,离地面CD的距离BC=160cm.设花洒臂与墙面的夹角为α,可以扭动花洒臂调整角度,且花洒臂长AB=30cm.假设水柱AE垂直AB直线喷射,小华在离墙面距离CD=120cm处淋浴.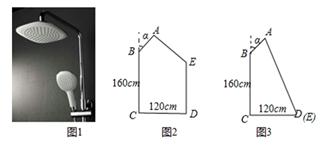 (1)、当α=30°时,水柱正好落在小华的头顶上,求小华的身高DE.(2)、如果小华要洗脚,需要调整水柱AE,使点E与点D重合,调整的方式有两种:
(1)、当α=30°时,水柱正好落在小华的头顶上,求小华的身高DE.(2)、如果小华要洗脚,需要调整水柱AE,使点E与点D重合,调整的方式有两种:①其他条件不变,只要把活动调节点B向下移动即可,移动的距离BF与小华的身高DE有什么数量关系?直接写出你的结论;
②活动调节点B不动,只要调整α的大小,在图3中,试求α的度数.
(参考数据: ≈1.73,sin8.6°≈0.15,sin36.9°≈0.60,tan36.9°≈0.75)
19. 如图1,某学校开展“交通安全日”活动.在活动中,交警叔叔向同学们展示了大货车盲区的分布情况,并提醒大家:坐在驾驶室的司机根本看不到在盲区中的同学们,所以一定要远离大货车的盲区,保护自身安全.小刚所在的学习小组为了更好的分析大货车盲区的问题,将图1用平面图形进行表示,并标注了测量出的数据,如图2.在图2中大货车的形状为矩形,而盲区1为梯形,盲区2、盲区3为直角三角形,盲区4为正方形.
请你帮助小刚的学习小组解决下面的问题:
(1)、盲区1的面积约是m2;盲区2的面积约是m2;(≈1.4,≈1.7,sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,结果保留整数)(2)、如果以大货车的中心A点为圆心,覆盖所有盲区的半径最小的圆为大货车的危险区域,请在图2中画出大货车的危险区域.20. 为了美化环境,提高民众的生活质量,市政府在三角形花园边上修建一个四边形人工湖泊 , 并沿湖泊修建了人行步道.如图,点在点的正东方向170米处,点在点的正北方向,点都在点的正北方向,长为100米,点在点的北偏东方向,点在点的北偏东方向. (1)、求步道的长度.(2)、点处有一个小商店,某人从点出发沿人行步道去商店购物,可以经点到达点 , 也可以经点到达点 , 请通过计算说明他走哪条路较近.结果精确到个位)(参考数据:)21. 综合与实践如图,正方形与正方形有公共顶点C, , , 连接 .
(1)、求步道的长度.(2)、点处有一个小商店,某人从点出发沿人行步道去商店购物,可以经点到达点 , 也可以经点到达点 , 请通过计算说明他走哪条路较近.结果精确到个位)(参考数据:)21. 综合与实践如图,正方形与正方形有公共顶点C, , , 连接 .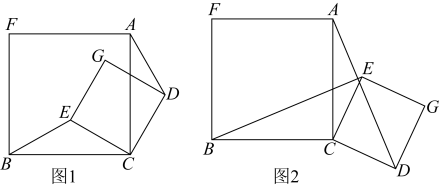 (1)、如图①,当点E,G在正方形内时,线段与的数量关系是 , 位置关系是;(2)、把正方形绕点C旋转到如图②的位置,(1)中的结论还成立吗?说明理由;(3)、把正方形绕点C在平面内自由旋转.
(1)、如图①,当点E,G在正方形内时,线段与的数量关系是 , 位置关系是;(2)、把正方形绕点C旋转到如图②的位置,(1)中的结论还成立吗?说明理由;(3)、把正方形绕点C在平面内自由旋转.①当A,E,D三点在同一条直线上时,AE的长是;
②旋转过程中,的最大值为 .
22. 如图 (1)、(问题情境)
(1)、(问题情境)如图1,在矩形ABCD中,将矩形沿AC折叠,点B落在点E处,设AD与CE相交于点F,那么AC与DE的位置关系为.
(2)、(类比探究)如图2,若四边形ABCD为平行四边形,上述“问题情境”中的条件不变,
①猜想AC与DE的位置关系,并证明你的结论;
②当∠B与∠ACB满足什么数量关系时,△ABC∽△FEA?请说明理由;
(3)、(拓展应用)如图3,▱ABCD中,∠B=60°,AB=6,上述“问题情境”中的条件不变,当△AEC是直角三角形时,请直接写出DE的长为.