【A卷】第一章 直角三角形的边角关系—北师大版九年级下册单元测试
试卷更新日期:2023-09-17 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如图,在中, , , , 则等于( )
 A、 B、 C、 D、2. 已知角α为ABC的内角,且cosα= , 则α的取值范围是( )A、0°<α<30° B、30°<α<45° C、45°<α<60° D、60°<α<90°3. 已知sin42°≈ , 则cos48°的值约为( )A、 B、 C、 D、4. 的值等于( )A、 B、 C、1 D、25. 已知 ,用计算器求∠A的大小,下列按键顺序正确的是( )
A、 B、 C、 D、2. 已知角α为ABC的内角,且cosα= , 则α的取值范围是( )A、0°<α<30° B、30°<α<45° C、45°<α<60° D、60°<α<90°3. 已知sin42°≈ , 则cos48°的值约为( )A、 B、 C、 D、4. 的值等于( )A、 B、 C、1 D、25. 已知 ,用计算器求∠A的大小,下列按键顺序正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 如图,矩形的对角线相交于点 . 若 , 则( )
6. 如图,矩形的对角线相交于点 . 若 , 则( )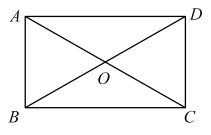 A、 B、 C、 D、7. 在中, , , 若是锐角三角形,则满足条件的长可以是( )A、1 B、2 C、6 D、88. 如图,在中, , 设所对的边边长分别为a,b,c,则下列等式正确的是( )
A、 B、 C、 D、7. 在中, , , 若是锐角三角形,则满足条件的长可以是( )A、1 B、2 C、6 D、88. 如图,在中, , 设所对的边边长分别为a,b,c,则下列等式正确的是( )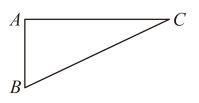 A、 B、 C、 D、9. 如图,海中有一小岛 , 在点测得小岛在北偏东方向上,渔船从点出发由西向东航行到达点,在点测得小岛恰好在正北方向上,此时渔船与小岛的距离为 . ( )
A、 B、 C、 D、9. 如图,海中有一小岛 , 在点测得小岛在北偏东方向上,渔船从点出发由西向东航行到达点,在点测得小岛恰好在正北方向上,此时渔船与小岛的距离为 . ( )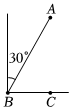 A、 B、 C、 D、10. 学校开放日即将来临,负责布置的林老师打算从学校图书馆的顶楼拉出一条彩旗绳到地面,如图所示.已彩旗绳与地面形成角(即)、彩旗绳固定在地面的位置与图书馆相距32米(即米),则彩旗绳的长度为( )
A、 B、 C、 D、10. 学校开放日即将来临,负责布置的林老师打算从学校图书馆的顶楼拉出一条彩旗绳到地面,如图所示.已彩旗绳与地面形成角(即)、彩旗绳固定在地面的位置与图书馆相距32米(即米),则彩旗绳的长度为( )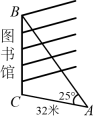 A、米 B、米 C、米 D、米
A、米 B、米 C、米 D、米二、填空题(每题3分,共15分)
-
11. 计算:12. 如图,的顶点都是边长为1的小正方形组成的网格的格点,则的正切值为 .
 13. 在中, , , 则 .14. 如图,在中, , 点D在边AB上,连接CD . 若 , , 则 .
13. 在中, , , 则 .14. 如图,在中, , 点D在边AB上,连接CD . 若 , , 则 .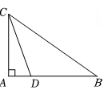 15. 如图,斜坡的坡度 , 现需要在不改变坡高的情况下将坡度变缓,调整后的斜坡的坡度 , 已知斜坡米,那么斜坡米.
15. 如图,斜坡的坡度 , 现需要在不改变坡高的情况下将坡度变缓,调整后的斜坡的坡度 , 已知斜坡米,那么斜坡米.
三、解答题(共7题,共55分)
-
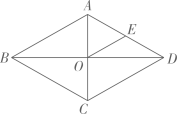
16. 计算:17. 如图,菱形的对角线相交于点为的中点, , .求的长及的值.
 18. 如图,某海域有一小岛P,一艘轮船在A处测得小岛P位于北偏东60°的方向上,当轮船自西向东航行12海里到达B处,在B处测得小岛P位于北偏东30°方向上,若以点P为圆心,半径为10海里的圆形海域内有暗礁,那么轮船由B处继续向东航行是否有触礁危险?请说明理由.(参考数据:).
18. 如图,某海域有一小岛P,一艘轮船在A处测得小岛P位于北偏东60°的方向上,当轮船自西向东航行12海里到达B处,在B处测得小岛P位于北偏东30°方向上,若以点P为圆心,半径为10海里的圆形海域内有暗礁,那么轮船由B处继续向东航行是否有触礁危险?请说明理由.(参考数据:). 19. 教室里的投影仪投影时,可以把投影光线CA,CB及在黑板上的投影图像高度AB抽象成如图所示的△ABC, . 黑板上投影图像的高度 , CB与AB的夹角 , 求AC的长.(结果精确到1cm.参考数据: , , )
19. 教室里的投影仪投影时,可以把投影光线CA,CB及在黑板上的投影图像高度AB抽象成如图所示的△ABC, . 黑板上投影图像的高度 , CB与AB的夹角 , 求AC的长.(结果精确到1cm.参考数据: , , )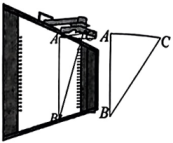 20. 如图,AD、AE分别是△ABC边BC上的高和中线,已知 , ∠C=45°.
20. 如图,AD、AE分别是△ABC边BC上的高和中线,已知 , ∠C=45°. (1)、求AD的长;(2)、求sin∠BAE的值.21. 如图,已知∠ABC和射线BD上一点P(点P与点B不重合),且点P到BA、BC的距离为PE、PF.
(1)、求AD的长;(2)、求sin∠BAE的值.21. 如图,已知∠ABC和射线BD上一点P(点P与点B不重合),且点P到BA、BC的距离为PE、PF. (1)、若∠EBP=40°,∠FBP=20°,PB=m,试比较PE、PF的大小;(2)、若∠EBP=α,∠FBP=β,α,β都是锐角,且α>β.试判断PE、PF的大小,并给出证明.22. 小明同学在学习了解直角三角形及其应用的知识后,尝试利用所学测量大树的高度,如图,于点B,在C处测得大树顶端A的仰角为 , 再从点C出发沿斜坡前进10米到达D处,测得大树顶端A的仰角为 , 测得山坡脚C处的俯角为(图中各点均在同一平面内,点E,C,B在同一水平线上).
(1)、若∠EBP=40°,∠FBP=20°,PB=m,试比较PE、PF的大小;(2)、若∠EBP=α,∠FBP=β,α,β都是锐角,且α>β.试判断PE、PF的大小,并给出证明.22. 小明同学在学习了解直角三角形及其应用的知识后,尝试利用所学测量大树的高度,如图,于点B,在C处测得大树顶端A的仰角为 , 再从点C出发沿斜坡前进10米到达D处,测得大树顶端A的仰角为 , 测得山坡脚C处的俯角为(图中各点均在同一平面内,点E,C,B在同一水平线上). (1)、求小明从点C到达点D的过程中上升的高度是多少;(2)、求这棵大树的高度(结果取整数).(参考数据: , )
(1)、求小明从点C到达点D的过程中上升的高度是多少;(2)、求这棵大树的高度(结果取整数).(参考数据: , )