【提升卷】2.5二次函数与一元二次方程—2023-2024学年北师大版九年级下册同步测试

试卷更新日期：2023-09-17 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 已知二次函数 $y ＝ x^{2} ＋ 3 x - m$ （m为常数）的图像与x轴的一个公共点为（1，0），则关于x的一元二次方程 $x^{2} ＋ 3 x - m ＝ 0$ 的两实数根是（　　）

A、 $x_{1} ＝ 1 ， x_{2} ＝ - 4$ B、 $x_{1} ＝ 1 ， x_{2} ＝ 2$ C、 $x_{1} ＝ 1 ， x_{2} ＝ - 3$ D、 $x_{1} ＝ 1 ， x_{2} ＝ 3$

查看试题解析
2. 已知二次函数 $y = a x^{2} + b x + c$ 的图象经过 $(- 3 ， 0)$ 与 $(1 ， 0)$ 两点，关于 $x$ 的方程 $a x^{2} + b x + c + m = 0$ $(m > 0)$ 有两个根，其中一个根是3．则关于 $x$ 的方程 $a x^{2} + b x + c + n = 0$ $(0 < n < m)$ 有两个整数根，这两个整数根是（）

A、 $- 2$ 或0 B、 $- 4$ 或2 C、 $- 5$ 或3 D、 $- 6$ 或4

查看试题解析
3. 二次函数y＝ax²+bx+c（a≠0）的部分图象如图，图象过点（﹣2，0），且对称轴为直线x＝1，下列结论正确的是（）

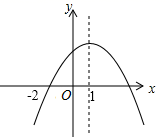A、abc＞0 B、关于x的一元二次方程ax²+bx+c＝0的两根为3和﹣2 C、9a+c＞3b D、当y＞0时，x的取值范围是﹣2＜x＜4

查看试题解析
4. 二次函数 $y = - x^{2} + m x$ 的图象如图，对称轴为直线 $x = 2$ ，关于 $x$ 的一元二次方程 $- x^{2} + m x - t = 0$ （ $t$ 为实数）在 $1 < x < 5$ 的范围内有解，则 $t$ 的取值范围是（）

A、 $t > - 5$ B、 $- 5 < t < 3$ C、 $3 < t \leq 4$ D、 $- 5 < t \leq 4$

查看试题解析
5. 如图，以直线 $x = 1$ 为对称轴的二次函数 $y = a x^{2} + b x + c$ 的图象与x轴负半轴交于A点，则一元二次方程 $a x^{2} + b x + c = 0$ 的正数解的范围是（）.

A、 $2 < x < 3$ B、 $3 < x < 4$ C、 $4 < x < 5$ D、 $5 < x < 6$

查看试题解析
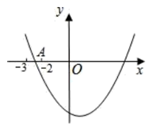6. 一元二次方程 $(x - 1) (x - 2) = 6$ 的两实根分别为 $s$ ， $t$ ，且 $s < t$ ，以下关系成立的是（）

A、 $s < 1$ 且 $t > 2$ B、 $1 < s < 2 < t$ C、 $s < 1 < t < 2$ D、 $1 < s < t < 2$

查看试题解析
7. 已知 $m > 0$ ，关于x的一元二次方程 $(x + 1) (x - 2) - m = 0$ 的解为 $x_{1} ， x_{2} (x_{1} < x_{2})$ ，则下列结论正确的是( 　)

A、 $x_{1} < - 1 < 2 < x_{2}$ B、 $- 1 < x_{1} < 2 < x_{2}$ C、 $- 1 < x_{1} < x_{2} < 2$ D、 $x_{1} < - 1 < x_{2} < 2$

查看试题解析
8. 设一元二次方程 $(x + 1) (x - 3) = a (a > 0)$ 的两实数根分别为 $α$ ， $β$ 且 $α < β$ ，则 $α$ 、 $β$ 满足（）

A、 $- 1 < α < β < 3$ B、 $α < - 1 < 3 < β$ C、 $α < - 1 < β < 3$ D、 $- 1 < α < 3 < β$

查看试题解析
9. “如果二次函数 $y = a x^{2} + b x + c$ 的图象与x轴有两个公共点，那么一元二次方程 $a x^{2} + b x + c = 0$ 有两个不相等的实数根．”请根据你对这句话的理解，解决下面问题：若m、 $n (m < n)$ 是关于x的方程 $1 - (x - a) (x - b) = 0$ 的两根，且 $0 < a < b$ ，则a、b、m、n的大小关系是（）

A、 $m < a < b < n$ B、 $a < m < n < b$ C、 $a < m < b < n$ D、 $m < a < n < b$

查看试题解析
10. 如图，已知关于x的一元二次方程 $a (x - k)^{2} - 1 = 0$ 的两根在数轴上对应的点分别在区域①和区域②，区域均含端点，则k的值可能是（）

A、-1 B、0 C、1 D、2

查看试题解析

二、填空题（每题3分，共15分）

11. 已知二次函数 $y ＝ - x^{2} + 2 x + m$ 的部分图象如图所示，则关于x的一元二次方程 $- x^{2} + 2 x + m ＝ 0$ 的解为 .

查看试题解析
12. 如图，抛物线 $y = a x^{2} + b x + c (a < 0)$ 的对称轴是直线 $x = - 1$ ，与x轴的一个交点为 $(- 5 ， 0)$ ，若关于x的一元二次方程 $a x^{2} + b x + c = 0$ 的两根为 $x_{1} ， x_{2} (x_{1} < x_{2})$ ，则 $x_{1} - x_{2}$ 的值为.

查看试题解析
13. 二次函数 $y = a x^{2} + b x$ 的图象如图，若一元二次方程 $a x^{2} + b x = m$ 有实数根，则 $m$ 的最小值为

查看试题解析

14. 二次函数

y = a x^{2} + b x + c

（a≠0，a，b，c是常数）中，自变量x与函数y的对应值如下表：

x	-1	- $\frac{1}{2}$	0	$\frac{1}{2}$	1	$\frac{3}{2}$	2	$\frac{5}{2}$	3
y	-2	$- \frac{1}{4}$	1	$\frac{7}{4}$	2	$\frac{7}{4}$	1	$- \frac{1}{4}$	-2

一元二次方程 $a x^{2} + b x + c = 0$ （a≠0，a，b，c是常数）的两个根 $x_{1} ， x_{2}$ 的取值范围是下列选项中的哪一个（填序号）

① $- \frac{1}{2} < x_{1} < 0 ， \frac{3}{2} < x_{2} < 2$ ② $- 1 < x_{1} < - \frac{1}{2} ， 2 < x_{2} < \frac{5}{2}$

③ $- \frac{1}{2} < x_{1} < 0 ， 2 < x_{2} < \frac{5}{2}$ ④ $- 1 < x_{1} < - \frac{1}{2} ， \frac{3}{2} < x_{2} < 2$

查看试题解析

15. 在平面直角坐标系中，抛物线 $y = a x^{2} - 4 a x - 1$ 经过点 $(2 ， 7)$ ．若关于 $x$ 的一元二次方程 $a x^{2} - 4 a x - 1 - t = 0$ （ $t$ 为实数）在 $\frac{1}{2} < x < 4$ 的范围内有实数根，则 $t$ 的取值范围为.

查看试题解析

三、解答题（共7题，共55分）

16. 已知关于 $x$ 的一元二次方程 $x^{2} - (2 m + 1) x + m (m + 1) = 0$ .

(1)、求证：无论 $m$ 取何值，方程总有两个不相等的实数根；

(2)、若此抛物线 $y = x^{2} - (2 m + 1) x + m (m + 1)$ 与直线 $y = x - 3 m$ 的一个交点在 $y$ 轴上，求 $m$ 的值.

查看试题解析
17. 已知关于 $x$ 的一元二次方程 $x^{2} + (k - 5) x + 1 - k = 0$ ，其中 $k$ 为常数.

(1)、求证：无论 $k$ 为何值，方程总有两个不相等实数根.

(2)、已知函数 $y = x^{2} + (k - 5) x + 1 - k$ 的图象不经过第三象限，求 $k$ 的取值范围.

查看试题解析
18. 已知抛物线 $y = 3 a x^{2} + 2 b x + c$ .

(1)、若 $a = b = 1$ ， $c = - 1$ ，求该抛物线与 $x$ 轴公共点的坐标；

(2)、若 $a = b = 1$ ，且当 $- 1 < x < 1$ 时，抛物线与x轴有且只有一个公共点，求 $c$ 的取值范围；

(3)、若 $a + b + c = 0$ ，且 $x_{1} = 0$ 时，对应的 $y_{1} > 0$ ； $x_{2} = 1$ 时，对应的 $y_{2} > 0$ ，试判断当 $0 < x < 1$ 时，抛物线与 $x$ 轴是否有公共点？若有，请证明你的结论；若没有，请说明理由.

查看试题解析

19. 某班“数学兴趣小组”对函数

y = x^{2} - 2 \sqrt{x^{2}} - 3

的图象和性质进行了探究，探究过程如下，请补充完整.

(1)、自变量

x

的取值范围是全体实数，

x

与

y

的几组对应值列表如下：

$x$	$\dots$	$- 3$	$- \frac{5}{2}$	$- 2$	$- 1$	$0$	$1$	$2$	$3$	$4$	$\dots$
$y$	$\dots$	$0$	$- \frac{7}{4}$	$m$	$- 4$	$- 3$	$- 4$	$- 3$	$- \frac{7}{4}$	$0$	$\dots$

其中， $m =$ .

(2)、根据上表数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请画出该图象的另一部分；

(3)、观察函数图象，写出两条函数的性质；

(4)、进一步探究函数图象发现：

①方程 $x^{2} - 2 \sqrt{x^{2}} - 3 = 0$ 有个实数根；

②函数图象与直线 $y = - 3$ 有个交点，所以对应方程 $x^{2} - 2 \sqrt{x^{2}} - 3 = - 3$ 有个实数根；

③关于 $x$ 的方程 $x^{2} - 2 \sqrt{x^{2}} - 3 = a$ 有 $4$ 个实数根， $a$ 的取值范围是.

查看试题解析

20. 我们知道，可以借助于函数图象求方程的近似解.如图（甲），把方程x﹣2＝1﹣x的解看成函数y＝x﹣2的图象与函数y＝1﹣x的图象的交点的横坐标，求得方程x﹣2＝1﹣x的解为x＝1.5.

(1)、如图（乙），已画出了反比例函数 $y = \frac{1}{x}$ 在第一象限内的图象，借助于此图象求出方程2x²﹣2x﹣1＝0的正数解.（要求画出相应函数的图象，结果精确到0.1）

(2)、选择：三次方程x³﹣x²﹣2x+1＝0的根的正负情况是　　.

A、有两个负根，一个正根 B、有三个负根 C、有一个负根，两个正根 D、有三个正根

查看试题解析
21. 我们不妨约定：若某函数图象上至少存在不同的两点关于原点对称，则把该函数称之为“D函数”，其图象上关于原点对称的两点叫做一对“D点”.根据该约定，完成下列各题：

(1)、在下列关于x的函数中，是“D函数”的，请在相应题目后面的括号中打“√”，不是“D函数”的打“×”.
① $y = 2 x$ （）；② $y = 3 x - 1$ （）；③ $y = (x - 1)^{2}$ （）；

(2)、若点 $A (1 ， m)$ 与点 $B (n ， - 4)$ 是关于x的“D函数” $y = a x^{2} + b x + c (a \neq 0)$ 的一对“D点”，且该函数的对称轴始终位于直线 $x = 1$ 的右侧，求a，b，c的值或取值范围；

(3)、若关于x的“D函数” $y = a x^{2} + 2 b x + 3 c$ （a，b，c是常数）同时满足下列两个条件：① $a + b + c = 0$ ；② $(2 c + b - a) (2 c + b + 3 a) < 0$ .求该“D函数”截x轴得到的线段长度的取值范围.

查看试题解析
22. 阅读与思考：下面是小明同学的数学小论文，请仔细阅读并完成相应的任务．
用函数观点认识一元二次方程根的情况

我们知道，一元二次方程ax²+bx+c=0(a≠0)的根就是相应的二次函数y=ax²+bx+c(a≠0)的图像(抛物线)与x轴交点的横坐标．抛物线与x轴的交点有三种情况：有两个交点、有一个交点、无交点与此相对应，一元二次方程的根也有三种情况：有两个不相等的实数根、有两个相等的实数根、无实数根．因此可用抛物线与x轴的交点个数确定一元二次方程根的情况．

下面根据抛物线的顶点坐标( $- \frac{b}{2 a}$ ， $\frac{4 a c - b^{2}}{4 a}$ ）和一元二次方程根的判别式△=b²-4ac，分a>0和a<0两种情况进行分析：
当a>0时，抛物线开口向上．

①当△=b²-4ac>0时，有4ac-b²<0．

∵a>0，∴顶点纵坐标 $\frac{4 a c - b^{2}}{4 a}$ <0，

∴顶点在x轴的下方，抛物线与x轴有两个交点(如图①)，

∴一元二次方程ax²+bx+c=0(a≠0)有两个不相等的实数根．

②当△=b²-4ac=0时，有4ac-b²=0．

∵a>0，∴顶点纵坐标 $\frac{4 a c - b^{2}}{4 a}$ =0，

∴顶点在x轴上，抛物线与x轴有一个交点(如图②)，

∴一元二次方程ax²+bx+c=0(a≠0)有两个相等的实数根，

③当△=b²-4ac<0……
当a<0时，抛物线开口向下．

……

任务：

(1)、上面小论文中的分析过程，主要运用的数学思想是(从下面选项中选出两个即可)
A．数形结合

B．统计思想

C．分类讨论

D．转化思想

(2)、请参照小论文中当a>0时①②的分析过程，写出③中当a>0，△<0时，一元二次方程根的情况的分析过程，并画出相应的示意图．

(3)、实际上，除一元二次方程外，初中数学还有一些知识也可以用函数观点来认识，例如：可用函数观点来认识一元一次方程的解，请你再举出一例．

查看试题解析