【培优卷】2.5二次函数与一元二次方程—2023-2024学年北师大版九年级下册同步测试

试卷更新日期：2023-09-17 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 抛物线 $y = - x^{2} + k x + k - \frac{5}{4}$ 与x轴的一个交点为 $A (m ， 0)$ ，若 $- 2 \leq m \leq 1$ ，则实数 $k$ 的取值范围是（）

A、 $- \frac{21}{4} \leq k \leq 1$ B、 $k \leq$ $- \frac{21}{4}$ 或 $k \geq 1$ C、 $- 5 \leq k \leq$ $\frac{9}{8}$ D、 $k \leq - 5$ 或 $k \geq$ $\frac{9}{8}$

查看试题解析
2. 如果二次函数y＝ax²＋bx＋c的图象与x轴有两个公共点，那么一元二次方程ax²＋bx＋c=0有两个不相等的实数根.”请根据你对这句话的理解，解决下面问题：若m、n（m＜ n）是关于x的方程1-（x-a）(x-b)=0的两根，且a＜ b，则a、b、m、n的大小关系是（）

A、a ＜ m＜ b＜ n B、a＜ m＜ n＜ b C、m ＜ a＜ b＜ n D、m＜ a＜ n＜ b

查看试题解析
3. 已知二次函数y=a（x-h）²+k（a≠0）的图象与一次函数y=mx+n（m≠0）的图象交于（x₁ ， y₁）和（x₂ ， y₂）两点，（）

A、若a<0，m<0，则x₁+x₂>2h B、若a>0，m<0，则x₁+x₂>2h C、若x₁+x₂>2h，则a>0，m>0 D、若x₁+x₂<2h，则a>0，m<0

查看试题解析
4. 方程 $7 x^{2} - (k + 13) x + k^{2} - k - 2 = 0$ （k是实数）有两个实根 $α$ 、 $β$ ，且 $0 < α < 1$ ， $1 < β < 2$ ，那么k的取值范围是（）

A、 $3 < k < 4$ B、 $- 2 < k < - 1$ C、 $3 < k < 4$ 或 $- 2 < k < - 1$ D、无解

查看试题解析
5. 如图，抛物线 $y = a x^{2} + b x + c$ 经过点 $(1 ， 0)$ 和 $(0 ， - 3)$ ，则下列结论：① $c = - 3$ ；② $a - b + c > 0$ ；③ $4 a c - b^{2} > 0$ ；④ $b < 3$ ；⑤若双曲线 $y = \frac{1}{x}$ 经过点 $(a c ， b)$ ，则以 $a$ 、 $b$ 为根的一元二次方程是 $x^{2} - 3 x - \frac{1}{3} = 0$ ．其中正确结论的个数为（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
6. 抛物线 $y = a x^{2} + b x + c$ （a，b，c为常数， $a < 0$ ）经过 $A (2 ， 0) ， B (- 4 ， 0)$ 两点，下列四个结论：
①一元二次方程 $a x^{2} + b x + c = 0$ 的根为 $x_{1} = 2 ， x_{2} = - 4$ ；②若点 $C (- 5 ， y_{1}) ， D (π ， y_{2})$ 在该抛物线上，则 $y_{1} < y_{2}$ ；③对于任意实数t，总有 $a t^{2} + b t \leq a - b$ ；④对于a的每一个确定值，若一元二次方程 $a x^{2} + b x + c = p$ （p为常数， $p > 0$ ）的根为整数，则p的值只有两个.其中正确的结论是（）

A、①② B、①②③ C、①③ D、①③④

查看试题解析
7. 规定：如果关于x的一元二次方程ax²+bx+c=0（a≠0）有两个实数根，且其中一个根是另一个根的2倍，则称这样的方程为“倍根方程”．现有下列结论：
①方程x²+2x﹣8=0是倍根方程；

②若关于x的方程x²+ax+2=0是倍根方程，则a=±3；

③若关于x的方程ax²﹣6ax+c=0（a≠0）是倍根方程，则抛物线y=ax²﹣6ax+c与x轴的公共点的坐标是（2，0）和（4，0）；

④若点（m，n）在反比例函数y= $\frac{4}{x}$ 的图象上，则关于x的方程mx²+5x+n=0是倍根方程．

上述结论中正确的有（）

A、①② B、③④ C、②③ D、②④

查看试题解析
8. 如图，二次函数y=ax²+bx+c（a≠0）的图象与x轴正半轴相交于A、B两点，与y轴相交于点C，对称轴为直线x=2，且OA=OC，则下列结论：
①abc＞0；②9a+3b+c＜0；③c＞﹣1；④关于x的方程ax²+bx+c=0（a≠0）有一个根为﹣ $\frac{1}{a}$
其中正确的结论个数有（）

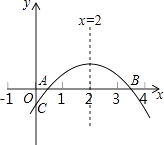A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 已知二次函数y＝ax²+bx+c（a≠0）的对称轴为直线x＝-1，与x轴的一个交点B的坐标为（1，0）其图象如图所示，下列结论：①abc＜0； ②2a-b＝0； ③一元二次方程ax²+bx+c＝0的两个根是-3和1；④当y＞0时，-3＜x＜1；⑤当x＞0时，y随x的增大而增大；⑥若点E（-4，y₁），F（-2，y₂），M（3，y₃）是函数图象上的三点，则y₁＞y₂＞y₃ ，其中正确的有（）个

A、5 B、4 C、3 D、2

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的部分图象如图所示，图象过点 $(- 1 ， 0)$ ，对称轴为直线 $x = 2$ ，下列结论：① $4 a + b = 0$ ；② $9 a + c > - 3 b$ ；③ $7 a - 3 b + 2 c > 0$ ；④若点 $A (- 3 ， y_{1}) ， B (- \frac{1}{2} ， y_{2}) ， C (\frac{7}{2} ， y_{3})$ 在该函数图象上，则 $y_{1} < y_{3} < y_{2}$ ；⑤若方程 $a (x + 1) (x - 5) = - 3$ 的两根为 $x_{1}$ 和 $x_{2}$ ，且 $x_{1} < x_{2}$ ，则 $x_{1} < - 1 < 5 < x_{2}$ ．其中正确的结论有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题（每题3分，共15分）

11. 二次函数y＝ax²+bx+c（a≠0）的图象经过（﹣1，0），（0，4），（t，4）三点，当t≥3时，一元二次方程ax²+bx+c＝n一定有实数根，则n的取值范围是．

查看试题解析
12. 若关于x的一元二次方程 $a x^{_{2}} - \frac{3}{2} x + \frac{1}{2} = 0$ 的两个不等实数根都在-1和1之间（不包括-1,1），则a的取值范围是.

查看试题解析
13. 已知，二次函数 $y = x^{2} - 2 x - 3$ ，规定 $y^{'} = | y |$ ，若使 $y^{'} = a$ 的正数x有且只有三个，则a的取值范围是.

查看试题解析
14. 已知抛物线 $y = a x^{2} + b x + c$ （a，b，c是常数）开口向下，过 $A (- 1 ， 0)$ ， $B (m ， 0)$ 且 $1 < m < 2$ ．下列四个结论：
① $b > 0$ ；②若 $m = \frac{3}{2}$ ，则 $3 a + 2 c < 0$ ；

③若点 $M (x_{1} ， y_{1})$ ， $N (x_{2} ， y_{2})$ 在抛物线上， $x_{1} < x_{2}$ ，且 $x_{1} + x_{2} > 1$ ，则 $y_{1} > y_{2}$ ；

④当 $a \leq - 1$ 时，关于x的一元二次方程 $a x^{2} + b x + c = 1$ 必有两个不相等的实数根．其中正确的是（填写序号）．

查看试题解析
15. 对于实数a，b，定义运算“*”： $a*b = a^{2} － ab (a \leq b)$ ； $a*b = b^{2} － ab (a > b)$ ，关于x的方程 $(2 x － 1) * (x － 1) = m$ 恰好有三个不相等的实数根，则m的取值范围是．

查看试题解析

三、解答题（共7题，共55分）

16. 数和形是数学研究客观物体的两个方面，数（代数）侧重研究物体数量方面，具有精确性、形（几何）侧重研究物体形的方面，具有直观性．数和形相互联系，可用数来反映空间形式，也可用形来说明数量关系．数形结合就是把两者结合起来考虑问题，充分利用代数、几何各自的优势，数形互化，共同解决问题．
同学们，请你结合所学的数学解决下列问题．

在平面直角坐标系中，若点的横坐标、纵坐标都为整数，则称这样的点为整点．设函数 $y = (4 a + 2) x^{2} + (9 - 6 a) x - 4 a + 4$ （实数 $a$ 为常数）的图象为图象 $T$ ．

(1)、求证：无论 $a$ 取什么实数，图象 $T$ 与 $x$ 轴总有公共点；

(2)、是否存在整数 $a$ ，使图象 $T$ 与 $x$ 轴的公共点中有整点？若存在，求所有整数 $a$ 的值；若不存在，请说明理由．

查看试题解析
17. 已知抛物线 $y = - x^{2} + b x + c$ 的顶点坐标为 $(\frac{\sqrt{7}}{2} ， \frac{11}{4})$ ，设 $k$ 是拋物线 $y = - x^{2} + b x + c$ 与 $x$ 轴交点的横坐标．

(1)、求抛物线的解析式．

(2)、求 $\frac{45 k^{2}}{k^{9} + k^{7} + 2 k^{5} + k^{3} + k}$ 的值．

查看试题解析
18. 我们把纵坐标是横坐标两倍的点叫双语点，如点 $A (2 ， 4)$ ，点 $B (- 3 ， - 6)$ .

(1)、函数 $y = 3 x + 1$ 的双语点是；

(2)、函数 $y = \frac{k}{x}$ （k为常数，目 $k \neq 0$ ）上是否存在双语点？若存在，求出双语点的坐标，若不存在，请说明理由；

(3)、函数 $y = \frac{1}{4} x^{2} + (n - k - 1) x + m + k + 2$ 的图象上只有唯一一个双语点，且当 $1 \leq n \leq 3$ 时，m的最小值为k，求实数k的值.

查看试题解析
19. 已知二次函数 $y = a x^{2} + b x + c (a > 0)$ ．

(1)、若 $a = 1 ， c = - 1$ ，且该二次函数的图象过点 $(2 ， 0)$ ，求 $b$ 的值；

(2)、如图所示，在平面直角坐标系 $O x y$ 中，该二次函数的图象与 $x$ 轴交于点 $A (x_{1} ， 0) ， B (x_{2} ， 0)$ ，且 $x_{1} < 0 < x_{2}$ ，点D在 $⊙ O$ 上且在第二象限内，点 $E$ 在 $x$ 轴正半轴上，连接 $D E$ ，且线段 $D E$ 交 $y$ 轴正半轴于点 $F$ ， $∠ D O F = ∠ D E O ， O F = \frac{3}{2} D F$ ．

①求证： $\frac{D O}{E O} = \frac{2}{3}$ ．
②当点 $E$ 在线段 $O B$ 上，且 $B E = 1$ ． $⊙ O$ 的半径长为线段 $O A$ 的长度的 $2$ 倍，若 $4 a c = - a^{2} - b^{2}$ ，求 $2 a + b$ 的值．

查看试题解析
20. 已知关于x的一元二次方程ax²+x+2=0.

(1)、求证：当a＜0时，方程ax²+x+2=0一定有两个不等的实数根；

(2)、若代数式﹣x²+x+2的值为正整数，且x为整数时，求x的值；

(3)、当a=a₁时，抛物线y=ax²+x+2与x轴的正半轴相交于点M（m，0）；当a=a₂时，抛物线y=ax²+x+2与x轴的正半轴相交于点N（n，0）；若点M在点N的左边，试比较a₁与a₂的大小.

查看试题解析
21. 借鉴已有研究函数的经验，探索函数 $y = | x^{2} - 2 x - 3 | - 2$ 的图象与性质，研究过程如下，请补充完整.

(1)、自变量x的取值范围是全体实数，x与y的几组对应值列表如下：

其中： $m =$ ， $n =$ .

(2)、根据列表数据，在如图所示的平面直角坐标系中描点，并画出函数图象；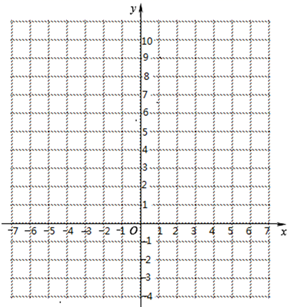

(3)、观察函数图象：
①写出函数的一条性质

②当方程 $| x^{2} - 2 x - 3 | = b + 2$ 有且仅有两个不相等的实数根，根据函数图象直接写出b的取值范围..

查看试题解析
22. 我们约定[a， $-$ b，c]为二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的“相关数”．
【特例感知】
“相关数”为[1，4，3]的二次函数的解析式为 $y_{1} = x^{2} - 4 x + 3$ ，
“相关数”为[2，5，3]的二次函数的解析式为 $y_{2} = 2 x^{2} - 5 x + 3$ ；
“相关数”为[3，6，3]的二次函数的解析式为 $y_{3} = 3 x^{2} - 6 x + 3$ ；

(1)、下列结论正确的是（填序号）．
①抛物线 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 都经过点 $(0 ， 3)$ ；
②抛物线 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 与直线 $y = 3$ 都有两个交点；
③抛物线 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 有两个交点．

(2)、【形成概念】
把满足“相关数”为[n，n+3，3]（n为正整数）的抛物线 $y_{n}$ 称为“一簇抛物线”，分别记为 $y_{1}$ ， $y_{2}$ ， $y_{3}$ ， …， $y_{n}$ ．抛物线 $y_{n}$ 与x轴的交点为 $A_{n}$ ， $B_{n}$ ．
【探究问题】
①“—簇抛物线” $y_{1}$ ， $y_{2}$ ， $y_{3}$ ， …， $y_{n}$ 都经过两个定点，这两个定点的坐标分别为．
②拋物线 $y_{n}$ 的顶点为 $C_{n}$ ，是否存在正整数n，使 $△$ $A_{n} B_{n} C_{n}$ 是直角三角形？若存在，请求出n的值；若不存在，请说明理由．
③当 $n \geq 4$ 时，抛物线 $y_{n}$ 与x轴的左交点 $A_{n}$ ，与直线 $y = 3$ 的一个交点为 $D_{n}$ ，且点 $D_{n}$ 不在y轴上．判断 $A_{n} A_{n + 1}$ 和 $D_{n} D_{n + 1}$ 是否相等，并说明理由．

查看试题解析