【培优卷】2.4二次函数的应用—北师大版数学九年级下册同步测试
试卷更新日期:2023-09-17 类型:同步测试
一、选择题(每题2分,共20分)
-
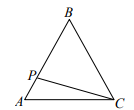
1. 如图,正三角形ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止.设运动时间为x(秒),y=PC2 , 则y关于x的函数的图象大致是( )
 A、
A、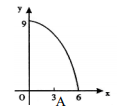 B、
B、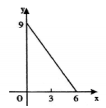 C、
C、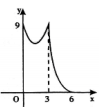 D、
D、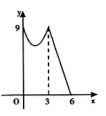 2. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
2. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( ) A、
A、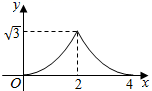 B、
B、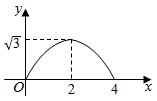 C、
C、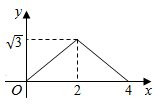 D、
D、 3. 学校组织学生去绍兴进行研学实践活动,小王同学发现在宾馆房间的洗手盘台面上有一瓶洗手液(如图①).于是好奇的小王同学进行了实地测量研究.当小王用一定的力按住顶部A下压如图②位置时,洗手液从喷口B流出,路线近似呈抛物线状,且喷口B为该抛物线的顶点.洗手液瓶子的截面图下面部分是矩形.小王同学测得∶洗手液瓶子的底面直径 , 喷嘴位置点B距台面的距离为 , 且三点共线.小王在距离台面处接洗手液时,手心Q到直线的水平距离为 , 若小王不去接,则洗手液落在台面的位置距的水平面是( )
3. 学校组织学生去绍兴进行研学实践活动,小王同学发现在宾馆房间的洗手盘台面上有一瓶洗手液(如图①).于是好奇的小王同学进行了实地测量研究.当小王用一定的力按住顶部A下压如图②位置时,洗手液从喷口B流出,路线近似呈抛物线状,且喷口B为该抛物线的顶点.洗手液瓶子的截面图下面部分是矩形.小王同学测得∶洗手液瓶子的底面直径 , 喷嘴位置点B距台面的距离为 , 且三点共线.小王在距离台面处接洗手液时,手心Q到直线的水平距离为 , 若小王不去接,则洗手液落在台面的位置距的水平面是( )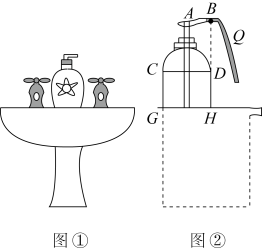 A、 B、 C、 D、4. 小明发现鸡蛋的形状可以近似用抛物线与圆来刻画.于是他画了两只鸡蛋的示意图(如图,单位:cm),其中 AB 和 A'B';上方为两条开口大小相同的抛物线,下方为两个圆的一部分.若第一个鸡蛋的高度 CD 为 8.4 cm,则第二个鸡蛋的高度C'D'为( )
A、 B、 C、 D、4. 小明发现鸡蛋的形状可以近似用抛物线与圆来刻画.于是他画了两只鸡蛋的示意图(如图,单位:cm),其中 AB 和 A'B';上方为两条开口大小相同的抛物线,下方为两个圆的一部分.若第一个鸡蛋的高度 CD 为 8.4 cm,则第二个鸡蛋的高度C'D'为( )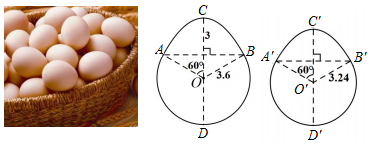 A、7.29 cm B、7.34 cm C、7.39 cm D、7.44 cm5. 我校门口道路的隔离栏通常会涂上醒目的颜色,呈抛物线形状(如图1),图2是一个长为2米,宽为1米的矩形隔离栏,中间被4根栏杆五等分,每根栏杆的下面一部分涂上醒目的蓝色,颜色的分界处(点E , 点P)以及点A , 点B落上同一条抛物线上,若第1根栏杆涂色部分(EF)与第2根栏杆未涂色部分(PQ)长度相等,则EF的长度是( )
A、7.29 cm B、7.34 cm C、7.39 cm D、7.44 cm5. 我校门口道路的隔离栏通常会涂上醒目的颜色,呈抛物线形状(如图1),图2是一个长为2米,宽为1米的矩形隔离栏,中间被4根栏杆五等分,每根栏杆的下面一部分涂上醒目的蓝色,颜色的分界处(点E , 点P)以及点A , 点B落上同一条抛物线上,若第1根栏杆涂色部分(EF)与第2根栏杆未涂色部分(PQ)长度相等,则EF的长度是( )
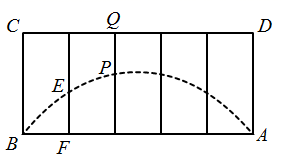 A、 米 B、 米 C、 米 D、 米6. 洗手盘台面上有一瓶洗手液.当同学用一定的力按住顶部下压如图位置时,洗手液从喷口流出,路线近似呈抛物线状,且喷口为该抛物线的顶点.洗手液瓶子的截面图下面部分是矩形同学测得:洗手液瓶子的底面直径 , 喷嘴位置点距台面的距离为 , 且、、三点共线.在距离台面处接洗手液时,手心到直线的水平距离为 , 不去接则洗手液落在台面的位置距的水平面是 . ( )
A、 米 B、 米 C、 米 D、 米6. 洗手盘台面上有一瓶洗手液.当同学用一定的力按住顶部下压如图位置时,洗手液从喷口流出,路线近似呈抛物线状,且喷口为该抛物线的顶点.洗手液瓶子的截面图下面部分是矩形同学测得:洗手液瓶子的底面直径 , 喷嘴位置点距台面的距离为 , 且、、三点共线.在距离台面处接洗手液时,手心到直线的水平距离为 , 不去接则洗手液落在台面的位置距的水平面是 . ( )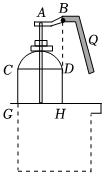 A、 B、 C、 D、7. 一位运动员在离篮筐水平距离4m处起跳投篮,球运行路线可看作抛物线,当球离开运动员的水平距离为1m时,它与篮筐同高,球运行中的最大高度为3.5m,最后准确落入篮筐,已知篮筐到地面的距离为3.05m,该运动员投篮出手点距离地面的高度为( )
A、 B、 C、 D、7. 一位运动员在离篮筐水平距离4m处起跳投篮,球运行路线可看作抛物线,当球离开运动员的水平距离为1m时,它与篮筐同高,球运行中的最大高度为3.5m,最后准确落入篮筐,已知篮筐到地面的距离为3.05m,该运动员投篮出手点距离地面的高度为( ) A、1.5m B、2m C、2.25m D、2.5m8. 一种包装盒的设计方法如图所示,四边形ABCD是边长为30cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四点重合于图中的点O,形成一个底面为正方形的长方体包装盒.设BE=CF=xcm,要使包装盒的侧面积最大,则x应取( )
A、1.5m B、2m C、2.25m D、2.5m8. 一种包装盒的设计方法如图所示,四边形ABCD是边长为30cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四点重合于图中的点O,形成一个底面为正方形的长方体包装盒.设BE=CF=xcm,要使包装盒的侧面积最大,则x应取( )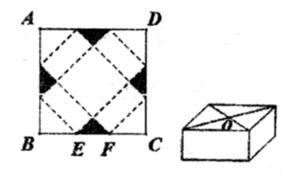 A、12.5cm B、10cm C、7.5cm D、5cm9. 物理课上我们学习了竖直上抛运动,若从地面竖直向上抛一小球,小球的高度单位:与小球运动时间单位:之间的函数关系如图所示,下列结论:
A、12.5cm B、10cm C、7.5cm D、5cm9. 物理课上我们学习了竖直上抛运动,若从地面竖直向上抛一小球,小球的高度单位:与小球运动时间单位:之间的函数关系如图所示,下列结论:①小球在空中经过的路程是
②小球抛出后,速度越来越快
③小球抛出时速度为0
④小球的高度时,
其中正确的是( )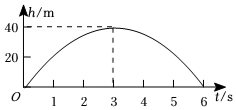 A、①②③ B、①② C、②③④ D、②③10. 某公司销售一种藜麦,成本价为30元/千克,若以35元/千克的价格销售,每天可售出450千克.当售价每涨0.5元/千克时,日销售量就会减少15千克.设当日销售单价为 (元/千克)( ,且 是按0.5的倍数上涨),当日销售量为 (千克).有下列说法:
A、①②③ B、①② C、②③④ D、②③10. 某公司销售一种藜麦,成本价为30元/千克,若以35元/千克的价格销售,每天可售出450千克.当售价每涨0.5元/千克时,日销售量就会减少15千克.设当日销售单价为 (元/千克)( ,且 是按0.5的倍数上涨),当日销售量为 (千克).有下列说法:①当 时, ② 与 之间的函数关系式为 ③若使日销售利润为2880元,且销售量较大,则日销售单价应定为42元/千克④若使日销售利润最大,销售价格应定为40元/千克
其中正确的是( )
A、①② B、①②④ C、①②③ D、②④二、填空题(每题3分,共15分)
-
11. 年5月8日,商业首航完成——中国民商业运营国产大飞机正式起步.时分航班抵达北京首都机场,穿过隆重的“水门礼”(寓意“接风洗尘”、是国际民航中高级别的礼仪).如图①,在一次“水门礼”的预演中,两辆消防车面向飞机喷射水柱,喷射的两条水柱近似看作形状相同的抛物线的一部分.如图②,当两辆消防车喷水口A、B的水平距离为米时,两条水柱在物线的顶点H处相遇,此时相遇点H距地面米,喷水口A、B距地面均为4米.若两辆消防车同时后退米,两条水柱的形状及喷水口、到地面的距离均保持不变,则此时两条水柱相遇点距地面米.
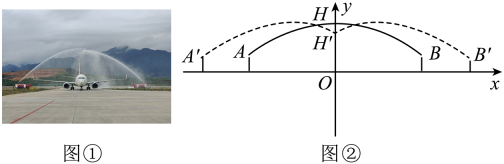 12. 某学生推铅球,铅球所经过的路线是抛物线的一部分,若这名学生出手点A(0,1.6),铅球路线最高处为B(6,4),则该学生将铅球推出的距离是 .13. 如图是一个横断面为抛物线形状的拱桥,当拱顶(拱桥洞的最高点)离水面时,水面宽 , 当水面下降时,水面的宽度为m.
12. 某学生推铅球,铅球所经过的路线是抛物线的一部分,若这名学生出手点A(0,1.6),铅球路线最高处为B(6,4),则该学生将铅球推出的距离是 .13. 如图是一个横断面为抛物线形状的拱桥,当拱顶(拱桥洞的最高点)离水面时,水面宽 , 当水面下降时,水面的宽度为m.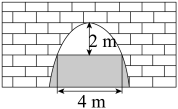 14. 如图所示,从高为2m的点 处向右上抛一个小球 ,小球路线呈抛物线 形状,小球水平经过2m时达到最大高度6m,然后落在下方台阶B处弹起,已知 m, m, m,若小球弹起形成一条与 形状相同的抛物线,且落点 与 , 在同一直线上,则小球弹起时的最大高度是m
14. 如图所示,从高为2m的点 处向右上抛一个小球 ,小球路线呈抛物线 形状,小球水平经过2m时达到最大高度6m,然后落在下方台阶B处弹起,已知 m, m, m,若小球弹起形成一条与 形状相同的抛物线,且落点 与 , 在同一直线上,则小球弹起时的最大高度是m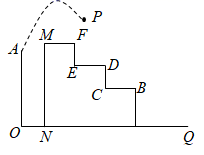 15. 图1是一个高脚杯截面图, 杯体CBD呈抛物线状(杯体厚度不计) ,点B是抛物线的顶点,AB=9,EF=2 ,点A是EF的中点,当高脚杯中装满液体时,液面CD=4 ,此时最大深度(液面到最低点的距离)为12,将高脚杯绕点F缓缓倾斜倒出部分液体,当∠EFH=30°时停止,此时液面为GD,则液面GD到平面l的距离是;此时杯体内液体的最大深度为。
15. 图1是一个高脚杯截面图, 杯体CBD呈抛物线状(杯体厚度不计) ,点B是抛物线的顶点,AB=9,EF=2 ,点A是EF的中点,当高脚杯中装满液体时,液面CD=4 ,此时最大深度(液面到最低点的距离)为12,将高脚杯绕点F缓缓倾斜倒出部分液体,当∠EFH=30°时停止,此时液面为GD,则液面GD到平面l的距离是;此时杯体内液体的最大深度为。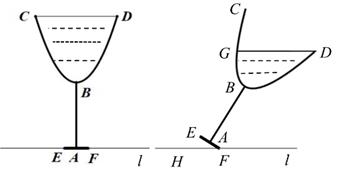
三、解答题(共7题,共65分)
-
16. 某商店为了推销一种新产品,在某地先后举行40场产品发布会,已知该产品每台成本为10万元,设第x场产品的销售量为y(台),已知第一场销售产品49台,然后每增加一场,产品就少卖出1台;(1)、直接写出y与x之间满足的函数关系式;产品的每场销售单价p(万元)由基本价和浮动价两部分相加组成,其中基本价保持不变,经过统计,发现第1场—第20场浮动价与发布场次x成正比,第21场—第40场浮动价与发布场次x成反比,得到如下数据:
x(场)
3
10
25
p(万元)
10.6
12
14.2
(2)、求p与x之间满足的函数关系式;(3)、当产品销售单价为13万元时,求销售场次是第几场?(4)、在这40场产品发布会中,求哪一场获得的利润最大,最大利润是多少?17. 某工厂用 天时间生产一款新型节能产品,每天生产的该产品被某网店以每件 元的价格全部订购,在生产过程中,由于技术的不断更新,该产品第 天的生产成本 (元/件)与 (天)之间的关系如图所示,第 天该产品的生产量 (件)与 (天)满足关系式(1)、第 天,该厂生产该产品的利润是元;(2)、设第x天该厂生产该产品的利润为w元.①求w与x之间的函数关系式,并指出第几天的利润最大,最大利润是多少?
②在生产该产品的过程中,当天利润不低于 元的共有多少天?
 18. 为了有效地应对高楼火灾,某消防中队进行消防技能比赛.如图,在一个废弃高楼距地面的点A和的点B处,各设置了一个火源,消防员来到火源正前方,水枪喷出的水流看作抛物线的一部分(水流出口与地面的距离忽略不计).第一次灭火时站在水平地面的点C处,水流恰好到达点A处,且水流的最大高度为 , 水流的最高点到高楼的水平距离为 , 建立如图所示的平面直角坐标系,水流的高度y(m)与到高楼的水平距离x(m)之间的函数关系式为: .
18. 为了有效地应对高楼火灾,某消防中队进行消防技能比赛.如图,在一个废弃高楼距地面的点A和的点B处,各设置了一个火源,消防员来到火源正前方,水枪喷出的水流看作抛物线的一部分(水流出口与地面的距离忽略不计).第一次灭火时站在水平地面的点C处,水流恰好到达点A处,且水流的最大高度为 , 水流的最高点到高楼的水平距离为 , 建立如图所示的平面直角坐标系,水流的高度y(m)与到高楼的水平距离x(m)之间的函数关系式为: .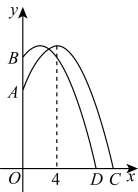 (1)、求消防员第一次灭火时水流所在抛物线的解析式;(2)、待A处火熄灭后,消防员前进2m到点D处进行第二次灭火,若两次灭火时水流所在抛物线的形状相同,请判断水流是否到达点B处,并说明理由;(3)、若消防员站在到高楼的水平距离为11m~12m的地方,调整水枪,使喷出的水流形状发生变化,水流的最高点到高楼的水平距高始终是4m,当时,求水流到达墙面高度的取值范围.19. 如图1,隧道截面由抛物线的一部分AED和矩形ABCD构成,矩形的一边BC为12米,另一边AB为2米.以BC所在的直线为x轴,线段BC的垂直平分线为y轴,建立平面直角坐标系xOy,规定一个单位长度代表1米.E(0,8)是抛物线的顶点.
(1)、求消防员第一次灭火时水流所在抛物线的解析式;(2)、待A处火熄灭后,消防员前进2m到点D处进行第二次灭火,若两次灭火时水流所在抛物线的形状相同,请判断水流是否到达点B处,并说明理由;(3)、若消防员站在到高楼的水平距离为11m~12m的地方,调整水枪,使喷出的水流形状发生变化,水流的最高点到高楼的水平距高始终是4m,当时,求水流到达墙面高度的取值范围.19. 如图1,隧道截面由抛物线的一部分AED和矩形ABCD构成,矩形的一边BC为12米,另一边AB为2米.以BC所在的直线为x轴,线段BC的垂直平分线为y轴,建立平面直角坐标系xOy,规定一个单位长度代表1米.E(0,8)是抛物线的顶点.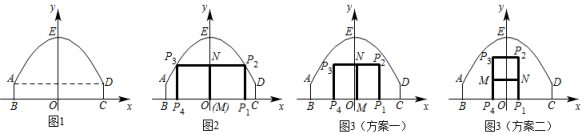 (1)、求此抛物线对应的函数表达式;(2)、在隧道截面内(含边界)修建“
(1)、求此抛物线对应的函数表达式;(2)、在隧道截面内(含边界)修建“ ”型或“
”型或“ ”型栅栏,如图2、图3中粗线段所示,点 , 在x轴上,MN与矩形的一边平行且相等.栅栏总长l为图中粗线段 , , , MN长度之和.请解决以下问题:
”型栅栏,如图2、图3中粗线段所示,点 , 在x轴上,MN与矩形的一边平行且相等.栅栏总长l为图中粗线段 , , , MN长度之和.请解决以下问题:(ⅰ)修建一个“
 ”型栅栏,如图2,点 , 在抛物线AED上.设点的横坐标为 , 求栅栏总长l与m之间的函数表达式和l的最大值;
”型栅栏,如图2,点 , 在抛物线AED上.设点的横坐标为 , 求栅栏总长l与m之间的函数表达式和l的最大值;(ⅱ)现修建一个总长为18的栅栏,有如图3所示的修建“
 ”型或“
”型或“ ”型栅型两种设计方案,请你从中选择一种,求出该方案下矩形面积的最大值,及取最大值时点的横坐标的取值范围(在右侧).20. 如图1的小山丘是科研部门的小球弹射实验场地,在小山丘一侧的山坡上建有小球弹射发射装置,另一侧建有圆柱形小球接收装置,如图2为实验场地的纵截面示意图,小山丘纵截面的外部轮廓线近似为抛物线的一部分,以小山丘纵截面与地面的交线为x轴,以过发射装置所在的直线AB为y轴,建立平面直角坐标系,发射装置底部在轮廓线的点A处,距离地面为1米,在发射装置3米的点B处是发射点,已知小山丘纵截面的外部轮廓线为 , 从发射装置的发射点弹射一个小球(忽略空气阻力)时,小球的飞行路线为一段抛物线 .
”型栅型两种设计方案,请你从中选择一种,求出该方案下矩形面积的最大值,及取最大值时点的横坐标的取值范围(在右侧).20. 如图1的小山丘是科研部门的小球弹射实验场地,在小山丘一侧的山坡上建有小球弹射发射装置,另一侧建有圆柱形小球接收装置,如图2为实验场地的纵截面示意图,小山丘纵截面的外部轮廓线近似为抛物线的一部分,以小山丘纵截面与地面的交线为x轴,以过发射装置所在的直线AB为y轴,建立平面直角坐标系,发射装置底部在轮廓线的点A处,距离地面为1米,在发射装置3米的点B处是发射点,已知小山丘纵截面的外部轮廓线为 , 从发射装置的发射点弹射一个小球(忽略空气阻力)时,小球的飞行路线为一段抛物线 .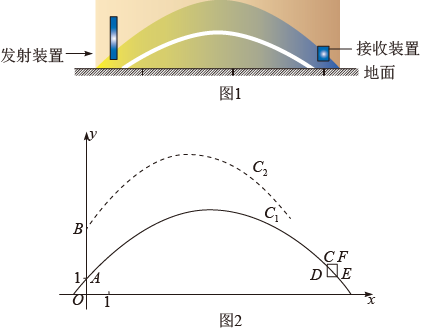 (1)、直接写出c的值,当小球离B处的水平距离和竖直距离都为4米时,求b的值,并求小球到小山丘的竖直距离为1米时,小球离B处的水平距离;(2)、若小球最远着陆点到y轴的距离为15米,当小球飞行到小山丘顶的正上方,且与顶部距离不小于米时,求b的取值范围,并求小球飞行路线的顶点到x轴距离的最小值;(3)、圆柱形小球接收装置的最大截面为矩形CDEF,已知点E在上,其横坐标为14,轴, , . 若小球恰好落入该装置内(不触碰装置侧壁),请直接写出b的取值范围.21. 如图1,小明将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得AB=5,AD=4.在进行如下操作时遇到了下列几个问题,请你帮助解决.
(1)、直接写出c的值,当小球离B处的水平距离和竖直距离都为4米时,求b的值,并求小球到小山丘的竖直距离为1米时,小球离B处的水平距离;(2)、若小球最远着陆点到y轴的距离为15米,当小球飞行到小山丘顶的正上方,且与顶部距离不小于米时,求b的取值范围,并求小球飞行路线的顶点到x轴距离的最小值;(3)、圆柱形小球接收装置的最大截面为矩形CDEF,已知点E在上,其横坐标为14,轴, , . 若小球恰好落入该装置内(不触碰装置侧壁),请直接写出b的取值范围.21. 如图1,小明将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得AB=5,AD=4.在进行如下操作时遇到了下列几个问题,请你帮助解决.
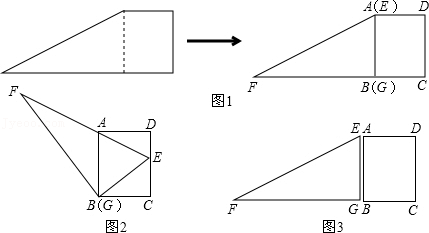 (1)、如图2,将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时EF恰好经过点A , 请证明:△ADE∽△FGE;(2)、如图3,在(1)的条件下,小明先将△EFG的边EG和矩形的边AB重合,然后将△EFG沿直线BC向右平移,至F点与B重合时停止.在平移过程中,设G点平移的距离为x , 两纸片重叠部分面积为y , 求在平移的整个过程中,y与x的函数关系式.(3)、如图,在(1)的条件下,小明把该图形放在直角坐标系中,使B(G)为坐标原点BC为x轴,在x轴和y上分别找P,Q两点使△DPQ与△ABF相似,直接写出P点的坐标。22.
(1)、如图2,将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时EF恰好经过点A , 请证明:△ADE∽△FGE;(2)、如图3,在(1)的条件下,小明先将△EFG的边EG和矩形的边AB重合,然后将△EFG沿直线BC向右平移,至F点与B重合时停止.在平移过程中,设G点平移的距离为x , 两纸片重叠部分面积为y , 求在平移的整个过程中,y与x的函数关系式.(3)、如图,在(1)的条件下,小明把该图形放在直角坐标系中,使B(G)为坐标原点BC为x轴,在x轴和y上分别找P,Q两点使△DPQ与△ABF相似,直接写出P点的坐标。22. (1)、【探索发现】 如图1,是一张直角三角形纸片, ,小明想从中剪出一个以 为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为.(2)、【拓展应用】如图2,在 中, ,BC边上的高 ,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,求出矩形PQMN面积的最大值 用含a、h的代数式表示 ;(3)、【灵活应用】如图3,有一块“缺角矩形”ABCDE, , , , ,小明从中剪出了一个面积最大的矩形 为所剪出矩形的内角 ,直接写出该矩形的面积.
(1)、【探索发现】 如图1,是一张直角三角形纸片, ,小明想从中剪出一个以 为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为.(2)、【拓展应用】如图2,在 中, ,BC边上的高 ,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,求出矩形PQMN面积的最大值 用含a、h的代数式表示 ;(3)、【灵活应用】如图3,有一块“缺角矩形”ABCDE, , , , ,小明从中剪出了一个面积最大的矩形 为所剪出矩形的内角 ,直接写出该矩形的面积.