【培优卷】2.2二次函数的图象与性质—北师大版数学九年级下册同步测试
试卷更新日期:2023-09-17 类型:同步测试
一、选择题(每题2分,共20分)
-
1. 如图,在平面直角坐标系中,直线与抛物线相交于点 , . 结合图象,判断下列结论:①当时,;②是方程的一个解;③若 , 是抛物线上的两点,则;④对于抛物线, , 当时,的取值范围是 . 其中正确结论的个数是( )
 A、4个 B、3个 C、2个 D、1个2. 二次函数的图象如图所示,对称轴是直线 , 下列结论:①;②方程()必有一个根大于2且小于3;③若是抛物线上的两点,那么;④;⑤对于任意实数m,都有 , 其中正确结论的个数是( )
A、4个 B、3个 C、2个 D、1个2. 二次函数的图象如图所示,对称轴是直线 , 下列结论:①;②方程()必有一个根大于2且小于3;③若是抛物线上的两点,那么;④;⑤对于任意实数m,都有 , 其中正确结论的个数是( ) A、5 B、4 C、3 D、23. 抛物线(a,b,c为常数,)经过 , 两点.则下列四个结论正确的有( )
A、5 B、4 C、3 D、23. 抛物线(a,b,c为常数,)经过 , 两点.则下列四个结论正确的有( )①;②;③若该抛物线与直线有交点,则a的取值范围是;④对于a的每一个确定值,如果一元二次方程(t为常数,)的根为整数,则t的值只有3个.
A、1个 B、2个 C、3个 D、4个4. 已知反比例函数在第一象限内的图象与一次函数的图象如图所示,则函数的图象可能为( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 规定:在平面直角坐标系中,横坐标与纵坐标均为整数的点为整点.对于题目:抛物线与轴分别交于、两点(点M在点N的左侧), , 线段与抛物线围成的封闭区域记作(包括边界),若区域内有6个整点,求的取值范围.则( )A、 B、 C、或 D、或6. 已知二次函数的图象如图所示,下列四个命题:①;②;③若 , 是该抛物线上的两点,则;④若 , 是该抛物线上的两点,则;其中正确的结论有( )
5. 规定:在平面直角坐标系中,横坐标与纵坐标均为整数的点为整点.对于题目:抛物线与轴分别交于、两点(点M在点N的左侧), , 线段与抛物线围成的封闭区域记作(包括边界),若区域内有6个整点,求的取值范围.则( )A、 B、 C、或 D、或6. 已知二次函数的图象如图所示,下列四个命题:①;②;③若 , 是该抛物线上的两点,则;④若 , 是该抛物线上的两点,则;其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个7. 规定二次函数的相关函数是.已知点 , 的坐标分别为 , , 连接 , 若线段与二次函数的相关函数的图象有两个公共点,则n的取值范围为( )A、或 B、或 C、或 D、或8. 在下列函数图象上任取不同的两点P(x1 , y1), Q(x2 , y2), 一定能使的是( )A、y=(x>0) B、y=-(x-2)2+5(x≥0) C、y=(x-3)2-4(x<0) D、y=3x+79. 如图,抛物线y=x2-2x+c与x轴交于点A,B两点,与y轴负半轴交于点C,其顶点为M,点D,E分别是AB,BM的中点,若△DEB与△ACD的面积比为9:10,则c的值为( )
A、1个 B、2个 C、3个 D、4个7. 规定二次函数的相关函数是.已知点 , 的坐标分别为 , , 连接 , 若线段与二次函数的相关函数的图象有两个公共点,则n的取值范围为( )A、或 B、或 C、或 D、或8. 在下列函数图象上任取不同的两点P(x1 , y1), Q(x2 , y2), 一定能使的是( )A、y=(x>0) B、y=-(x-2)2+5(x≥0) C、y=(x-3)2-4(x<0) D、y=3x+79. 如图,抛物线y=x2-2x+c与x轴交于点A,B两点,与y轴负半轴交于点C,其顶点为M,点D,E分别是AB,BM的中点,若△DEB与△ACD的面积比为9:10,则c的值为( ) A、 B、-2 C、 D、-310. 已知函数y=﹣x2+2ax,当x≤2时,函数值随x增大而增大,且对任意的1≤x1≤a+1和1≤x2≤a+1,x1、x2相应的函数值y1、y2总满足|y1﹣y2|≤16,则实数a的取值范围是( )A、2≤a≤5 B、﹣3≤a≤5 C、a≥2 D、2≤a≤3
A、 B、-2 C、 D、-310. 已知函数y=﹣x2+2ax,当x≤2时,函数值随x增大而增大,且对任意的1≤x1≤a+1和1≤x2≤a+1,x1、x2相应的函数值y1、y2总满足|y1﹣y2|≤16,则实数a的取值范围是( )A、2≤a≤5 B、﹣3≤a≤5 C、a≥2 D、2≤a≤3二、填空题(每题3分,共15分)
-
11. 定义:若一个函数图象上存在横纵坐标相等的点,则称该点为这个函数图象的“等值点”.例如,点是函数的图象的“等值点”.若函数的图象记为 , 将其沿直线翻折后的图象记为 . 当、两部分组成的图象上恰有2个“等值点”时,的取值范围为 .12. 如图,点A是抛物线对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,则三角形OAO′的面积为 .
 13. 已知二次函数y1=2x2-8x+3的图象与y轴交于点A,过点A的直线y2=kx+b与二次函数的图象交于另一点B(B在A的右侧),点P(m,n)在直线下方的二次函数图象上(包括端点A,B),若n的最大值与最小值的和为1,则点B的横坐标为 .14. 抛物线的图象如图所示,点A1 , A2 , A3 , A4…,A2022在抛物线第一象限的图象上,点B1 , B2 , B3 , B4. . .,B2022在y轴的正半轴上,、、…、都是等腰直角三角形,则 .
13. 已知二次函数y1=2x2-8x+3的图象与y轴交于点A,过点A的直线y2=kx+b与二次函数的图象交于另一点B(B在A的右侧),点P(m,n)在直线下方的二次函数图象上(包括端点A,B),若n的最大值与最小值的和为1,则点B的横坐标为 .14. 抛物线的图象如图所示,点A1 , A2 , A3 , A4…,A2022在抛物线第一象限的图象上,点B1 , B2 , B3 , B4. . .,B2022在y轴的正半轴上,、、…、都是等腰直角三角形,则 . 15. 如图,“心”形是由抛物线 和它绕着原点O , 顺时针旋转60°的图形经过取舍而成的,其中顶点C的对应点为D , 点A , B是两条抛物线的两个交点,点E , F , G是抛物线与坐标轴的交点,则AB= .
15. 如图,“心”形是由抛物线 和它绕着原点O , 顺时针旋转60°的图形经过取舍而成的,其中顶点C的对应点为D , 点A , B是两条抛物线的两个交点,点E , F , G是抛物线与坐标轴的交点,则AB= .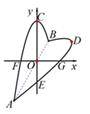
三、解答题(共7题,共65分)
-
16. 如图,在平而直角坐标系中,二次函数的图象与轴分别交于点 , 顶点为 . 连接 , 将线段绕点按顺时针方向旋转得到线段 , 连接 . 点分别在线段上,连接与交于点 .
 (1)、求点的坐标;(2)、随着点线段上运动.
(1)、求点的坐标;(2)、随着点线段上运动.①的大小是否发生变化?请说明理由;
②线段的长度是否存在最大值?若存在,求出最大值;若不存在,请说明理由;
(3)、当线段的中点在该二次函数的因象的对称轴上时,的面积为.17. 如图,二次函数的图象与轴的正半轴交于点A,经过点A的直线与该函数图象交于点 , 与轴交于点C.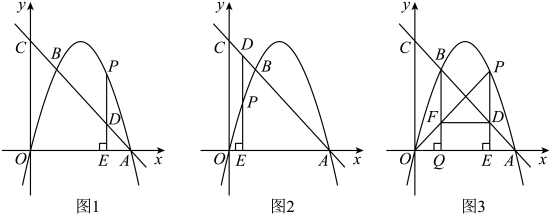 (1)、求直线的函数表达式及点C的坐标;(2)、点是第一象限内二次函数图象上的一个动点,过点作直线轴于点 , 与直线交于点D,设点的横坐标为 .
(1)、求直线的函数表达式及点C的坐标;(2)、点是第一象限内二次函数图象上的一个动点,过点作直线轴于点 , 与直线交于点D,设点的横坐标为 .①当时,求的值;
②当点在直线上方时,连接 , 过点作轴于点 , 与交于点 , 连接 . 设四边形的面积为 , 求关于的函数表达式,并求出S的最大值.
18. 如图,抛物线与y轴交于点 , 顶点坐标为 , C是x轴上一动点. (1)、求b,c的值.(2)、当周长最小时,求点C的坐标.(3)、设m是抛物线与x轴的交点的横坐标,求的值.19. 抛物线交x轴于A,B两点(A在B的左边),C是第一象限抛物线上一点,直线交y轴于点P.
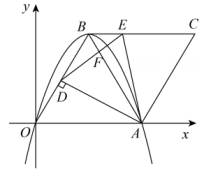
(1)、求b,c的值.(2)、当周长最小时,求点C的坐标.(3)、设m是抛物线与x轴的交点的横坐标,求的值.19. 抛物线交x轴于A,B两点(A在B的左边),C是第一象限抛物线上一点,直线交y轴于点P. (1)、直接写出A,B两点的坐标;(2)、如图①,当时,在抛物线上存在点D(异于点B),使B,D两点到的距离相等,求出所有满足条件的点D的横坐标;(3)、如图②,直线交抛物线于另一点E,连接交y轴于点F,点C的横坐标为m,求的值(用含m的式子表示).20. 如图,抛物线与轴交于点 , 点 , 与轴交于点 , 点与点关于轴对称,点是抛物线上的一个动点.
(1)、直接写出A,B两点的坐标;(2)、如图①,当时,在抛物线上存在点D(异于点B),使B,D两点到的距离相等,求出所有满足条件的点D的横坐标;(3)、如图②,直线交抛物线于另一点E,连接交y轴于点F,点C的横坐标为m,求的值(用含m的式子表示).20. 如图,抛物线与轴交于点 , 点 , 与轴交于点 , 点与点关于轴对称,点是抛物线上的一个动点.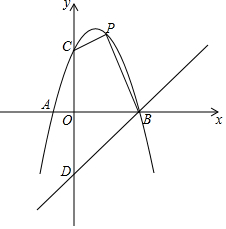 (1)、求直线的解析式;(2)、当点在第一象限时,求四边形面积的最大值,并求出此时点的坐标;(3)、在点的运动过程中,是否存在点 , 使是以为直角边的直角三角形?若存在,求出点的坐标;若不存在,请说明理由.21. 如图,二次函数的图象与x轴相交于点 , 其顶点是C .
(1)、求直线的解析式;(2)、当点在第一象限时,求四边形面积的最大值,并求出此时点的坐标;(3)、在点的运动过程中,是否存在点 , 使是以为直角边的直角三角形?若存在,求出点的坐标;若不存在,请说明理由.21. 如图,二次函数的图象与x轴相交于点 , 其顶点是C .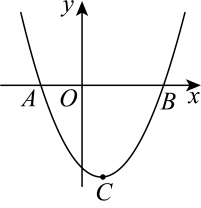
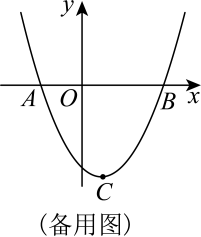 (1)、;(2)、D是第三象限抛物线上的一点,连接OD , ;将原抛物线向左平移,使得平移后的抛物线经过点D , 过点作x轴的垂线l . 已知在l的左侧,平移前后的两条抛物线都下降,求k的取值范围;(3)、将原抛物线平移,平移后的抛物线与原抛物线的对称轴相交于点Q , 且其顶点P落在原抛物线上,连接PC、QC、PQ . 已知是直角三角形,求点P的坐标.22. 如图
(1)、;(2)、D是第三象限抛物线上的一点,连接OD , ;将原抛物线向左平移,使得平移后的抛物线经过点D , 过点作x轴的垂线l . 已知在l的左侧,平移前后的两条抛物线都下降,求k的取值范围;(3)、将原抛物线平移,平移后的抛物线与原抛物线的对称轴相交于点Q , 且其顶点P落在原抛物线上,连接PC、QC、PQ . 已知是直角三角形,求点P的坐标.22. 如图 (1)、【特例感知】如图23-1,对于抛物线 , 下列结论正确的序号是
(1)、【特例感知】如图23-1,对于抛物线 , 下列结论正确的序号是①抛物线都经过点;
②抛物线的对称轴由拋物线的对称轴依次向左平移个单位得到;
③抛物线与直线的交点中,相邻两点之间的距离相等.
(2)、
【形成概念】把满足(为正整数)的抛物线称为“系列平移抛物线”.
【知识应用】在(2)中,如图.①“系列平移抛物线”的顶点依次为 , 用含n的代数式表示顶点Pn的坐标,并写出该顶点纵坐标y与横坐标x之间的关系式;
②“系列平移拔物线”存在“系列整数点(横、纵坐标均为整数的点)”: , , 其横坐标分别为:为正整数),判断相邻两点之间的距离是否都相等,若相等,请求出相邻两点之间的距离;若不相等,说明理由.
③在②中,直线分别交“系列平移抛物线”于点 , 连接 , 判断直线是否平行?请直接写出判断结果.