【提升卷】2.1二次函数—2023-2024学年北师大版九年级下册同步测试

试卷更新日期：2023-09-17 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列函数是二次函数的是（）

A、 $y = x + \frac{1}{3}$ B、 $y = a x^{2} + b x + c$ C、 $y = 3 {(x - 1)}^{2}$ D、 $y = 3 x$

查看试题解析
2. 下列各式中，y是x的二次函数的是（　　）

A、 $y \geq 3 x$ B、 $y = x^{2} + (3 - x) x$ C、 $y = (x - 1)^{2}$ D、 $y = a x^{2} + b x + c$

查看试题解析
3. 下列函数中（x，t是自变量），是二次函数的是（）

A、 $y = - x^{3} + 25$ B、 $y = - \frac{1}{2} + 5 x^{2}$ C、 $y = \frac{1}{x}$ D、 $S = 1 + t$

查看试题解析
4. 已知函数 $y = (m + 3) x^{2} + 1$ 是二次函数，则m的取值范围为（）

A、 $m > - 3$ B、 $m < - 3$ C、 $m \neq - 3$ D、任意实数

查看试题解析
5. 若y＝ $(m - 1) x^{m^{2} + 1}$ 是二次函数，则m的值是（）

A、﹣1 B、1 C、1或﹣1 D、2

查看试题解析
6. 已知 $y$ 关于 $x$ 的二次函数解析式为 $y = (m - 2) x^{| m |}$ ，则 $m =$ （）

A、±2 B、1 C、-2 D、±1

查看试题解析
7. 如果 $y = (m - 2) x^{2} + (m - 1) x$ 是关于x的二次函数，则m的取值范围是（）

A、 $m \neq 1$ B、 $m \neq 2$ C、 $m \neq 2$ 且 $m \neq 1$ D、全体实数

查看试题解析
8. 下列具有二次函数关系的是（）

A、正方形的周长y与边长x B、速度一定时，路程s与时间t C、三角形的高一定时，面积y与底边长x D、正方形的面积y与边长x

查看试题解析
9. 某商品的进价为每件20元，现在的售价为每件40元，每星期可卖出200件．市场调查反映：如调整价格，每涨价1元，每星期要少卖出5件．则每星期售出商品的利润y（单位：元）与每件涨价x（单位：元）之间的函数关系式是（）

A、y＝（200﹣5x）（40﹣20＋x） B、y＝（200＋5x）（40﹣20﹣x） C、y＝200（40﹣20﹣x） D、y＝200﹣5x

查看试题解析
10. 如图，某农场拟建一间矩形奶牛饲养室，打算一边利用房屋现有的墙（墙足够长），其余三边除大门外用栅栏围成，栅栏总长度为50m，门宽为2m．若饲养室长为xm，占地面积为ym² ，则y关于x的函数表达式为（）

A、y=- $\frac{1}{2}$ x²+26x（2≤x＜52） B、y=- $\frac{1}{2}$ x²+50x（2≤x＜52） C、y=-x²+52x（2≤x＜52） D、y=- $\frac{1}{2}$ x²+27x-52（2≤x＜52）

查看试题解析

二、填空题（每题3分，共15分）

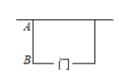
11. 若关于x的函数y＝（1﹣a）x²﹣x是二次函数，则a的取值范围是

查看试题解析
12. 若函数 $y = (m - 2) x^{m^{2} - 2 m + 2} - 6$ 是二次函数，则m的值为．

查看试题解析
13. 若二次函数 $y = m x^{2} + (2 m + n) x + 3 n$ 的二次项系数比一次项系数小12，一次项系数比常数项大8，则这个二次函数的解析式为.

查看试题解析
14. 如图，用长为16m的篱笆，一面利用墙（墙足够长）围成一块留有一扇1m宽的门的长方形花圃．设花圃的宽AB为xm，面积为ym² ，则y与x的函数表达式为．

查看试题解析
15. 中国“一带一路”倡议给沿线国家和地区带来很大的经济效益，沿线某地区居民2017年年人均收入300美元，预计2019年年人均收入将达到y美元．设2017年到2019年该地区居民年人均收入平均增长率为x，那么y与x的函数关系式是．

查看试题解析

三、解答题（共7题，共55分）

16. 当m为何值时，函数 $y = (m + 1) x^{m^{2} - 2 m - 1} + 8 x - 1$ 是二次函数．

查看试题解析
17. 已知函数y=（9k²﹣1）x²+2kx+3是关于x的二次函数，求不等式 $\frac{k - 1}{2} \geq \frac{4 k + 1}{3} - 1$ 的解集．

查看试题解析
18. 已知函数y=（m²﹣m）x²+（m﹣1）x+m+1．

(1)、若这个函数是一次函数，求m的值；

(2)、若这个函数是二次函数，则m的值应怎样？

查看试题解析
19. 写出下列函数的关系式：有一个角是60°的直角三角形的面积S与斜边x的之间的函数关系式．

查看试题解析
20. 如图，在△ABC中，∠C=90，AC=12cm，BC=24cm，动点P从点A开始沿边AC向点C以2cm/s的速度移动．动点Q从点B开始沿边BC向点C以4cm/s的速度移动，如果P、Q分别从点A、B同时出发，那么△PCQ的面积S随出发时间t如何变化？（写出函数关系式及t的取值范围）

查看试题解析
21. 为了改善小区环境，某小区决定要在一块一边靠墙（墙长25m）的空地上修建一条矩形绿化带ABCD，绿化带一边靠墙，另三边用总长为40m的栅栏围住（如图）．若设绿化带BC边长为xm，绿化带的面积为ym² ，求y与x之间的函数关系式，并写出自变量x的取值范围．

查看试题解析
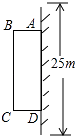22. 某商场经营某种品牌的玩具，购进时的价格是30元/件，根据市场调查：在一段时间内，当销售价格是40元/件时，销售量是600件．当销售单价每涨1元，就会少售出10件玩具．

销售价格(元/件)

x

销售量y(件)

销售玩具获得的利润w(元)

(1)、不妨设该种品牌玩具的销售价格为x元/件(x＞40)，请你分别用含x的代数式来表示销售量y件和销售该品牌玩具获得的利润w元，并把化简后的结果填写在表格中：

(2)、在第(1)问的条件下，若商场获得了10000元的销售利润，求该玩具的销售价格应定为多少元/件．

查看试题解析

销售价格(元/件)	x
销售量y(件)
销售玩具获得的利润w(元)