【提升卷】1.6利用三角函数测高—北师大版数学九年级下册同步测试
试卷更新日期:2023-09-17 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 某大桥采用了低塔斜拉桥桥型(如图1),图2是从图1抽象出的平面图,假设站在桥上测得拉索与水平桥面的夹角是30°,拉索的坡度(或坡比) , 两拉索底端距离是18米,则立柱的高度是( )
 A、18米 B、米 C、米 D、9米2. 如图,数学兴趣小组用测角仪和皮尺测量一座信号塔的高度,信号塔对面有一座高15米的瞭望塔 , 测得瞭望塔底与信号塔底之间的距离为25米,若从瞭望塔顶部测得信号塔顶的仰角为 , 则信号塔的高为( )
A、18米 B、米 C、米 D、9米2. 如图,数学兴趣小组用测角仪和皮尺测量一座信号塔的高度,信号塔对面有一座高15米的瞭望塔 , 测得瞭望塔底与信号塔底之间的距离为25米,若从瞭望塔顶部测得信号塔顶的仰角为 , 则信号塔的高为( ) A、米 B、米 C、米 D、米3. 如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A处看乙楼楼顶B处仰角为 , 则甲楼高度为( )
A、米 B、米 C、米 D、米3. 如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A处看乙楼楼顶B处仰角为 , 则甲楼高度为( ) A、15米 B、米 C、米 D、米4. 如图,考古队在处测得古塔顶端的仰角为 , 斜坡的长为5米,坡度 , 长为6米,则古塔的高度为( )
A、15米 B、米 C、米 D、米4. 如图,考古队在处测得古塔顶端的仰角为 , 斜坡的长为5米,坡度 , 长为6米,则古塔的高度为( ) A、米 B、米 C、米 D、米5. 如图,某校教学楼与的水平间距 , 在教学楼的顶部点测得教学楼的顶部点的仰角为 , 测得教学楼的底部点的俯角为 , 则教学楼的高度是( )
A、米 B、米 C、米 D、米5. 如图,某校教学楼与的水平间距 , 在教学楼的顶部点测得教学楼的顶部点的仰角为 , 测得教学楼的底部点的俯角为 , 则教学楼的高度是( )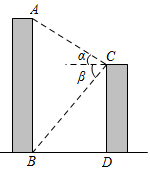 A、 B、 C、 D、6. 数学活动小组到某广场测量标志性建筑AB的高度.如图,他们在地面上C点测得最高点A的仰角为22°,再向前70m至D点,又测得最高点A的仰角为58°,点C,D,B在同一直线上,则该建筑物AB的高度约为( )(精确到1m.参考数据: , , , )
A、 B、 C、 D、6. 数学活动小组到某广场测量标志性建筑AB的高度.如图,他们在地面上C点测得最高点A的仰角为22°,再向前70m至D点,又测得最高点A的仰角为58°,点C,D,B在同一直线上,则该建筑物AB的高度约为( )(精确到1m.参考数据: , , , )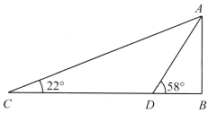 A、28m B、34m C、37m D、46m7. 某学校安装红外线体温检测仪(如图1),其红外线探测点O可以在垂直于地面的支杆OP上自由调节(如图2).已知最大探测角∠OBC=67°,最小探测角∠OAC=37°.测温区域AB的长度为2米,则该设备的安装高度OC应调整为( )米.(精确到0.1米.参考数据: , , , , , )
A、28m B、34m C、37m D、46m7. 某学校安装红外线体温检测仪(如图1),其红外线探测点O可以在垂直于地面的支杆OP上自由调节(如图2).已知最大探测角∠OBC=67°,最小探测角∠OAC=37°.测温区域AB的长度为2米,则该设备的安装高度OC应调整为( )米.(精确到0.1米.参考数据: , , , , , )
 A、2.4 B、2.2 C、3.0 D、2.78. 如图,小刚要测量斜坡CD旁一颗树AB的高度,已知在坡脚C处测得树顶B的仰角为 , 在坡顶D测得树顶B的仰角为 , 若 , , 则树AB的高是( )
A、2.4 B、2.2 C、3.0 D、2.78. 如图,小刚要测量斜坡CD旁一颗树AB的高度,已知在坡脚C处测得树顶B的仰角为 , 在坡顶D测得树顶B的仰角为 , 若 , , 则树AB的高是( ) A、5m B、 C、15m D、10m9. 如图,AB是垂直于水平面的建筑物,沿建筑物底端B沿水平方向向左走8米到达点C,沿坡度i=1:2(坡度i=坡面铅直高度与水平宽度的比)斜坡走到点D,再继续沿水平方向向左走40米到达点E(A、B、C、D、E在同一平面内),在E处测得建筑物顶端A的仰角为34°,已知建筑物底端B与水平面DE的距离为2米,则建筑物AB的高度约是( )(参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
A、5m B、 C、15m D、10m9. 如图,AB是垂直于水平面的建筑物,沿建筑物底端B沿水平方向向左走8米到达点C,沿坡度i=1:2(坡度i=坡面铅直高度与水平宽度的比)斜坡走到点D,再继续沿水平方向向左走40米到达点E(A、B、C、D、E在同一平面内),在E处测得建筑物顶端A的仰角为34°,已知建筑物底端B与水平面DE的距离为2米,则建筑物AB的高度约是( )(参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67) A、27.1米 B、30.8米 C、32.8米 D、49.2米10. 如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为60°,建筑物底端B的俯角为45°,点A、B、C、D、E在同一平面内,斜坡AD的坡度 . 根据小颖的测量数据,计算出建筑物BC的高度约为( )(参考数据:)
A、27.1米 B、30.8米 C、32.8米 D、49.2米10. 如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为60°,建筑物底端B的俯角为45°,点A、B、C、D、E在同一平面内,斜坡AD的坡度 . 根据小颖的测量数据,计算出建筑物BC的高度约为( )(参考数据:)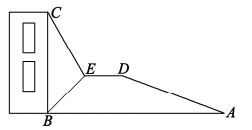 A、136.6米 B、86.7米 C、186.7米 D、86.6米
A、136.6米 B、86.7米 C、186.7米 D、86.6米二、填空题(每题3分,共15分)
-
11. 在一次综合实践活动中,某学校数学兴趣小组对一电视发射塔的高度进行了测量.如图,在塔前C处,测得该塔顶端B的仰角为 , 后退()到D处有一平台,在高()的平台上的E处,测得B的仰角为 . 则该电视发射塔的高度为 . (精确到 . 参考数据:)
 12. 如图,某校数学兴趣小组的同学测量校园内一棵树DE的高度,他们在这棵树的正前方一旗台的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度 , 台阶AC的坡度为 , 且B,C,E三点在同一直线上,则树高DE为m.(测倾器的高度忽略不计)
12. 如图,某校数学兴趣小组的同学测量校园内一棵树DE的高度,他们在这棵树的正前方一旗台的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度 , 台阶AC的坡度为 , 且B,C,E三点在同一直线上,则树高DE为m.(测倾器的高度忽略不计) 13. 小红同学在数学活动课中测量旗杆的高度,如图,已知测角仪的高度为1.58米,她在点观测旗杆顶端的仰角为 , 接着朝旗杆方向前进20米到达处,在点观测旗杆顶端的仰角为 , 则旗杆的高度为 米结果保留小数点后一位,参考数据:
13. 小红同学在数学活动课中测量旗杆的高度,如图,已知测角仪的高度为1.58米,她在点观测旗杆顶端的仰角为 , 接着朝旗杆方向前进20米到达处,在点观测旗杆顶端的仰角为 , 则旗杆的高度为 米结果保留小数点后一位,参考数据: 14. 如图.某同学为测量宣传牌的高度 , 他站在距离教学楼底部E处9米远的地面C处,测得宣传牌的底部B的仰角为60°,同时测得教学楼窗户D处的仰角为30°(A、B、D、E在同一直线上).然后,小明沿坡度的斜坡从C走到F处,此时正好与地面平行.他在F处又测得宣传牌顶部A的仰角为45°,则宣传牌的高度(结果保留根号).
14. 如图.某同学为测量宣传牌的高度 , 他站在距离教学楼底部E处9米远的地面C处,测得宣传牌的底部B的仰角为60°,同时测得教学楼窗户D处的仰角为30°(A、B、D、E在同一直线上).然后,小明沿坡度的斜坡从C走到F处,此时正好与地面平行.他在F处又测得宣传牌顶部A的仰角为45°,则宣传牌的高度(结果保留根号).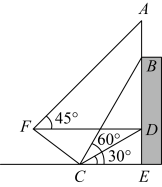 15. 如图,某人在山坡坡脚 处测得电视塔尖点 的仰角为 , 沿山坡向上走到 处再测得点 的仰角为 , 已知 米,山坡坡度为 , 且 , , 在同一条直线上,则此人所在位置点 的铅直高度为米.
15. 如图,某人在山坡坡脚 处测得电视塔尖点 的仰角为 , 沿山坡向上走到 处再测得点 的仰角为 , 已知 米,山坡坡度为 , 且 , , 在同一条直线上,则此人所在位置点 的铅直高度为米.
三、解答题(共7题,共55分)
-
16. 永州市道县陈树湘纪念馆中陈列的陈树湘雕像高2.9米(如图1所示),寓意陈树湘为中国革命“断肠明志”牺牲时的年龄为29岁.如图2,以线段代表陈树湘雕像,一参观者在水平地面上D处为陈树湘雕拍照,相机支架高0.9米,在相机C处观测雕像顶端A的仰角为 , 然后将相机架移到处拍照,在相机M处观测雕像顶端A的仰角为 , 求D、N两点间的距离(结果精确到0.1米,参考数据:)
 17. 文昌阁位于河南省辉县市区,创建于明代,为八角形三层攒尖顶阁楼,砖木结构.文昌阁是河南省第五批文物保护单位,其建筑结构严谨,造型精巧,工艺精致,气势宏伟,体量高大,是明代木构阁楼建筑的精华,具有重要的历史、科学、艺术价值.某数学兴趣小组准备测量文昌阁阁身的高度,为此制订了测量方案,并利用周末完成了测量,测量结果如下表:
17. 文昌阁位于河南省辉县市区,创建于明代,为八角形三层攒尖顶阁楼,砖木结构.文昌阁是河南省第五批文物保护单位,其建筑结构严谨,造型精巧,工艺精致,气势宏伟,体量高大,是明代木构阁楼建筑的精华,具有重要的历史、科学、艺术价值.某数学兴趣小组准备测量文昌阁阁身的高度,为此制订了测量方案,并利用周末完成了测量,测量结果如下表:活动课题
测量文昌阁阁身的高度
活动目的
运用三角函数知识解决实际问题
活动工具
测角仪、皮尺等测量工具
示意图

测量步骤
如上图:①利用测角仪在台阶D处测得文昌阁顶点A的仰角为45°;
②利用测角仪在台阶C处测得的文昌阁顶点A的仰角为57°;
③利用皮尺测量每个台阶的高度计算出两处台阶的高度均为1.8m(即点B和点C,点C和点D的垂直距离均为1.8m),利用皮尺测量每个台阶的宽度及点C和点D到台阶边缘的距离计算出点C和点D的水平距离为6.6m(已知A、B、C、D、E均在同一平面内)
请运用所学知识,根据上表中的数据,计算文昌阁阁身AB的高度。(结果取整数.参考数据:sin57°≈0.84,cos57°≈0.54,tan57°≈1.54)
18. 某校“综合与实践”活动小组的同学要测量两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在两楼之间上方的点O处,点O距地面的高度为 , 此时观测到楼底部点A处的俯角为 , 楼上点E处的俯角为 , 沿水平方向由点O飞行到达点F , 测得点E处俯角为 , 其中点A , B , C , D , E , F , O均在同一竖直平面内.(参考数据: , , , ) (1)、求的长;(2)、求楼与之间的距离的长.19. 某校九年级四个数学活动小组参加测量旗杆高度的综合实践活动.如图是四个小组测量的示意图,用测角仪测得杆顶端A的仰角记为 , 为测角仪的高,测角仪的底部C处与旗杆的底部B处之间的距离记为 , 四个小组的测量位置略有不同,测量和计算的数据如下表所示:
(1)、求的长;(2)、求楼与之间的距离的长.19. 某校九年级四个数学活动小组参加测量旗杆高度的综合实践活动.如图是四个小组测量的示意图,用测角仪测得杆顶端A的仰角记为 , 为测角仪的高,测角仪的底部C处与旗杆的底部B处之间的距离记为 , 四个小组的测量位置略有不同,测量和计算的数据如下表所示:组别
的长/m
的长/m
仰角
的长/m

第一组
1.59
13.2
9.8
第二组
1.58
13.4
9.6
第三组
1.57
14.1
9.7
第四组
1.56
15.2
(1)、利用第四组学生测量的数据,求旗杆的高度;(2)、四组学生测量旗杆高度的平均值约为多少米?(结果精确到0.1m;参考数据:)
(3)、请对本次实践活动进行评价(写出一条即可).20. 为为加强对市内道路交通安全的监督,王警官利用无人机进行检测.某高架路有一段限速每小时60千米的道路AB(如图所示),当无人机在限速道路的正上方C处时,测得限速道路的起点A的俯角是37°,无人机继续向右水平飞行220米到达D处,此时又测得起点A的俯角是30°,同时测得限速道路终点B的俯角是45°(注:即四边形ABDC是梯形).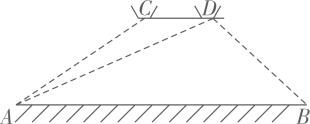 (1)、求限速道路AB的长(精确到1米);(2)、如果李师傅在道路AB上行驶的时间是1分20秒,请判断他是否超速?并说明理由.
(1)、求限速道路AB的长(精确到1米);(2)、如果李师傅在道路AB上行驶的时间是1分20秒,请判断他是否超速?并说明理由.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,)
21. (阅读材料)某校九年级数学课外兴趣探究小组在学习完《第二十八章锐角三角函数》后,利用所学知识进行深度探究,得到以下正确的等量关系式:,
,
, ,
 (1)、(理解应用)请你利用以上信息求下列各式的值:
(1)、(理解应用)请你利用以上信息求下列各式的值:;
(2)、(3)、(拓展应用)为了求出海岛上的山峰 的高度,在 处和 处树立标杆 和 ,标杆的高都是3丈, 两处相隔1000步(1步等于6尺),并且 和 在同一平面内,在标杆 的顶端 处测得山峰顶端 的仰角75°,在标杆 的顶端 处测得山峰顶端 的仰角30°,山峰的高度即 的长是多少步?(结果保留整数)(参考数据: )
22. 阅读材料:关于三角函数还有如下的公式:
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值.
例:
=
=
=
=
= =
根据以上阅读材料,请选择适当的公式解答下面问题
(1)、计算:sin15°;(2)、乌蒙铁塔是六盘水市标志性建筑物之一(图1),小华想用所学知识来测量该铁塔的高度,如图2,小华站在离塔底A距离7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.62米,请帮助小华求出乌蒙铁塔的高度.(精确到0.1米,参考数据 )