【培优卷】1.6利用三角函数测高—北师大版数学九年级下册同步测试
试卷更新日期:2023-09-17 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 小杰在一个高为的建筑物顶端,测得一根高出此建筑物的旗杆顶端的仰角为 , 旗杆与地面接触点的俯角为 , 那么该旗杆的高度是( )A、 B、 C、 D、2. 如图,甲、乙为两座建筑物,它们之间的水平距离为 , 在A点测得D点的仰角为 , 在B点测得D点的仰角为 , 则乙建筑物的高度为( )
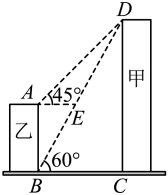 A、 B、 C、 D、3. 小明去爬山,在山脚A看山顶D的仰角 , 小明在坡比为的山坡上走1300米到达B处,此时小明看山顶的仰角 , 则山高为( )米
A、 B、 C、 D、3. 小明去爬山,在山脚A看山顶D的仰角 , 小明在坡比为的山坡上走1300米到达B处,此时小明看山顶的仰角 , 则山高为( )米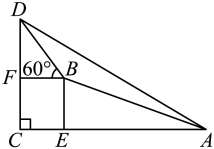 A、 B、 C、 D、4. 为测量此塔顶的高度,在地面选取了与塔底共线的两点、 , 、在的同侧,在处测量塔顶的仰角为 , 在处测量塔顶的仰角为 , 到的距离是89.5米.设的长为米,则下列关系式正确的是( )
A、 B、 C、 D、4. 为测量此塔顶的高度,在地面选取了与塔底共线的两点、 , 、在的同侧,在处测量塔顶的仰角为 , 在处测量塔顶的仰角为 , 到的距离是89.5米.设的长为米,则下列关系式正确的是( ) A、 B、 C、 D、5. 为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)=1:2.4的山坡AB上发现有一棵占树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为( )(参考数据:°≈0.73,cos8°≈0.67,tan48°≈1.11)
A、 B、 C、 D、5. 为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)=1:2.4的山坡AB上发现有一棵占树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为( )(参考数据:°≈0.73,cos8°≈0.67,tan48°≈1.11)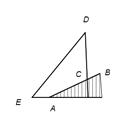 A、17.0米 B、21.9米 C、23.3米 D、33.3米6. 如图,为测量学校旗杆AB的高度,小明从旗杆正前方3米处的点C出发,沿坡度为的斜坡CD前进米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米,A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直,则旗杆AB的高度为( )(精确到0.1).(参考数据: , , , )
A、17.0米 B、21.9米 C、23.3米 D、33.3米6. 如图,为测量学校旗杆AB的高度,小明从旗杆正前方3米处的点C出发,沿坡度为的斜坡CD前进米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米,A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直,则旗杆AB的高度为( )(精确到0.1).(参考数据: , , , ) A、6.7 B、7.7 C、8.7 D、8.57. 如图,在阳光下直立于地面上的电线杆AB,落在水平面和坡面上的影子分别是BC、CD,测得米,米,斜坡CD的坡度为 , 在D处测电线杆顶端A的仰角为30°,则电线杆AB的高度为( )
A、6.7 B、7.7 C、8.7 D、8.57. 如图,在阳光下直立于地面上的电线杆AB,落在水平面和坡面上的影子分别是BC、CD,测得米,米,斜坡CD的坡度为 , 在D处测电线杆顶端A的仰角为30°,则电线杆AB的高度为( )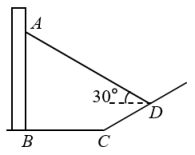 A、 B、 C、 D、8. 为了疫情防控工作的需要,某学校在门口的大门上方安装了人体体外测温摄像头,当学生站在点B时测得摄像头M的仰角为30°,当学生走到点A时测得摄像头M的仰角为60°,则当学生从B走向A时,测得的摄像头M的仰角为( )
A、 B、 C、 D、8. 为了疫情防控工作的需要,某学校在门口的大门上方安装了人体体外测温摄像头,当学生站在点B时测得摄像头M的仰角为30°,当学生走到点A时测得摄像头M的仰角为60°,则当学生从B走向A时,测得的摄像头M的仰角为( )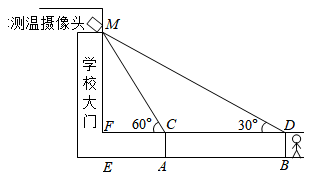 A、越来越小,可能为20° B、越来越大,可能为40° C、越来越大,可能为70° D、走到AB中点时,仰角一定为45°9. 电力公司在农村电网改造升级工程中把某一输电线铁塔建在了一个坡度为1:0.75的山坡的平台上(如图),测得 , 米,米,米,则铁塔的高度约为(参考数据: , , )( )
A、越来越小,可能为20° B、越来越大,可能为40° C、越来越大,可能为70° D、走到AB中点时,仰角一定为45°9. 电力公司在农村电网改造升级工程中把某一输电线铁塔建在了一个坡度为1:0.75的山坡的平台上(如图),测得 , 米,米,米,则铁塔的高度约为(参考数据: , , )( )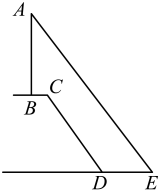 A、32.5米 B、27.5米 C、30.5米 D、58.5米10. 在数学实践活动课上,某兴趣小组测量操场上篮球筐距地面的高度如图所示,已知篮球筐的直径AB 约为0.45m,某同学站在C处,先仰望篮球筐直径的一端A处,测得仰角为42°,再调整视线,测得篮球筐直径的另一端B处的仰角为35°.若该同学的目高OC为1.7m,则篮球筐距地面的高度AD大约是( )m.(结果精确到1m).(参考数据:tan42°≈0.9,tan35°=0.7,tan48°≈1.1,tan55°≈1.4)
A、32.5米 B、27.5米 C、30.5米 D、58.5米10. 在数学实践活动课上,某兴趣小组测量操场上篮球筐距地面的高度如图所示,已知篮球筐的直径AB 约为0.45m,某同学站在C处,先仰望篮球筐直径的一端A处,测得仰角为42°,再调整视线,测得篮球筐直径的另一端B处的仰角为35°.若该同学的目高OC为1.7m,则篮球筐距地面的高度AD大约是( )m.(结果精确到1m).(参考数据:tan42°≈0.9,tan35°=0.7,tan48°≈1.1,tan55°≈1.4) A、2.5 B、2.6 C、2.8 D、3
A、2.5 B、2.6 C、2.8 D、3二、填空题(每题3分,共15分)
-
11. 小丽测量了斜坡上一棵垂直于地面的大树的高度.如图,小丽先在坡角为的斜坡上的点处,测得树尖的仰角为 , 然后沿斜坡走了10米到达坡脚处,又在水平路面上行走20米到达大树所在的斜坡坡脚处,大树所在斜坡的坡度 , 且大树与坡脚的距离为15米,则大树的高度约为 . 参考数据: , , , . (结果精确到0.1)
 12. 如图,一同学进行单摆运动实验,从A点出发,在右侧达到最高点B.实验过程中在O点正下方的P处有一个钉子.已知在O点测得起始位置A的俯角是 , B点的俯角是 , B点测得钉子P的仰角是 , 且长为4,则摆绳长为 .
12. 如图,一同学进行单摆运动实验,从A点出发,在右侧达到最高点B.实验过程中在O点正下方的P处有一个钉子.已知在O点测得起始位置A的俯角是 , B点的俯角是 , B点测得钉子P的仰角是 , 且长为4,则摆绳长为 . 13. 如图,某科技兴趣小组在操场上活动,此时无人机在离地面的点D处,无人机测得操控者A的俯角为 , 测得点C处的俯角为.又经过人工测量操控者A和教学楼之间的水平距离为 , 教学楼的高度m.(注:点A,B,C,D在同一平面上,参考数据: , 结果保留整数)
13. 如图,某科技兴趣小组在操场上活动,此时无人机在离地面的点D处,无人机测得操控者A的俯角为 , 测得点C处的俯角为.又经过人工测量操控者A和教学楼之间的水平距离为 , 教学楼的高度m.(注:点A,B,C,D在同一平面上,参考数据: , 结果保留整数) 14. 如图,一同学进行单摆运动实验,从A点出发,在右侧达到最高点B.实验过程中在О点正下方的P处有一个钉子.已知在О点测得起始位置A的俯角是45°,B点的俯角是60°,B点测得钉子P的仰角是45°,且OP长为4,则摆绳OA长为.
14. 如图,一同学进行单摆运动实验,从A点出发,在右侧达到最高点B.实验过程中在О点正下方的P处有一个钉子.已知在О点测得起始位置A的俯角是45°,B点的俯角是60°,B点测得钉子P的仰角是45°,且OP长为4,则摆绳OA长为. 15. 某体育看台侧面的示意图如图所示,观众区 的坡度 为 ,顶端 离水平地面 的高度为 ,从顶棚的 处看 处的仰角 ,竖直的立杆上 、 两点间的距离为 , 处到观众区底端 处的水平距离 为 .则观众区的水平宽度 ;顶棚的 处离地面的高度 .( , ,结果精确到 )
15. 某体育看台侧面的示意图如图所示,观众区 的坡度 为 ,顶端 离水平地面 的高度为 ,从顶棚的 处看 处的仰角 ,竖直的立杆上 、 两点间的距离为 , 处到观众区底端 处的水平距离 为 .则观众区的水平宽度 ;顶棚的 处离地面的高度 .( , ,结果精确到 )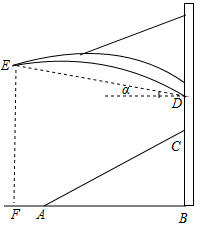
三、解答题(共7题,共55分)
-
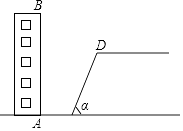
16. 如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81, ≈1.41, ≈1.73, ≈2.24)
 17. 货车长方体货厢的净高BC为2.5 m,底部B离地面的高度BD为1.2 m.现欲将高为2 m的正方体货物装进货厢,工人师傅搭了坡度为i=1∶3的坡面AB.
17. 货车长方体货厢的净高BC为2.5 m,底部B离地面的高度BD为1.2 m.现欲将高为2 m的正方体货物装进货厢,工人师傅搭了坡度为i=1∶3的坡面AB. (1)、若货物从如图所示的位置升高0.5 m,则水平移动了多少?(2)、由于货物较重但分布均匀,工人师傅试图将货物沿坡面AB推到适当位置后,再轻松平放进货厢.请问能否达到目的?为什么?18. 某综合实践研究小组为了测量观察目标时的仰角和俯角,利用量角器和铅锤自制了一个简易测角仪,如图1所示.
(1)、若货物从如图所示的位置升高0.5 m,则水平移动了多少?(2)、由于货物较重但分布均匀,工人师傅试图将货物沿坡面AB推到适当位置后,再轻松平放进货厢.请问能否达到目的?为什么?18. 某综合实践研究小组为了测量观察目标时的仰角和俯角,利用量角器和铅锤自制了一个简易测角仪,如图1所示. (1)、如图2,在点观察所测物体最高点 , 当量角器零刻度线上两点均在视线上时,测得视线与铅垂线所夹的锐角为 , 设仰角为 , 请直接用含的代数式示 .(2)、如图3,为了测量广场上空气球离地面的高度,该小组利用自制简易测角仪在点分别测得气球的仰角为 , 为 , 地面上点在同一水平直线上, , 求气球离地面的高度 . (参考数据: , )19. 如图①, 、 是两座垂直于同一水平地面且高度不同的铁塔.小明和小丽为了测量两座铁塔的高度,从地面上的点 处测得铁塔顶端 的仰角为39°,铁塔顶端 的仰角为27°,沿着 向前走20米到达点 处,测得铁塔顶端 的仰角为53°.已知 ,点 、 、 构成的 中, .
(1)、如图2,在点观察所测物体最高点 , 当量角器零刻度线上两点均在视线上时,测得视线与铅垂线所夹的锐角为 , 设仰角为 , 请直接用含的代数式示 .(2)、如图3,为了测量广场上空气球离地面的高度,该小组利用自制简易测角仪在点分别测得气球的仰角为 , 为 , 地面上点在同一水平直线上, , 求气球离地面的高度 . (参考数据: , )19. 如图①, 、 是两座垂直于同一水平地面且高度不同的铁塔.小明和小丽为了测量两座铁塔的高度,从地面上的点 处测得铁塔顶端 的仰角为39°,铁塔顶端 的仰角为27°,沿着 向前走20米到达点 处,测得铁塔顶端 的仰角为53°.已知 ,点 、 、 构成的 中, .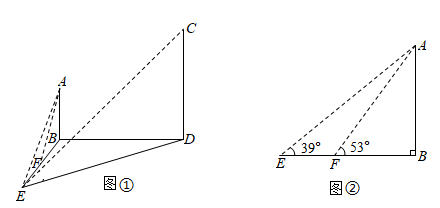
(参考数据: , , , , , , , , )
(1)、图②是图①中的一部分,求铁塔 的高度;(2)、小明说,在点 处只要再测量一个角,通过计算即可求出铁塔 的高度,那么可以测量的角是 , 若将这个角记为 ,则铁塔 的高度是;(用含 的式子表示)(3)、小丽说,除了在点 处测量角的度数外,还可以在点 处再测量一条线段的长度,通过计算也可求出铁塔 的高度,那么可以测量的线段是.(请写出两个不同的答案,可用文字描述)20. 关于三角函数有如下的公式:sin(α+β)=sinαcosβ+cosαsinβ①
cos(α+β)=cosαcosβ﹣sinαsinβ②
tan(α+β)= ③
利用这些公式可将某些不是特殊角的三角函数转化为特殊角的三角函数来求值,如:
tan105°=tan(45°+60°)= =﹣(2+ ).
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
如图,直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α=60°,底端C点的俯角β=75°,此时直升飞机与建筑物CD的水平距离BC为42m,求建筑物CD的高.
 21. 【阅读材料】关于三角函数有如下的公式:①;②;③.利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值,如.
21. 【阅读材料】关于三角函数有如下的公式:①;②;③.利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值,如.【学以致用】根据上面的知识,你可以选择适当的公式解决下面的实际问题:
 (1)、求的值;(2)、如图,一架直升机在一建筑物上方的点A处测得建筑物顶端点D的俯角为 , 底端点C的俯角为 , 此时直升机与建筑物的水平距离为 , 求建筑物的高;(3)、疫情封控期间,直升机给该建筑物的居民投放物资,试求飞机从点A处往正东方向飞多远,居民在点D处看飞机的仰角恰好是.22. 综合与实践
(1)、求的值;(2)、如图,一架直升机在一建筑物上方的点A处测得建筑物顶端点D的俯角为 , 底端点C的俯角为 , 此时直升机与建筑物的水平距离为 , 求建筑物的高;(3)、疫情封控期间,直升机给该建筑物的居民投放物资,试求飞机从点A处往正东方向飞多远,居民在点D处看飞机的仰角恰好是.22. 综合与实践[问题情境]学习完《解直角三角形的应用》后,同学们对如何建立解直角三角形的模型测量物体的实际高度产生了浓厚的兴趣,数学老师决定开展一次主题为《测量学校旗杆高度》的数学实践活动,并为各小组准备了卷尺、测角仪等工具,要求各小组建立测高模型并测量学校旗杆的高度.
[问题探究]第一小组的同学经过讨论,制定出了如下测量实施方案:
第一步,建立测高模型,画出测量示意图(如图1),明确需要测量的数据和测量方法:用卷尺测量测角仪CD的高度和测角仪底部C与旗杆底部A之间的距离,用测角仪测量旗杆顶端B的仰角;
第二步,进行组员分工,制作测量数据记录表;
第三步,选择不同的位置测量三次,依次记录测量数据;
第四步,整理数据,计算旗杆的高,撰写研究报告.
如表是该组同学研究报告中的数据记录和计算结果:
测量组别
的长(米)
的长(米)
仰角
计算的高(米)
位置1
位置2
位置3
平均值
研究结论:旗杆的高为n米
 (1)、表中n的值为;该小组选择不同的位置测量三次,再以三次测量计算的旗杆高度的平均数作为研究结论,这样做的目的是.(2)、该测量模型中,若 , 仰角为 , 用含的代数式表示旗杆的高度为.(3)、[拓展应用]第二小组同学设计的是另外一种测量方案,他们画出的测量示意图如图2,测量时,固定测角仪的高度为m,先在点C处测得旗杆顶端B的仰角 , 然后朝旗杆方向前进m到达点H处,再次测得旗杆顶端B的仰角 , 请你帮他们求出旗杆的高度(结果保留根号).
(1)、表中n的值为;该小组选择不同的位置测量三次,再以三次测量计算的旗杆高度的平均数作为研究结论,这样做的目的是.(2)、该测量模型中,若 , 仰角为 , 用含的代数式表示旗杆的高度为.(3)、[拓展应用]第二小组同学设计的是另外一种测量方案,他们画出的测量示意图如图2,测量时,固定测角仪的高度为m,先在点C处测得旗杆顶端B的仰角 , 然后朝旗杆方向前进m到达点H处,再次测得旗杆顶端B的仰角 , 请你帮他们求出旗杆的高度(结果保留根号).