【基础卷】1.6利用三角函数测高—2023-2024学年北师大版九年级下册同步测试

试卷更新日期：2023-09-17 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 某斜坡的坡度 $i = 1 ： \sqrt{3}$ ，则该斜坡的坡角为（　　）

A、75° B、60° C、45° D、30°

查看试题解析
2. 一个钢球沿坡角31°的斜坡向上滚动了5米，此时钢球距地面的高度是（单位：米）（）

A、 $5 c o s 31 °$ B、 $5 s i n 31 °$ C、 $\frac{5}{s i n 31 °}$ D、 $5 t a n 31 °$

查看试题解析
3. 一小球从斜坡的顶端沿斜坡向下滚落到斜坡底端，行了100米，下落的铅直高度为50米，则该斜坡的坡度为（）

A、30° B、 $1 ： \sqrt{3}$ C、 $\sqrt{3}$ D、 $\frac{1}{2}$

查看试题解析
4. 如图，坡角为α的斜坡上有一棵垂直于水平地面的大树AB，当太阳光线与水平线成45°角沿斜坡照下，在斜坡上的树影BC长为m，则大树AB的高为（）

A、 $m (\cos α - \sin α)$ B、 $m (\sin α - \cos α)$ C、 $m (\cos α - \tan α)$ D、 $\frac{m}{\sin α} - \frac{m}{\cos α}$

查看试题解析
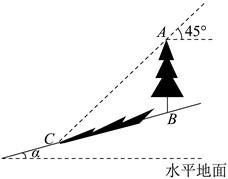5. 某商场准备改善原有楼梯的安全性能，把坡角由37°减至30°，已知原楼梯长为5米，调整后的楼梯会加长（）(参考数据： $\sin 37^{°} \approx \frac{3}{5}$ ， $\cos 37^{°} \approx \frac{4}{5} ， \tan 37^{°} \approx \frac{3}{4}) .$

A、6米 B、3米 C、2米 D、1米

查看试题解析
6. “儿童放学归来早，忙趁东风放纸鸢”，小明周末在龙潭公园草坪上放风筝，已知风筝拉线长100米且拉线与地面夹角为 $65 °$ （如图所示，假设拉线是直的，小明身高忽略不计），则风筝离地面的高度可以表示为（）

A、 $100 s i n 65 °$ B、 $100 c o s 65 °$ C、 $100 t a n 65 °$ D、 $\frac{100}{s i n 65 °}$

查看试题解析
7. 如图，某数学活动小组要测量校园内旗杆 $A B$ 的高度，点B、C在同一条水平线上，测角仪在D处测得旗杆最高点A的仰角为 $α$ ．若测角仪 $C D = a$ ， $B C = b$ ，则旗杆 $A B$ 的高度为（）

A、 $a + b c o s α$ B、 $a + \frac{b}{c o s α}$ C、 $a + b t a n α$ D、 $a + \frac{b}{t a n α}$

查看试题解析
8. 如图，河堤横断面迎水坡AB的坡度是1：2，坡面AB= $6 \sqrt{5}$ ，则堤高的高度是（）

A、3 B、 $6 \sqrt{5}$ C、6 D、 $3 \sqrt{5}$

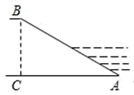查看试题解析
9. 如图，一枚运载火箭从地面L处发射，雷达站R与发射点L距离 $6 k m$ ，当火箭到达A点时，雷达站测得仰角为 $43 °$ ，则这枚火箭此时的高度 $A L$ 为（）

A、 $6 s i n 43 °$ B、 $6 c o s 43 °$ C、 $\frac{6}{t a n 43 °}$ D、 $6 t a n 43 °$

查看试题解析
10. 日照灯塔是日照海滨港口城市的标志性建筑之一，主要为日照近海及进出日照港的船舶提供导航服务．数学小组的同学要测量灯塔的高度，如图所示，在点B处测得灯塔最高点A的仰角 $∠ A B D = 45 °$ ，再沿 $B D$ 方向前进至C处测得最高点A的仰角 $∠ A C D = 60 °$ ， $B C = 15.3 m$ ，则灯塔的高度 $A D$ 大约是（）（结果精确到 $1 m$ ，参考数据： $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ）

A、 $31 m$ B、 $36 m$ C、 $42 m$ D、 $53 m$

查看试题解析

二、填空题（每题3分，共15分）

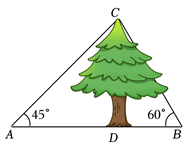
11. 如图，某数学兴趣小组测量一棵树CD的高度，在点A处测得树顶C的仰角为45°，在点B处测得树顶C的仰角为60°，且A，B，D三点在同一直线上，若AB＝20m，则这棵树CD的高度约为 m．（按四舍五入法将结果保留小数点后一位，参考数据： $\sqrt{3} \approx 1.732$ ）

查看试题解析
12. 如图，无人机在空中A处测得某校旗杆顶部B的仰角为30^o ，底部C的俯角为60^o ，无人机与旗杆的水平距离AD为6m，则该校的旗杆高约为m．（ $\sqrt{3} \approx 1.73$ ，结果精确到0.1）

查看试题解析
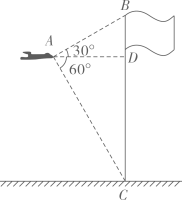13. 2023年岳阳举办以“跃马江湖”为主题的马拉松赛事．如图，某校数学兴趣小组在 $A$ 处用仪器测得赛场一宣传气球顶部 $E$ 处的仰角为 $21.8 °$ ，仪器与气球的水平距离 $B C$ 为20米，且距地面高度 $A B$ 为1.5米，则气球顶部离地面的高度 $E C$ 是米（结果精确到0.1米， $s i n 21.8 ° \approx 0.3714 ， c o s 21.8 ° \approx 0.9285 ， t a n 21.8 ° \approx 0.4000$ ）．

查看试题解析
14. 2022年，北京成功举办第24届冬季奥运会后，很多学校都开展了冰雪项目的学习活动．如图，一位同学乘滑雪板沿坡度为 $i = 3 ： 4$ 的斜坡滑行30米，则他下降的高度为米．

查看试题解析
15. 如图，传送带和地面所成斜坡的坡度为 $1 ： 4$ ，若它把物体从地面点 $A$ 处送到离地面 $1$ 米高的 $B$ 处，则物体从 $A$ 到 $B$ 所经过的路程为米．

查看试题解析

三、解答题（共7题，共55分）

16. 如图，粮库用传送带传送粮袋，大转动轮的半径为10cm，传送带与水平面成 $30 °$ 角．假设传送带与转动轮之间无滑动，当大转动轮转 $140 °$ 时，传送带上点 $A$ 处的粮袋上升的高度是多少？（传送带厚度忽略不计）

查看试题解析
17. 小华想利用太阳光测量楼 $A B$ 的高，他带着尺子来到楼下，发现地面和对面斜坡（坡角为45°）上都有这栋楼的影子，针对这种情况，他设计了一种测量方案，具体测量情况如下：先测得在此时刻1.2m高的物体垂直于地面放置时，影长是1m；楼 $A B$ 落在地面上的影长 $A D = 20 m$ ，落在斜坡上的影长 $C D = 12 m$ ，请你帮小华求出楼 $A B$ 的高.

查看试题解析
18. 如图所示是消防员攀爬云梯到小明家的场景．已知 $A E ⊥ B E ， B C ⊥ B E ， C D ∥ B E$ ， $A C = 10.4 m ， B C = 1.26 m$ ，点 $A$ 关于点 $C$ 的仰角为 $70 °$ ，则楼 $A E$ 的高度为多少 $m$ ？（结果保留整数．参考数据： $s i n 70 ° \approx 0.94 ， c o s 70 ° \approx 0.34 ， t a n 70 ° \approx 2.75$ ）

查看试题解析
19. “游张家界山水，逛七十二奇楼”成为今年旅游新特色．某数学兴趣小组用无人机测量奇楼 $A B$ 的高度，测量方案如图：先将无人机垂直上升至距水平地面225m的P点，测得奇楼顶端A的俯角为 $15 °$ ，再将无人机沿水平方向飞行200m到达点Q，测得奇楼底端B的俯角为 $45 °$ ，求奇楼 $A B$ 的高度．（结果精确到1m，参考数据： $s i n 15 ° \approx 0.26$ ， $c o s 15 ° \approx 0.97$ ， $t a n 15 ° \approx 0.27$ ）

查看试题解析
20. 我国航天事业捷报频传，2023年5月30日，被誉为“神箭”的长征二号F运载火箭托举神舟十六号载人飞船跃入苍穹中国空间站应用与发展阶段首次载人发射任务取得圆满成功，如图（九），有一枚运载火箭从地面 $O$ 处发射，当火箭到达 $P$ 处时，地面 $A$ 处的雷达站测得 $A P$ 距离是 $5000 m$ ，仰角为 $23 °$ ． $9 s$ ，火箭直线到达 $Q$ 处，此时地面 $A$ 处雷达站测得 $Q$ 处的仰角为 $45 °$ ．求火箭从 $P$ 到 $Q$ 处的平均速度（结果精确到 $1 m / s$ ）．（参考数据： $s i n 23 ° \approx 0.39 ， c o s 23 ° \approx 0.92 ， t a n 23 ° \approx 0.42$ ）

查看试题解析
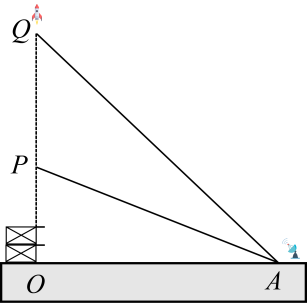21. 暑假期间，小明与小亮相约到某旅游风景区登山，需要登顶 $600 m$ 高的山峰，由山底A处先步行 $300 m$ 到达 $B$ 处，再由 $B$ 处乘坐登山缆车到达山顶 $D$ 处．已知点A，B．D，E，F在同一平面内，山坡 $A B$ 的坡角为 $30 °$ ，缆车行驶路线 $B D$ 与水平面的夹角为 $53 °$ （换乘登山缆车的时间忽略不计）

(1)、求登山缆车上升的高度 $D E$ ；

(2)、若步行速度为 $30 m / m i n$ ，登山缆车的速度为 $60 m / m i n$ ，求从山底A处到达山顶 $D$ 处大约需要多少分钟（结果精确到 $0.1 m i n$ ）
（参考数据： $s i n 53 ° \approx 0.80 ， c o s 53 ° \approx 0.60 ， t a n 53 ° \approx 1.33$ ）

查看试题解析
22. 小亮利用所学的知识对大厦的高度 $C D$ 进行测量，他在自家楼顶B处测得大厦底部的俯角是 $30 °$ ，测得大厦顶部的仰角是 $37 °$ ，已知他家楼顶B处距地面的高度 $B A$ 为40米（图中点A ， B ， C ， D均在同一平面内）．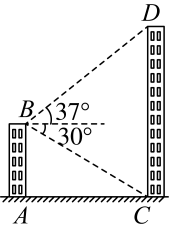

(1)、求两楼之间的距离 $A C$ （结果保留根号）；

(2)、求大厦的高度 $C D$ （结果取整数）．
（参考数据： $s i n 37 ° \approx 0.60$ ， $c o s 37 ° \approx 0.80$ ， $t a n 37 ° \approx 0.75$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析