【提升卷】1.5三角函数的应用—北师大版数学九年级下册同步测试
试卷更新日期:2023-09-17 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,一把梯子斜靠在墙上,端点A离地面的高度长为时,.当梯子底端点B沿水平方向向左移动到点 , 端点A沿墙竖直向上移动到点 , 设 , 则的长可以表示为( )
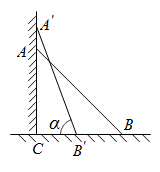 A、 B、 C、 D、2. 图1是一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形, , 则双翼边缘端点C与D之间的距离为( )
A、 B、 C、 D、2. 图1是一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形, , 则双翼边缘端点C与D之间的距离为( ) A、 B、 C、 D、3. 一配电房示意图如图所示,它是一个轴对称图形,已知 , , 则房顶A离地面的高度为( )
A、 B、 C、 D、3. 一配电房示意图如图所示,它是一个轴对称图形,已知 , , 则房顶A离地面的高度为( )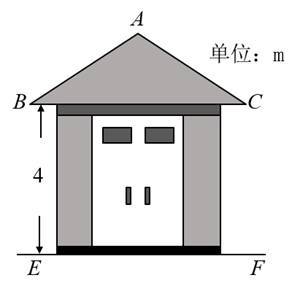 A、 B、 C、 D、4. 某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A、 B、 C、 D、4. 某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)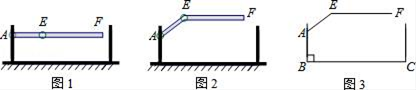 A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,直立于地面上的电线杆 , 在阳光下落在水平地面和坡面上的影子分别是、 , 坡面的坡度 , 测得米,米,在D处测得电线杆顶端A的仰角为 , 则电线杆的高度为( )米.
5. 如图,直立于地面上的电线杆 , 在阳光下落在水平地面和坡面上的影子分别是、 , 坡面的坡度 , 测得米,米,在D处测得电线杆顶端A的仰角为 , 则电线杆的高度为( )米. A、 B、 C、 D、6. 如图,这是某拦河坝改造前后河床的横断面示意图, , 坝高 , 将原坡度的迎水坡面改为坡角为的斜坡 , 此时,河坝面宽减少的长度等于( )(结果精确到 , 参考数据)
A、 B、 C、 D、6. 如图,这是某拦河坝改造前后河床的横断面示意图, , 坝高 , 将原坡度的迎水坡面改为坡角为的斜坡 , 此时,河坝面宽减少的长度等于( )(结果精确到 , 参考数据) A、 B、 C、 D、7. 如图2,在两建筑物之间有一旗杆,高15米,从点A经过旗杆顶点恰好可观测到矮建筑物的最底端点C处,从点A测得点C的俯角α为60°,测得点D的俯角β为30°,若旗杆底部G为BC的中点,则,矮建筑物的高CD为( )
A、 B、 C、 D、7. 如图2,在两建筑物之间有一旗杆,高15米,从点A经过旗杆顶点恰好可观测到矮建筑物的最底端点C处,从点A测得点C的俯角α为60°,测得点D的俯角β为30°,若旗杆底部G为BC的中点,则,矮建筑物的高CD为( ) A、18米 B、20米 C、10米 D、(45-15)米8. 在综合实践课上,某班同学测量校园内一棵树的高度.如图,测量仪在A处测得树顶D的仰角为45°,在C处测得树顶D的仰角为37°(点A、B、C在同一条水平主线上),已知测量仪的高度米,米,则树BD的高度是( )【参考数据: , , 】
A、18米 B、20米 C、10米 D、(45-15)米8. 在综合实践课上,某班同学测量校园内一棵树的高度.如图,测量仪在A处测得树顶D的仰角为45°,在C处测得树顶D的仰角为37°(点A、B、C在同一条水平主线上),已知测量仪的高度米,米,则树BD的高度是( )【参考数据: , , 】 A、12米 B、12.65米 C、13米 D、13.65米9. 如图,小明在C处看到西北方向上有一凉亭A,北偏东35°的方向上有一棵大树B,已知凉亭A在大树B的正西方向,若米,则AB的长等于( )
A、12米 B、12.65米 C、13米 D、13.65米9. 如图,小明在C处看到西北方向上有一凉亭A,北偏东35°的方向上有一棵大树B,已知凉亭A在大树B的正西方向,若米,则AB的长等于( )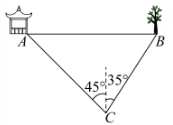 A、 B、 C、 D、10. 某驱逐舰在海上执行任务后刚返回到港口A,接到上级指令,发现在其北偏东方向上有一艘可疑船只C,与此同时在港口A处北偏东方向上且距离处有另一艘驱逐舰B也收到了相关指令,驱逐舰B恰好在可疑船只C的南偏东的方向上,则可疑船只C距离港口A的距离为( )
A、 B、 C、 D、10. 某驱逐舰在海上执行任务后刚返回到港口A,接到上级指令,发现在其北偏东方向上有一艘可疑船只C,与此同时在港口A处北偏东方向上且距离处有另一艘驱逐舰B也收到了相关指令,驱逐舰B恰好在可疑船只C的南偏东的方向上,则可疑船只C距离港口A的距离为( )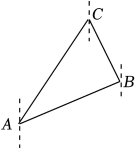 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共15分)
-
11. 一艘在南北航线上的测量船,在点A处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达点C时,测得海岛B在点C的北偏东45°方向,那么海岛B离此航线的最近距离是(结果保留整数).(参考数据: , )12. 如图,轮船B在码头A的正东方向,与码头A的距离为100海里,轮船B向北航行40海里到达C处时,接到D处一艘渔船发来的求救信号,于是沿北偏西45°方向航行到D处,解教渔船后轮船沿南偏西82°返回到码头A,那么码头A与D的距离为海里.(结果保留整数,参考数据: , , . )
 13. 综合实践课上,航模小组用航拍无人机进行测高实践.如图,无人机从地面的中点A处竖直上升30米到达B处,测得博雅楼顶部E的俯角为 , 尚美楼顶部F的俯角为 , 已知博雅楼高度为15米,则尚美楼高度为米.(结果保留根号)
13. 综合实践课上,航模小组用航拍无人机进行测高实践.如图,无人机从地面的中点A处竖直上升30米到达B处,测得博雅楼顶部E的俯角为 , 尚美楼顶部F的俯角为 , 已知博雅楼高度为15米,则尚美楼高度为米.(结果保留根号) 14. 某水上乐园在一平地推出了“急流勇进”的项目,项目有两条斜坡滑道以满足不同的难度需求,游客可以乘坐垂直升降电梯自由上下选择项目难度.其中斜坡轨道的坡度为 , 米,米,(其中点A、B、C、D均在同一平面内),则垂直升降电梯的高度约为米.(参考数据: , , )
14. 某水上乐园在一平地推出了“急流勇进”的项目,项目有两条斜坡滑道以满足不同的难度需求,游客可以乘坐垂直升降电梯自由上下选择项目难度.其中斜坡轨道的坡度为 , 米,米,(其中点A、B、C、D均在同一平面内),则垂直升降电梯的高度约为米.(参考数据: , , ) 15. 如图,某数学活动小组为测量学校旗杆AB的高度,从旗杆正前方米处的点C出发,沿斜面坡度的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB∥DE.旗杆AB的高度为米.(参考数据: . 计算结果保留根号)
15. 如图,某数学活动小组为测量学校旗杆AB的高度,从旗杆正前方米处的点C出发,沿斜面坡度的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB∥DE.旗杆AB的高度为米.(参考数据: . 计算结果保留根号)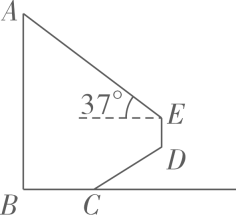
三、解答题(共7题,共55分)
-
16. 小王同学学习了锐角三角函数后,通过观察广场的台阶与信号塔之间的相对位置,他认为利用台阶的可测数据与在点 , 处测出点的仰角度数,可以求出信号塔的高.如图,的长为 , 高为 . 他在点处测得点的仰角为 , 在点处测得点的仰角为 , 在同一平面内.你认为小王同学能求出信号塔的高吗?若能,请求出信号塔的高;若不能,请说明理由.(参考数据: , , , 结果保留整数)
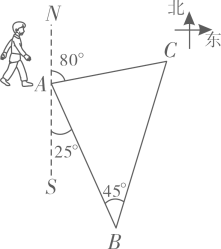
 17. 为了丰富学生的文化生活,学校利用假期组织学生到素质教育基地A和科技智能馆B参观学习,学生从学校出发,走到C处时,发现A位于C的北偏西方向上,B位于C的北偏西方向上,老师将学生分成甲乙两组,甲组前往A地,乙组前往B地,已知B在A的南偏西方向上,且相距1000米,请求出甲组同学比乙组同学大约多走多远的路程(参考数据: , )
17. 为了丰富学生的文化生活,学校利用假期组织学生到素质教育基地A和科技智能馆B参观学习,学生从学校出发,走到C处时,发现A位于C的北偏西方向上,B位于C的北偏西方向上,老师将学生分成甲乙两组,甲组前往A地,乙组前往B地,已知B在A的南偏西方向上,且相距1000米,请求出甲组同学比乙组同学大约多走多远的路程(参考数据: , ) 18. 为了增强学生体质、针炼学生意志,某校组织一次定向越野拉练活动.如图,A点为出发点,途中设置两个检查点,分别为点和点,行进路线为.点在点的南偏东方向处,点在点的北偏东方向,行进路线AB和BC所在直线的夹角为.
18. 为了增强学生体质、针炼学生意志,某校组织一次定向越野拉练活动.如图,A点为出发点,途中设置两个检查点,分别为点和点,行进路线为.点在点的南偏东方向处,点在点的北偏东方向,行进路线AB和BC所在直线的夹角为.⑴求行进路线BC和CA所在直线的夹角的度数;
⑵求检查点和之间的距离(结果保留根号).
 19. 贵州旅游资源丰富.某景区为给游客提供更好的游览体验,拟在如图①景区内修建观光索道.设计示意图如图②所示,以山脚为起点,沿途修建、两段长度相等的观光索道,最终到达山顶处,中途设计了一段与平行的观光平台为 . 索道与的夹角为 , 与水平线夹角为 , 两处的水平距离为 , , 垂足为点 . (图中所有点都在同一平面内,点在同一水平线上)
19. 贵州旅游资源丰富.某景区为给游客提供更好的游览体验,拟在如图①景区内修建观光索道.设计示意图如图②所示,以山脚为起点,沿途修建、两段长度相等的观光索道,最终到达山顶处,中途设计了一段与平行的观光平台为 . 索道与的夹角为 , 与水平线夹角为 , 两处的水平距离为 , , 垂足为点 . (图中所有点都在同一平面内,点在同一水平线上) (1)、求索道的长(结果精确到);(2)、求水平距离的长(结果精确到).
(1)、求索道的长(结果精确到);(2)、求水平距离的长(结果精确到).(参考数据: , , , )
20. “一缕清风银叶转”,某市20台风机依次矗立在云遮雾绕的山脊之上,风叶转动,风能就能转换成电能,造福千家万户.某中学初三数学兴趣小组,为测量风叶的长度进行了实地测量.如图,三片风叶两两所成的角为 , 当其中一片风叶与塔干叠合时,在与塔底D水平距离为60米的E处,测得塔顶部O的仰角 , 风叶的视角 .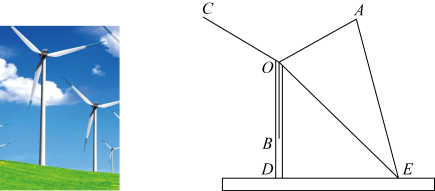 (1)、已知α,β两角和的余弦公式为: , 请利用公式计算;(2)、求风叶的长度.21. 阅读下列材料,回答问题
(1)、已知α,β两角和的余弦公式为: , 请利用公式计算;(2)、求风叶的长度.21. 阅读下列材料,回答问题任务:测量一个扁平状的小水池的最大宽度,该水池东西走向的最大度远大于南北走向的最大宽度,如图1.
工具:一把皮尺(测量长度略小于)和一台测角仪,如图2.皮尺的功能是直接测量任意可到达的两点间的距离(这两点间的距离不大于皮尺的测量长度);测角仪的功能是测量角的大小,即在任一点处,对其视线可及的两点,可测得的大小,如图3.

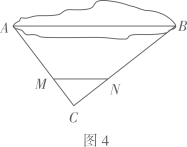
小明利用皮尺测量,求出了小水池的最大宽度 , 其测量及求解过程如下:测量过程:
(ⅰ)在小水池外选点 , 如图4,测得;
(ⅱ)分别在上测得;测得 . 求解过程:
由测量知, ,
, 又①____,
.
又②____( .
故小水池的最大宽度为____ .
(1)、补全小明求解过程中①②所缺的内容;(2)、小明求得用到的几何知识是;(3)、小明仅利用皮尺,通过5次测量,求得 . 请你同时利用皮尺和测角仪,通过测量长度、角度等几何量,并利用解直角三角形的知识求小水池的最大宽度 , 写出你的测量及求解过程.要求:测量得到的长度用字母表示,角度用表示;测量次数不超过4次(测量的几何量能求出 , 且测量的次数最少,才能得满分).
22. 【问题背景】由光的反射定律知:反射角等于入射角(如图,即).小军测量某建筑物高度的方法如下:在地面点E处平放一面镜子,经调整自己位置后,在点D处恰好通过镜子看到建筑物AB的顶端A . 经测得,小军的眼睛离地面的距离 , , , 求建筑物AB的高度.
【活动探究】
观察小军的操作后,小明提出了一个测量广告牌高度的做法(如图):他让小军站在点D处不动,将镜子移动至处,小军恰好通过镜子看到广告牌顶端G , 测出;再将镜子移动至处,恰好通过镜子看到广告牌的底端A , 测出 . 经测得,小军的眼睛离地面距离 , , 求这个广告牌AG的高度.

【应用拓展】
小军和小明讨论后,发现用此方法也可测量出斜坡上信号塔AB的高度.他们给出了如下测量步骤(如图):①让小军站在斜坡的底端D处不动(小军眼睛离地面距离),小明通过移动镜子(镜子平放在坡面上)位置至E处,让小军恰好能看到塔顶B;②测出;③测出坡长;④测出坡比为(即).通过他们给出的方案,请你算出信号塔AB的高度(结果保留整数).
