【培优卷】1.5三角函数的应用—北师大版数学九年级下册同步测试
试卷更新日期:2023-09-17 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 图中的梯形ABCD是水坝的一个截面图,阴影部分是外坡面土方的部分.其中 , , , , m,AD=5m,则坝底外坡面土方的水平宽度BE长为( )
 A、m B、m C、m D、m2. 如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.则斜坡CD的长度为( ).
A、m B、m C、m D、m2. 如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.则斜坡CD的长度为( ). A、 B、 C、 D、3. 数学兴趣小组利用无人机测量学校旗杆高度,已知无人机的飞行高度为37米,当无人机与旗杆的水平距离是45米时,观测旗杆顶部的俯角为 , 则旗杆的高度约为( )
A、 B、 C、 D、3. 数学兴趣小组利用无人机测量学校旗杆高度,已知无人机的飞行高度为37米,当无人机与旗杆的水平距离是45米时,观测旗杆顶部的俯角为 , 则旗杆的高度约为( ) A、米 B、 C、 D、22.5米4. 年月日,神舟十三号载人飞船返回舱在东风着陆场成功着陆,神舟十三号载人飞行任务收得圆满成功,中国航天,又站在了一个新的起点.如图年月日,神舟十三号载人飞船从地面处成功发射,当飞船到达点时,地面处的雷达站测得米,仰角为 , 秒后,飞船直线上升到达点处,此时地面处的雷达站测得处的仰角为.点 , , 在同一直线上,已知 , 两处相距米,则飞船从到处的平均速度为( )米秒.(结果精确到米;参考数据: , )
A、米 B、 C、 D、22.5米4. 年月日,神舟十三号载人飞船返回舱在东风着陆场成功着陆,神舟十三号载人飞行任务收得圆满成功,中国航天,又站在了一个新的起点.如图年月日,神舟十三号载人飞船从地面处成功发射,当飞船到达点时,地面处的雷达站测得米,仰角为 , 秒后,飞船直线上升到达点处,此时地面处的雷达站测得处的仰角为.点 , , 在同一直线上,已知 , 两处相距米,则飞船从到处的平均速度为( )米秒.(结果精确到米;参考数据: , ) A、336 B、335 C、334 D、3335. 如图,轮船在A处观测灯塔C位于北偏西方向上,轮船从A处以每小时40海里的速度沿南偏西方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西方向上,则下列说法正确的是( )
A、336 B、335 C、334 D、3335. 如图,轮船在A处观测灯塔C位于北偏西方向上,轮船从A处以每小时40海里的速度沿南偏西方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西方向上,则下列说法正确的是( ) A、 B、点B到的距离为海里 C、海里 D、点B在点C的南偏东的方向上6. 最近央视纪录片《航拍中国》中各地的美景震撼了全国观众,如图是航拍无人机从A点俯拍在坡比为3:4的斜坡CD上的景点C,此时的俯角为30°,为取得更震撼的拍摄效果,无人机升高200米到达B点,此时的俯角变为45°.已知无人机与斜坡CD的坡底D的水平距离DE为400米,则斜坡CD的长度为( )米(精确到0.1米,参考数据:≈1.41,≈1.73)
A、 B、点B到的距离为海里 C、海里 D、点B在点C的南偏东的方向上6. 最近央视纪录片《航拍中国》中各地的美景震撼了全国观众,如图是航拍无人机从A点俯拍在坡比为3:4的斜坡CD上的景点C,此时的俯角为30°,为取得更震撼的拍摄效果,无人机升高200米到达B点,此时的俯角变为45°.已知无人机与斜坡CD的坡底D的水平距离DE为400米,则斜坡CD的长度为( )米(精确到0.1米,参考数据:≈1.41,≈1.73) A、91.1 B、91.3 C、58.2 D、58.47. 如图,中, , , 于点 , 若点是线段上一动点,则的最小值为( )
A、91.1 B、91.3 C、58.2 D、58.47. 如图,中, , , 于点 , 若点是线段上一动点,则的最小值为( ) A、 B、 C、 D、8. 如图,在观测站O处测得船A和灯塔B分别位于正东方向和北偏东60°方向,灯塔B位于船A的北偏东15°方向4海里处,若船A向正东航行,则船A离灯塔B的最近距离是( )
A、 B、 C、 D、8. 如图,在观测站O处测得船A和灯塔B分别位于正东方向和北偏东60°方向,灯塔B位于船A的北偏东15°方向4海里处,若船A向正东航行,则船A离灯塔B的最近距离是( )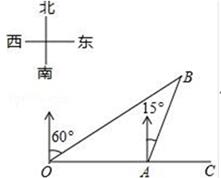 A、( + )海里 B、2 海里 C、( +1)海里 D、2 海里9. 一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是( )(结果保留小数点后两位)(参考数据: )A、4.64海里 B、5.49海里 C、6.12海里 D、6.21海里10. 一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1 , E1 , E2 , C2 , E3 , E4 , C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2018B2018C2018D2018的边长是( )
A、( + )海里 B、2 海里 C、( +1)海里 D、2 海里9. 一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是( )(结果保留小数点后两位)(参考数据: )A、4.64海里 B、5.49海里 C、6.12海里 D、6.21海里10. 一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1 , E1 , E2 , C2 , E3 , E4 , C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2018B2018C2018D2018的边长是( )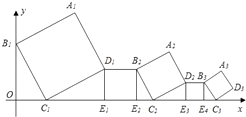 A、( )2017 B、( )2016 C、( )2017 D、( )2016
A、( )2017 B、( )2016 C、( )2017 D、( )2016二、填空题(每题3分,共15分)
-
11. 图1所示是一种单臂篮球架,其侧面示意图如图2所示,其中支架AB垂直于地面BE , 支架AC与AB的夹角为115°,篮筐DP与支架PC都平行于地面BE . 现已知AB=2.50米,CA=1.30米,则篮筐DP距离地面的高度为米.(精确到0.01米.参考数据:sin25°≈0.42,cos25°≈0.91,tan25°≈0.47)

 12. 图1是某折叠式靠背椅实物图,图2是椅子打开时的侧面示意图,椅面CE与地面平行,支撑杆AD,BC可绕连接点O转动,且 , 椅面底部有一根可以绕点H转动的连杆HD,点H是CD的中点,FA,EB均与地面垂直,测得FA=54cm,EB=45cm,AB=48cm.
12. 图1是某折叠式靠背椅实物图,图2是椅子打开时的侧面示意图,椅面CE与地面平行,支撑杆AD,BC可绕连接点O转动,且 , 椅面底部有一根可以绕点H转动的连杆HD,点H是CD的中点,FA,EB均与地面垂直,测得FA=54cm,EB=45cm,AB=48cm. (1)、椅面CE的长度为cm.(2)、如图3,椅子折叠时,连杆HD绕着支点H带动支撑杆AD,BC转动合拢,椅面和连杆夹角∠CHD的度数达到最小值30°时,A,B两点间的距离为cm(结果精确到0.1cm).13. 疫情期间,小红在家里在图1所示的平板支架上网课,图2是她观看网课的侧面示意图,已知平板宽度AB=20cm,支架底板宽度CD=AB,支撑角∠ABC=60°,支撑板CE=BE=6cm,小红坐在距离支架底板20cm处观看(即DF=20cm),Q点是AB中点.当视线PQ与屏幕AB垂直时,小红的眼睛距离桌面的高度PF等于 cm;当落在屏幕中点的视线与屏幕构成的夹角(指锐角或直角)不小于75°时,能使观看平板视频的效果最佳,为保证最佳的观看效果,小红眼睛距离桌面的最大高度和最小高度的差等于 cm.
(1)、椅面CE的长度为cm.(2)、如图3,椅子折叠时,连杆HD绕着支点H带动支撑杆AD,BC转动合拢,椅面和连杆夹角∠CHD的度数达到最小值30°时,A,B两点间的距离为cm(结果精确到0.1cm).13. 疫情期间,小红在家里在图1所示的平板支架上网课,图2是她观看网课的侧面示意图,已知平板宽度AB=20cm,支架底板宽度CD=AB,支撑角∠ABC=60°,支撑板CE=BE=6cm,小红坐在距离支架底板20cm处观看(即DF=20cm),Q点是AB中点.当视线PQ与屏幕AB垂直时,小红的眼睛距离桌面的高度PF等于 cm;当落在屏幕中点的视线与屏幕构成的夹角(指锐角或直角)不小于75°时,能使观看平板视频的效果最佳,为保证最佳的观看效果,小红眼睛距离桌面的最大高度和最小高度的差等于 cm.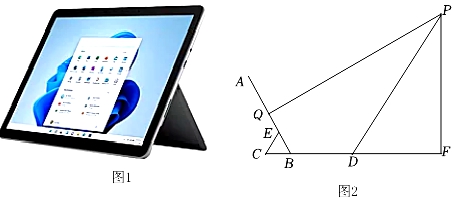 14. 足球射门时,在不考虑其他因素的条件下,射点到球门AB的张角越大,射门越好. 当张角达到最大值时,我们称该射点为最佳射门点. 通过研究发现,如图1所示,一学生带球在直线CD上行进时,当存在一点Q,使得∠CQA=∠ABQ(此时也有∠DQB=∠QAB)时,恰好能使球门AB的张角∠AQB达到最大值,故可以称点Q为直线CD上的最佳射门点.如图2所示,是一个矩形形状的足球场,AB为球门一部分,CD⊥AB于点D,AB=6米,BD=2米.某球员沿CD向球门AB进攻,设最佳射门点为点Q.
14. 足球射门时,在不考虑其他因素的条件下,射点到球门AB的张角越大,射门越好. 当张角达到最大值时,我们称该射点为最佳射门点. 通过研究发现,如图1所示,一学生带球在直线CD上行进时,当存在一点Q,使得∠CQA=∠ABQ(此时也有∠DQB=∠QAB)时,恰好能使球门AB的张角∠AQB达到最大值,故可以称点Q为直线CD上的最佳射门点.如图2所示,是一个矩形形状的足球场,AB为球门一部分,CD⊥AB于点D,AB=6米,BD=2米.某球员沿CD向球门AB进攻,设最佳射门点为点Q.
 (1)、tan∠AQB= .(2)、已知对方守门员伸开双臂后,成功防守的范围为 ,若此时守门员站在张 角∠AQB内,双臂张开MN垂直于AQ进行防守,为了确保防守成功,MN中点与AB的距离至少为 .15. 随着“科学运动、健康生活”的理念深入人心,跑步机已成为家居新宠,某品牌跑步机(如图1)的跑道可以旋转(如图2),图3为跑道 绕 点旋转到 位置时的主视图,其中 为显示屏, 为扶手,点 在直线 上, 为可伸缩液压支撑杆, 的位置不变, 的长度可变化,已知 ,则 .若 ,且 恰好在同一直线上,则 .
(1)、tan∠AQB= .(2)、已知对方守门员伸开双臂后,成功防守的范围为 ,若此时守门员站在张 角∠AQB内,双臂张开MN垂直于AQ进行防守,为了确保防守成功,MN中点与AB的距离至少为 .15. 随着“科学运动、健康生活”的理念深入人心,跑步机已成为家居新宠,某品牌跑步机(如图1)的跑道可以旋转(如图2),图3为跑道 绕 点旋转到 位置时的主视图,其中 为显示屏, 为扶手,点 在直线 上, 为可伸缩液压支撑杆, 的位置不变, 的长度可变化,已知 ,则 .若 ,且 恰好在同一直线上,则 .
三、解答题(共7题,共55分)
-
16. 如图,某数学兴趣小组为了测量古树的高度,采用了如下的方法:先从与古树底端在同一水平线上的点A出发,沿斜面坡度为的斜坡前进到达点 , 再沿水平方向继续前进一段距离后到达点 . 在点处测得古树的顶端的俯角为 , 底部的俯角为 , 求古树的高度(参考数据: , , , 计算结果用根号表示,不取近似值).
 17. 2022年底,太忻一体化经济区将新建1994座5G基站.如图是建在坡度的斜坡上的一个5G基站塔 , 在坡角顶点A处测得塔顶D的仰角为 , 沿斜坡步行到达B处,在B处测得塔顶D的仰角为 , 点A,B,C,D,M,N在同一平面内.求基站塔高 .
17. 2022年底,太忻一体化经济区将新建1994座5G基站.如图是建在坡度的斜坡上的一个5G基站塔 , 在坡角顶点A处测得塔顶D的仰角为 , 沿斜坡步行到达B处,在B处测得塔顶D的仰角为 , 点A,B,C,D,M,N在同一平面内.求基站塔高 .(结果精确到 , 参考数据:)
 18. 如图是一个小商场的纵截面图(矩形 ), 是商场的顶部, 是商场的地面,地面由边长为 的正方形瓷砖铺成,从 到 共有 块瓷砖, 和 是商场的两面墙壁, 是顶部正中央的一个长方形的灯饰( ).小张同学想通过学过的几何知识来测量该商场的高度( )和灯饰的长度( ),于是去商场时带了一块镜子和一根激光笔,他先把激光笔挂在墙壁 距地面两块砖高度( 的长)的 处,镜子水平放在地面距离 两块砖的 处,发现激光笔的反射光照到了 处;再把激光笔挂在墙壁 距地面两块砖高度( 的长)的 处,镜子水平放在地面距离 三块砖的 处,发现激光笔的反射光恰好又照到了 处,请你帮忙计算 的高度和 的长度.
18. 如图是一个小商场的纵截面图(矩形 ), 是商场的顶部, 是商场的地面,地面由边长为 的正方形瓷砖铺成,从 到 共有 块瓷砖, 和 是商场的两面墙壁, 是顶部正中央的一个长方形的灯饰( ).小张同学想通过学过的几何知识来测量该商场的高度( )和灯饰的长度( ),于是去商场时带了一块镜子和一根激光笔,他先把激光笔挂在墙壁 距地面两块砖高度( 的长)的 处,镜子水平放在地面距离 两块砖的 处,发现激光笔的反射光照到了 处;再把激光笔挂在墙壁 距地面两块砖高度( 的长)的 处,镜子水平放在地面距离 三块砖的 处,发现激光笔的反射光恰好又照到了 处,请你帮忙计算 的高度和 的长度. 19. 如图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图.量得托板长AB=130mm,支撑板长CD=80mm,底座长DE=90mm.托板AB固定在支撑板顶端点C处,且CB=40mm,托板AB可绕点C转动,支撑板CD可绕点D转动.(结果保留小数点后一位)
19. 如图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图.量得托板长AB=130mm,支撑板长CD=80mm,底座长DE=90mm.托板AB固定在支撑板顶端点C处,且CB=40mm,托板AB可绕点C转动,支撑板CD可绕点D转动.(结果保留小数点后一位) (1)、若∠DCB=80°,∠CDE=60°,求点A到直线DE的距离;(2)、为了观看舒适,在(1)的情况下,把AB绕点C逆时针旋转10°后,再将CD绕点D顺时针旋转,使点B落在直线DE上即可,求CD旋转的角度.(参考数据:sin40°≈0.643,cos40°≈0.766,tan40°≈0.839,sin26.6°≈0.448,cos26.6°≈0.894,tan26.6°≈0.500, ≈1.732)20. 随着科技的发展,无人机已广泛应用于生产生活,如代替人们在高空测量距离和高度.圆圆要测量教学楼的高度,借助无人机设计了如下测量方案:如图,圆圆在离教学楼底部米的C处,遥控无人机旋停在点C的正上方的点D处,测得教学楼的顶部B处的俯角为 , 长为米.已知目高为米.
(1)、若∠DCB=80°,∠CDE=60°,求点A到直线DE的距离;(2)、为了观看舒适,在(1)的情况下,把AB绕点C逆时针旋转10°后,再将CD绕点D顺时针旋转,使点B落在直线DE上即可,求CD旋转的角度.(参考数据:sin40°≈0.643,cos40°≈0.766,tan40°≈0.839,sin26.6°≈0.448,cos26.6°≈0.894,tan26.6°≈0.500, ≈1.732)20. 随着科技的发展,无人机已广泛应用于生产生活,如代替人们在高空测量距离和高度.圆圆要测量教学楼的高度,借助无人机设计了如下测量方案:如图,圆圆在离教学楼底部米的C处,遥控无人机旋停在点C的正上方的点D处,测得教学楼的顶部B处的俯角为 , 长为米.已知目高为米. (1)、求教学楼的高度.(2)、若无人机保持现有高度沿平行于的方向,以米/秒的速度继续向前匀速飞行,求经过多少秒时,无人机刚好离开圆圆的视线 .21. 小明家住在某小区一楼,购房时开发商赠送了一个露天活动场所,现小明在活动场所正对的墙上安装了一个遮阳棚 , 经测量,安装遮阳棚的那面墙高 , 安装的遮阳棚展开后可以使正午时刻房前能有宽的阴影处以供纳凉.已知正午时刻太阳光与水平地面的夹角为 , 安装好的遮阳篷与水平面的夹角为 , 如下右图为侧面示意图.
(1)、求教学楼的高度.(2)、若无人机保持现有高度沿平行于的方向,以米/秒的速度继续向前匀速飞行,求经过多少秒时,无人机刚好离开圆圆的视线 .21. 小明家住在某小区一楼,购房时开发商赠送了一个露天活动场所,现小明在活动场所正对的墙上安装了一个遮阳棚 , 经测量,安装遮阳棚的那面墙高 , 安装的遮阳棚展开后可以使正午时刻房前能有宽的阴影处以供纳凉.已知正午时刻太阳光与水平地面的夹角为 , 安装好的遮阳篷与水平面的夹角为 , 如下右图为侧面示意图.

(参考数据: , , , , , )
(1)、据研究,当一个人从遮阳棚进出时,如果遮阳棚外端(即图中点C)到地面的距离小于时,则人进出时总会觉得没有安全感,就会不自觉的低下头或者用手护着头,请你通过计算,判断此遮阳棚是否使得人进出时具有安全感?(2)、请计算此遮阳棚延展后的长度(即的长度).(结果精确到)22. 太极揉推器是一种常见的公共健身器械,如图是某太极揉推器的实物图和侧面示意图.立柱高1.2m,底面直径为10cm,支架和长均为50cm,且均与立柱所夹锐角为45°,支点A,C到立柱顶端的垂直距离均为40cm,转盘的直径和长均为48cm,且分别与和垂直,点B,D分别是 , 的中点. (1)、该太极揉推器的直径和所在直线的夹角为;(2)、求该太极揉推器的高度h(即点E到地面的距离);(3)、请直接判断该太极揉推器的高度h与宽度w(即线段在地面的正投影长)的大小关系:hw.
(1)、该太极揉推器的直径和所在直线的夹角为;(2)、求该太极揉推器的高度h(即点E到地面的距离);(3)、请直接判断该太极揉推器的高度h与宽度w(即线段在地面的正投影长)的大小关系:hw.