【提升卷】1.4解直角三角形—北师大版数学九年级下册同步测试
试卷更新日期:2023-09-17 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图是一个以O为对称中心的中心对称图形,若∠A=30°,∠C=90°,AC=1,则AB的长为( )
 A、4 B、 C、 D、2. 已知直线 , 且相邻的两条平行直线间的距离均等,将一个含45°的直角三角板按图示放置,使其三个顶点分别在三条平行线上,则的值是( )
A、4 B、 C、 D、2. 已知直线 , 且相邻的两条平行直线间的距离均等,将一个含45°的直角三角板按图示放置,使其三个顶点分别在三条平行线上,则的值是( ) A、 B、 C、 D、3. 将矩形纸片ABCD按如图所示的方式折叠.恰好得到菱形AECF.若AD= , 则菱形AECF的面积为( )
A、 B、 C、 D、3. 将矩形纸片ABCD按如图所示的方式折叠.恰好得到菱形AECF.若AD= , 则菱形AECF的面积为( ) A、2 B、4 C、4 D、84. 如图所示,是由小正方形构成的网格,每个小正方形的顶点叫做格点,点 , , , , 均在格点上,则和的大小关系为( )
A、2 B、4 C、4 D、84. 如图所示,是由小正方形构成的网格,每个小正方形的顶点叫做格点,点 , , , , 均在格点上,则和的大小关系为( ) A、 B、 C、 D、无法确定5. 如图,一块矩形薄木板斜靠在墙角处( , 点 , , , , , , 在同一平面内),已知 , , , 则点到的距离等于( )
A、 B、 C、 D、无法确定5. 如图,一块矩形薄木板斜靠在墙角处( , 点 , , , , , , 在同一平面内),已知 , , , 则点到的距离等于( ) A、 B、 C、 D、6. 如图,直线MN是矩形ABCD的一条对称轴,点E在AD边E上,将沿BE折叠,使点A的对应点F落在直线MN上,若 , 则BE的长是( )
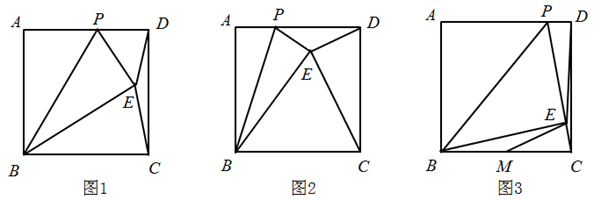
A、 B、 C、 D、6. 如图,直线MN是矩形ABCD的一条对称轴,点E在AD边E上,将沿BE折叠,使点A的对应点F落在直线MN上,若 , 则BE的长是( )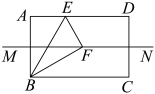 A、5 B、 C、 D、7. 如图,将长、宽分别为6cm, cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)面积为( )
A、5 B、 C、 D、7. 如图,将长、宽分别为6cm, cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)面积为( )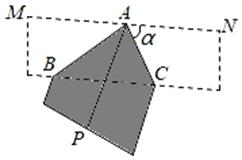 A、 cm2 B、(36 )cm2 C、 cm2 D、 cm28. 如图,在△ABC中,∠C=45°,= , AD⊥BC于点D,AC= , 若E、F分别为AC、BC的中点,则EF的长为( )
A、 cm2 B、(36 )cm2 C、 cm2 D、 cm28. 如图,在△ABC中,∠C=45°,= , AD⊥BC于点D,AC= , 若E、F分别为AC、BC的中点,则EF的长为( ) A、 B、2 C、 D、9. 如图,在平面直角坐标系中,直线AB与x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线(k≠0)上,则k的值为( )
A、 B、2 C、 D、9. 如图,在平面直角坐标系中,直线AB与x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线(k≠0)上,则k的值为( )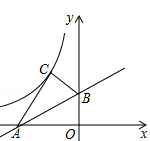 A、4 B、﹣2 C、 D、10. 由12个有公共顶点O的直角三角形拼成如图所示的图形, , . 若 , 则图中与位似的三角形的面积为( )
A、4 B、﹣2 C、 D、10. 由12个有公共顶点O的直角三角形拼成如图所示的图形, , . 若 , 则图中与位似的三角形的面积为( )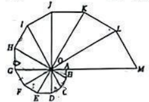 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共15分)
-
11. 已知在中,于D, , , , 则线段AB的长为 .12. 如图,四边形中, , 平分 , 交于点 , , 那么 .
 13. 如图,在△ABC中,∠ACB=90°,点D在AB边上,AD=AC,点E在BC边上,∠BAE=∠ABC,点F为AE上一点,∠ADF=2∠BCD,若DF=2,BD=1,则AD的长为 .
13. 如图,在△ABC中,∠ACB=90°,点D在AB边上,AD=AC,点E在BC边上,∠BAE=∠ABC,点F为AE上一点,∠ADF=2∠BCD,若DF=2,BD=1,则AD的长为 .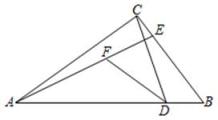 14. 如图,将一个边长为10cm的正方形活动据架(边框粗细忽略不计)拉动成四边形ABCD,若∠BAD=60°,则AC=cm.
14. 如图,将一个边长为10cm的正方形活动据架(边框粗细忽略不计)拉动成四边形ABCD,若∠BAD=60°,则AC=cm. 15. 如图,点F,G分别在正方形ABCD的边BC,CD上,E为AB中点,连结ED,正方形FGQP的边PQ恰好在DE上,记正方形ABCD面积为 , 正方形FPQG面积为 , 则的值为 .
15. 如图,点F,G分别在正方形ABCD的边BC,CD上,E为AB中点,连结ED,正方形FGQP的边PQ恰好在DE上,记正方形ABCD面积为 , 正方形FPQG面积为 , 则的值为 .
三、解答题(共7题,共55分)
-
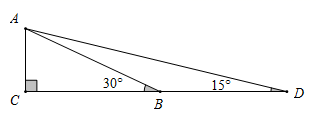
16. 构建几何图形解决代数问题是“数形结合”思想的重要策略.在计算 时,如图,在 中, ,延长 使 ,连接 ,得 ,所以 ,类比这种方法,计算 (画图并写出过程)
 17. 定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点与该边所对顶点所连线段长度的平方,则称这个点为三角形该边的“奇点”.如图①,在中,点D是边上一点,连接 , 若 , 则称点D是中边上的“奇点”.问题解决:如图②,在中, , , , 点D是边上的“奇点”,求线段的长.
17. 定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点与该边所对顶点所连线段长度的平方,则称这个点为三角形该边的“奇点”.如图①,在中,点D是边上一点,连接 , 若 , 则称点D是中边上的“奇点”.问题解决:如图②,在中, , , , 点D是边上的“奇点”,求线段的长. 18. 如图,是菱形的对角线.(1)、尺规作图:将绕点逆时针旋转得到 , 点旋转后的对应点为保留作图痕迹,不写作法;(2)、在(1)所作的图中,连接 , .
18. 如图,是菱形的对角线.(1)、尺规作图:将绕点逆时针旋转得到 , 点旋转后的对应点为保留作图痕迹,不写作法;(2)、在(1)所作的图中,连接 , .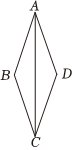
求证:∽;
若 , 求的值.
19. 如图,在Rt△ABC中, , D为AB的中点, , .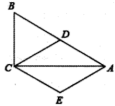 (1)、证明:四边形ADCE为菱形;(2)、若 , , 求四边形ADCE的周长.
(1)、证明:四边形ADCE为菱形;(2)、若 , , 求四边形ADCE的周长.