【培优卷】1.4解直角三角形—北师大版数学九年级下册同步测试
试卷更新日期:2023-09-17 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,在边长为4的正方形ABCD中,点E是CD边上的一点,点F是点D关于直线AE对称的点,连接AF、BF,若tan∠ABF=2,则DE的长是( )
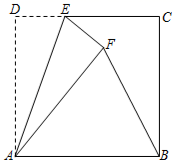 A、1 B、 C、 D、2. 如图,已知反比例函数 (k≠0)的图象经过矩形ABCD的对角线AC的端点A和C,AC交y轴于点F,BC边交y轴于点E,过线段FO中点G的直线与AC平行,连接AE,若∠BAE=∠ACB, . 则k的值为( )
A、1 B、 C、 D、2. 如图,已知反比例函数 (k≠0)的图象经过矩形ABCD的对角线AC的端点A和C,AC交y轴于点F,BC边交y轴于点E,过线段FO中点G的直线与AC平行,连接AE,若∠BAE=∠ACB, . 则k的值为( )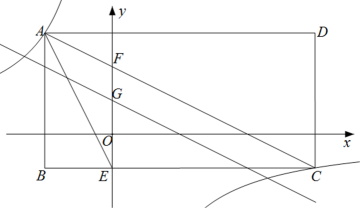 A、-24 B、-16 C、-36 D、-123. 如图①,在菱形 中, ,点 是 的中点,点 是对角线 上一动点,设 , ,图②是 关于 的函数图象,且图象上最低点 的坐标为 ,则菱形 的边长为( )
A、-24 B、-16 C、-36 D、-123. 如图①,在菱形 中, ,点 是 的中点,点 是对角线 上一动点,设 , ,图②是 关于 的函数图象,且图象上最低点 的坐标为 ,则菱形 的边长为( ) A、2 B、 C、 D、44. 如图,以矩形 的顶点 为圆心,适当长为半径作弧,分别交 , 于点 , ;再分别以点 , 为圆心,大于 的长为半径作弧,两弧交于点 ;作射线 ,交 于点 ,连接 ,交 于点 .若 , ,则 的长为( )
A、2 B、 C、 D、44. 如图,以矩形 的顶点 为圆心,适当长为半径作弧,分别交 , 于点 , ;再分别以点 , 为圆心,大于 的长为半径作弧,两弧交于点 ;作射线 ,交 于点 ,连接 ,交 于点 .若 , ,则 的长为( )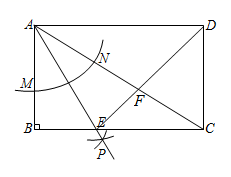 A、1 B、 C、 D、5. 在平面直角坐标系中,平行四边形ABCD的顶点A在y轴上,点C坐标为(﹣4,0),E为BC上靠近点C的三等分点,点B、E均在反比例函数y= (k<0,x<0)的图象上,若tan∠OAD= ,则k的值为( )
A、1 B、 C、 D、5. 在平面直角坐标系中,平行四边形ABCD的顶点A在y轴上,点C坐标为(﹣4,0),E为BC上靠近点C的三等分点,点B、E均在反比例函数y= (k<0,x<0)的图象上,若tan∠OAD= ,则k的值为( )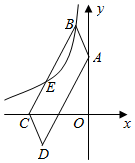 A、﹣2 B、﹣2 C、﹣6 D、﹣46. 如图,在平面直角坐标系 中, , , , 是正方形 边上的线段,点 在其中某条线段上,若射线 与 轴正半轴的夹角为 ,且 ,则点 所在的线段可以是
A、﹣2 B、﹣2 C、﹣6 D、﹣46. 如图,在平面直角坐标系 中, , , , 是正方形 边上的线段,点 在其中某条线段上,若射线 与 轴正半轴的夹角为 ,且 ,则点 所在的线段可以是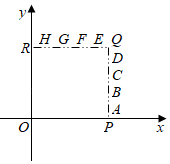 A、 和 B、 和 C、 和 D、 和7. 已知如图, 中, , ,D为线段 上一点,将线段 绕点A逆时针旋转 得到线段 ,F为 中点,直线 交射线 于点G.下列说法:①若连接 ,则 ;② ;③ ;④若 ,则 .其中正确的有( )
A、 和 B、 和 C、 和 D、 和7. 已知如图, 中, , ,D为线段 上一点,将线段 绕点A逆时针旋转 得到线段 ,F为 中点,直线 交射线 于点G.下列说法:①若连接 ,则 ;② ;③ ;④若 ,则 .其中正确的有( ) A、1个 B、2个 C、3个 D、4个8. 如图,已知点A是第一象限内横坐标为2 的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动,求当点P从点O运动到点N时,点B运动的路径长为( ).
A、1个 B、2个 C、3个 D、4个8. 如图,已知点A是第一象限内横坐标为2 的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动,求当点P从点O运动到点N时,点B运动的路径长为( ). A、 B、 C、4 D、9. 如图,在 中, , , 于点D , 于点E , .连接DE , 将 沿直线AE翻折至 所在的平面内,得 ,连接DF . 过点D作 交BE于点G . 则四边形DFEG的周长为( )
A、 B、 C、4 D、9. 如图,在 中, , , 于点D , 于点E , .连接DE , 将 沿直线AE翻折至 所在的平面内,得 ,连接DF . 过点D作 交BE于点G . 则四边形DFEG的周长为( )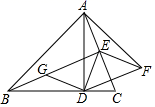 A、8 B、 C、 D、10. 如果,正方形ABCD的边长为2cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q,若PQ=AE,则PD等于( )
A、8 B、 C、 D、10. 如果,正方形ABCD的边长为2cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q,若PQ=AE,则PD等于( )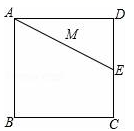 A、 cm或 cm B、 cm C、 cm或 cm D、 cm或 cm
A、 cm或 cm B、 cm C、 cm或 cm D、 cm或 cm二、填空题(每题3分,共15分)
-
11. 如图.四边形中, , , , 交于点 , , , 则AB的长为 .
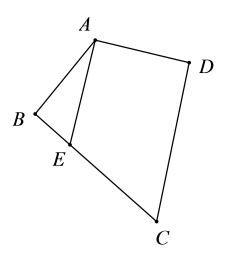 12. 如图,将平行四边形沿着对角线翻折,点的对应点为 , 交于点 , 如果 , , 且 , 那么平行四边形的周长为 .(参考数据:)
12. 如图,将平行四边形沿着对角线翻折,点的对应点为 , 交于点 , 如果 , , 且 , 那么平行四边形的周长为 .(参考数据:) 13. 如图,矩形的顶点在反比例函数的图像上,顶点在第一象限,对角线轴,交轴于点.若矩形的面积是 , 则.
13. 如图,矩形的顶点在反比例函数的图像上,顶点在第一象限,对角线轴,交轴于点.若矩形的面积是 , 则. 14. 如图,直线与x轴,y轴分别交于A,B两点,点D是线段AB上一动点,点H是直线上的一动点,动点 , 连接 . 当取最小值时,的最小值是 .
14. 如图,直线与x轴,y轴分别交于A,B两点,点D是线段AB上一动点,点H是直线上的一动点,动点 , 连接 . 当取最小值时,的最小值是 .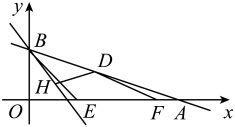 15. 如图1,将一张等腰三角形纸片沿虚线剪开,得到两个全等的三角形和两个全等的四边形小纸片.小博按图2方式拼接,恰好拼成一个不重叠、无缝隙的矩形;小雅按图3方式拼接,也拼出一个矩形 , 但由于两个四边形纸片有重叠(阴影)部分,整个面积减少了.若 , 则 , 矩形的面积为 .
15. 如图1,将一张等腰三角形纸片沿虚线剪开,得到两个全等的三角形和两个全等的四边形小纸片.小博按图2方式拼接,恰好拼成一个不重叠、无缝隙的矩形;小雅按图3方式拼接,也拼出一个矩形 , 但由于两个四边形纸片有重叠(阴影)部分,整个面积减少了.若 , 则 , 矩形的面积为 .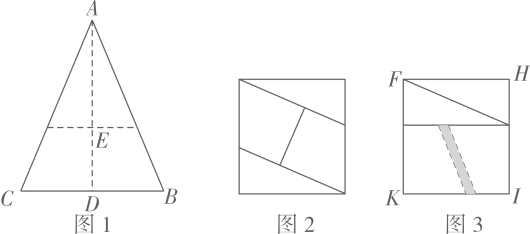
三、解答题(共7题,共55分)
-
16. 已知等边 , 其中点D、E是过顶点B的一条直线l上两点
 (1)、如图1, , 求证:(2)、如图2, , , , 求AD的长.17. 是等边三角形,点是射线上的一点(不与点 , 重合),连接 , 在的左侧作等边三角形 , 将线段绕点逆时针旋转 , 得到线段 , 连接 . 交于点 .
(1)、如图1, , 求证:(2)、如图2, , , , 求AD的长.17. 是等边三角形,点是射线上的一点(不与点 , 重合),连接 , 在的左侧作等边三角形 , 将线段绕点逆时针旋转 , 得到线段 , 连接 . 交于点 . (1)、如图1,当点为中点时,请直接写出线段与的数量关系;(2)、如图2.当点在线段的延长线上时,请判断()中的结论是否成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、当 , 时,请直接写出的长.18. 问题情境:“综合与实践”课上,老师提出如下问题:将图1中的矩形纸片沿对角线剪开,得到两个全等的三角形纸片,表示为和 , 其中 . 将和按图2所示方式摆放,其中点与点重合(标记为点).当时,延长交于点 . 试判断四边形的形状,并说明理由.
(1)、如图1,当点为中点时,请直接写出线段与的数量关系;(2)、如图2.当点在线段的延长线上时,请判断()中的结论是否成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、当 , 时,请直接写出的长.18. 问题情境:“综合与实践”课上,老师提出如下问题:将图1中的矩形纸片沿对角线剪开,得到两个全等的三角形纸片,表示为和 , 其中 . 将和按图2所示方式摆放,其中点与点重合(标记为点).当时,延长交于点 . 试判断四边形的形状,并说明理由.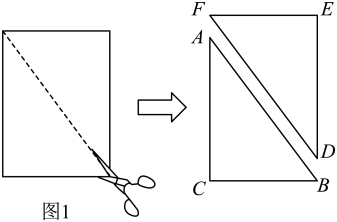 (1)、数学思考:谈你解答老师提出的问题;(2)、深入探究:老师将图2中的绕点逆时针方向旋转,使点落在内部,并让同学们提出新的问题.
(1)、数学思考:谈你解答老师提出的问题;(2)、深入探究:老师将图2中的绕点逆时针方向旋转,使点落在内部,并让同学们提出新的问题.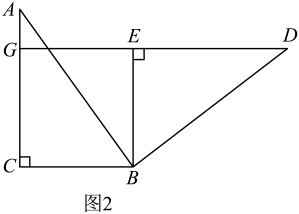
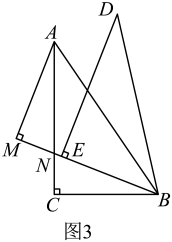
①“善思小组”提出问题:如图3,当时,过点作交的延长线于点与交于点 . 试猜想线段和的数量关系,并加以证明.请你解答此问题;
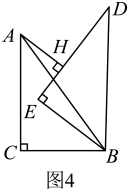
②“智慧小组”提出问题:如图4,当时,过点作于点 , 若 , 求的长.请你思考此问题,直接写出结果.
 19. 如图,在正方形中,E,F分别是边 , 上的点,连接 , , .
19. 如图,在正方形中,E,F分别是边 , 上的点,连接 , , . (1)、若正方形的边长为2,E是的中点.
(1)、若正方形的边长为2,E是的中点.①如图1,当时,求证:;
②如图2,当时,求的长;
(2)、如图3,延长 , 交于点G,当时,求证: .20. 在平面直角坐标系中,O为原点,菱形的顶点 , 矩形的顶点 .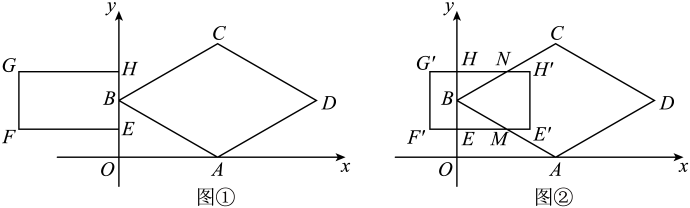 (1)、填空:如图①,点C的坐标为 , 点G的坐标为;(2)、将矩形沿水平方向向右平移,得到矩形 , 点E,F,G,H的对应点分别为 , , , . 设 , 矩形与菱形重叠部分的面积为S.
(1)、填空:如图①,点C的坐标为 , 点G的坐标为;(2)、将矩形沿水平方向向右平移,得到矩形 , 点E,F,G,H的对应点分别为 , , , . 设 , 矩形与菱形重叠部分的面积为S.①如图②,当边与相交于点M、边与相交于点N,且矩形与菱形重叠部分为五边形时,试用含有t的式子表示S,并直接写出t的取值范围:
②当时,求S的取值范围(直接写出结果即可).
21. 我们把两个面积相等但不全等的三角形叫关联三角形. (1)、如图1,已知等腰直角△ABC,∠ACB=90°,请将它分成两个三角形,使它们成为关联三角形.(2)、如图2,已知△ABC为直角三角形,∠ACB=90°,以AB,AC,BC为边向外作正方形ABDE,正方形ACFG和正方形BCMN,连结EG.求证:△ABC与△AEG为关联三角形.(3)、在△ABC中,∠A=30°,AC=8,点D在线段AC上,连接BD,△ABD和△BCD是关联三角形,将△ABD沿BD所在的直线翻折,得到△A1BD,若△A1BD与△BCD重合部分的面积等于△BCD面积的一半,求△ABC的面积.22. 【课本再现】黄金分割是一种最能引起美感的分割比例,具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值.我们知道:如图1,如果 , 那么称点为线段的黄金分割点.
(1)、如图1,已知等腰直角△ABC,∠ACB=90°,请将它分成两个三角形,使它们成为关联三角形.(2)、如图2,已知△ABC为直角三角形,∠ACB=90°,以AB,AC,BC为边向外作正方形ABDE,正方形ACFG和正方形BCMN,连结EG.求证:△ABC与△AEG为关联三角形.(3)、在△ABC中,∠A=30°,AC=8,点D在线段AC上,连接BD,△ABD和△BCD是关联三角形,将△ABD沿BD所在的直线翻折,得到△A1BD,若△A1BD与△BCD重合部分的面积等于△BCD面积的一半,求△ABC的面积.22. 【课本再现】黄金分割是一种最能引起美感的分割比例,具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值.我们知道:如图1,如果 , 那么称点为线段的黄金分割点. (1)、【问题发现】如图1,请直接写出与的比值是;(2)、【尺规作黄金分割点】如图2,在中, , , , 则 , 在上截取 , 则 , 在上截取 , 则的值为;(3)、【问题解决】如图3,用边长为4的正方形纸片进行如下操作:对折正方形得折痕 , 连接 , 点对应点 , 得折痕 , 试说明:是的黄金分割点;(4)、【拓展延伸】如图4,正方形中,为对角线上一点,点在边上,且 , 当为的黄金分割点时, , 连 , 延长交于 , 请用相似的知识求出的值为 .
(1)、【问题发现】如图1,请直接写出与的比值是;(2)、【尺规作黄金分割点】如图2,在中, , , , 则 , 在上截取 , 则 , 在上截取 , 则的值为;(3)、【问题解决】如图3,用边长为4的正方形纸片进行如下操作:对折正方形得折痕 , 连接 , 点对应点 , 得折痕 , 试说明:是的黄金分割点;(4)、【拓展延伸】如图4,正方形中,为对角线上一点,点在边上,且 , 当为的黄金分割点时, , 连 , 延长交于 , 请用相似的知识求出的值为 .