【基础卷】1.4解直角三角形—北师大版数学九年级下册同步测试
试卷更新日期:2023-09-17 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 在Rt△ABC中,∠C=90° , BC=6,sinA= , 则AB=( )A、8 B、9 C、10 D、122. 如图,在 Rt△ABC 中,∠C=90°,∠B=30°,AB=8,则 BC 的长是( )
 A、 B、4 C、8 D、43. 如图,在中, , , 那么下列结论正确的是( )
A、 B、4 C、8 D、43. 如图,在中, , , 那么下列结论正确的是( ) A、 B、 C、 D、4. 如图是的高, , , , 则的长为( ).
A、 B、 C、 D、4. 如图是的高, , , , 则的长为( ).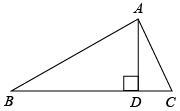 A、 B、 C、 D、5. 如图,是电杆的一根拉线,测得米, , 则拉线的长为( )
A、 B、 C、 D、5. 如图,是电杆的一根拉线,测得米, , 则拉线的长为( )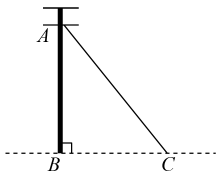 A、米 B、米 C、米 D、米6. 如图,AB表示一条跳台滑雪赛道,在点A处测得起点B的仰角为35°,底端点C与顶端点B的距离为50米,则赛道AB的长度为( )米.
A、米 B、米 C、米 D、米6. 如图,AB表示一条跳台滑雪赛道,在点A处测得起点B的仰角为35°,底端点C与顶端点B的距离为50米,则赛道AB的长度为( )米. A、 B、 C、 D、7. 如图,O为跷跷板AB的中点.支柱OC与地面MN垂直,垂足为点C,当跷跷板的一端B着地时,跷跷板AB与地面MN的夹角为20°,测得AB=1.6m,则OC的长为( )
A、 B、 C、 D、7. 如图,O为跷跷板AB的中点.支柱OC与地面MN垂直,垂足为点C,当跷跷板的一端B着地时,跷跷板AB与地面MN的夹角为20°,测得AB=1.6m,则OC的长为( )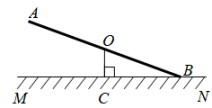 A、 B、 C、 D、8. 如图,是线段AB在投影面P上的正投影, , , 则投影的长为( )
A、 B、 C、 D、8. 如图,是线段AB在投影面P上的正投影, , , 则投影的长为( ) A、 B、 C、 D、9. 如图,为了测量河岸A、B两地间的距离,在与AB垂直的方向上取点C,测得AC=a, , 那么A、B两地的距离等于( )
A、 B、 C、 D、9. 如图,为了测量河岸A、B两地间的距离,在与AB垂直的方向上取点C,测得AC=a, , 那么A、B两地的距离等于( ) A、 B、 C、 D、10. 如图,某停车场入口的栏杆AB,从水平位置绕点O旋转到A'B'的位置,已知AO的长为4米.若栏杆的旋转角∠AOA'=α,则栏杆A端升高的高度为( )
A、 B、 C、 D、10. 如图,某停车场入口的栏杆AB,从水平位置绕点O旋转到A'B'的位置,已知AO的长为4米.若栏杆的旋转角∠AOA'=α,则栏杆A端升高的高度为( ) A、 B、4sinα C、4cosα D、
A、 B、4sinα C、4cosα D、二、填空题(每题3分,共15分)
-
11. 如图,在中, , 如果 , , 那么的长为 .
 12. 如图,在中, , 于点 , , 那么 .
12. 如图,在中, , 于点 , , 那么 . 13. 如图,在等腰直角中, , 点D是AC上一点,如果 , , 那么AB的长为 .
13. 如图,在等腰直角中, , 点D是AC上一点,如果 , , 那么AB的长为 . 14. 如图,测得某医院的自动扶梯的长为m,自动扶梯与地面所成的角为α,则该自动扶梯到达的高度n为.
14. 如图,测得某医院的自动扶梯的长为m,自动扶梯与地面所成的角为α,则该自动扶梯到达的高度n为. 15. 如图,河岸AD,BC互相平行,桥AB垂直于两岸,从C处看桥的两端A,B,夹角∠BCA=60°,测得BC=14m,则桥长AB=m(结果精确到1m).
15. 如图,河岸AD,BC互相平行,桥AB垂直于两岸,从C处看桥的两端A,B,夹角∠BCA=60°,测得BC=14m,则桥长AB=m(结果精确到1m).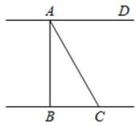
三、解答题(共7题,共55分)
-
16. 如图,在中, , , , 求AC的长和的值.
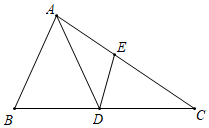
 17. 如图,中, , , D为边延长线上一点, , 求的值.
17. 如图,中, , , D为边延长线上一点, , 求的值. 18. 如图,在△ABC中,tanA= ,∠B=45°,AB=14.求BC的长.
18. 如图,在△ABC中,tanA= ,∠B=45°,AB=14.求BC的长. 19. 如图,是的高,若 , , .
19. 如图,是的高,若 , , . (1)、求边的长;(2)、求的值.20. 如图,在矩形ABCD中,点E为边AB上的一动点(点E不与点A,B重合),连接DE,过点C作CF⊥DE,垂足为F.
(1)、求边的长;(2)、求的值.20. 如图,在矩形ABCD中,点E为边AB上的一动点(点E不与点A,B重合),连接DE,过点C作CF⊥DE,垂足为F. (1)、求证:△ADE∽△FCD;(2)、若AD=6,tan∠DCF= , 求AE的长.
(1)、求证:△ADE∽△FCD;(2)、若AD=6,tan∠DCF= , 求AE的长.