【培优卷】1.3三角函数的计算—北师大版数学九年级下册同步测试
试卷更新日期:2023-09-17 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,在△ABC中,∠C=90°,∠B=42°37',BC=8,若用科学计算器求AC的长,则下列按键顺序正确的是( )
 A、
A、
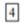


 B、
B、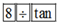
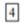


 C、
C、

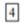


 D、
D、


 2. 用科学记算器算得①293=24389;② ≈7.615773106;③sin35°≈0.573576436;④若tana=5,则锐角a≈0.087488663°.其中正确的是( )A、①②③ B、①②④ C、②③④ D、①③④3. 锐角 满足 ,利用计算器求 时,依次按键 ,则计算器上显示的结果是( )A、 B、 C、 D、4. 利用计算器求值时,小明将按键顺序为
2. 用科学记算器算得①293=24389;② ≈7.615773106;③sin35°≈0.573576436;④若tana=5,则锐角a≈0.087488663°.其中正确的是( )A、①②③ B、①②④ C、②③④ D、①③④3. 锐角 满足 ,利用计算器求 时,依次按键 ,则计算器上显示的结果是( )A、 B、 C、 D、4. 利用计算器求值时,小明将按键顺序为 的显示结果为a,
的显示结果为a,  的显示结果为b,则a与b的乘积为( ) A、﹣16 B、16 C、﹣9 D、95. 在计算器上,小明将按键顺序的显示结果记为a,的显示结果记为b,则a与b的乘积为( )A、 B、 C、 D、66. 下列说法正确的是( )A、求sin30°的按键顺序是
的显示结果为b,则a与b的乘积为( ) A、﹣16 B、16 C、﹣9 D、95. 在计算器上,小明将按键顺序的显示结果记为a,的显示结果记为b,则a与b的乘积为( )A、 B、 C、 D、66. 下列说法正确的是( )A、求sin30°的按键顺序是 、30、=
B、求23的按键顺序
、30、=
B、求23的按键顺序  、2、
、2、  、3、=
C、求的按键顺序是
、3、=
C、求的按键顺序是  、
、  、8、=
D、已知sinA=0.5018,用计算器求锐角A的大小,按键顺序是
、8、=
D、已知sinA=0.5018,用计算器求锐角A的大小,按键顺序是  、
、  、0.5018、=
7. 下列关于运用计算器的说法错误的是( ).A、用计算器计算时,在按、、这三种键之前应先按键 B、要启动计算器的统计计算功能应按的键是 C、启动计算器的统计计算功能后,要清除原有统计数据应按键 D、用计算器计算时,依次按键显示结果是0.58. 如图,有一个山坡,如果沿山坡在水平AC方向上每前进100m铅直高度就升高60m,那么用科学计算器求坡角∠A的度数,并以“度、分、秒”为单位表示出这个度数,下列按键顺序正确的是( )
、0.5018、=
7. 下列关于运用计算器的说法错误的是( ).A、用计算器计算时,在按、、这三种键之前应先按键 B、要启动计算器的统计计算功能应按的键是 C、启动计算器的统计计算功能后,要清除原有统计数据应按键 D、用计算器计算时,依次按键显示结果是0.58. 如图,有一个山坡,如果沿山坡在水平AC方向上每前进100m铅直高度就升高60m,那么用科学计算器求坡角∠A的度数,并以“度、分、秒”为单位表示出这个度数,下列按键顺序正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 如图,某商场有一自动扶梯,其倾斜角为 , 高为7米.用计算器求的长,下列按键顺序正确的是( )
9. 如图,某商场有一自动扶梯,其倾斜角为 , 高为7米.用计算器求的长,下列按键顺序正确的是( )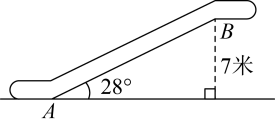 A、
A、 B、
B、 C、
C、 D、
D、 10. 2022年2月4日在北京举办了第24届冬季奥运会,很多学校都开展冰雪项目学习,如图,一位同学乘滑雪板沿斜坡笔直滑下100米,若斜坡的坡比为 , 用计算器求下滑的水平距离,则下列按键顺序正确的是( )
10. 2022年2月4日在北京举办了第24届冬季奥运会,很多学校都开展冰雪项目学习,如图,一位同学乘滑雪板沿斜坡笔直滑下100米,若斜坡的坡比为 , 用计算器求下滑的水平距离,则下列按键顺序正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题(每空1分,共18)
-
11. 填空:
sin15°=cos≈(精确到0.0001);
cos63°=sin≈(精确到0.0001);
sin(90°-α)= , cos(90°-α)=(α为锐角).
12. 用计算器求下列各式的值 精确到 .(1)、 ;(2)、 .13. 如图,在Rt△ABC中,∠C=90°. (1)、若AC=5,BC=12,则AB= , tanA= , ∠A≈(精确到1″);(2)、若AC=3,AB=5,则sinA= , tanB= , ∠A≈ , ∠B≈(精确到1″).14. 一个梯子斜靠在墙上,已知梯子长 米,梯子位于地面上的一端距离墙壁2.5米,则梯子与地面所成锐角的度数为.(用科学计算器计算,结果精确到 分)15. 请从以下两个小题中任选一个作答.
(1)、若AC=5,BC=12,则AB= , tanA= , ∠A≈(精确到1″);(2)、若AC=3,AB=5,则sinA= , tanB= , ∠A≈ , ∠B≈(精确到1″).14. 一个梯子斜靠在墙上,已知梯子长 米,梯子位于地面上的一端距离墙壁2.5米,则梯子与地面所成锐角的度数为.(用科学计算器计算,结果精确到 分)15. 请从以下两个小题中任选一个作答.A:如图,AD是正五边形ABCDE的一条对角线,则∠BAD=.
B:用科学计算器计算: +3tan56°≈.(结果精确到0.01)

三、解答题(共7题,共52分)
-
16. 利用计算器求满足下列条件的锐角 的度数.(精确到 )(1)、 ;(2)、 ;(3)、 ;(4)、 .17. 利用计算器求下列各式的值:(1)、 ;(2)、 ;(3)、 ;(4)、18. 如图,一名患者体内某重要器官后面有一肿瘤.在接受放射性治疗时,为了最大限度地保证疗效,并且防止伤害器官,射线必须从侧面照射肿瘤.已知肿瘤在皮下 的A处,射线从肿瘤右侧 的B处进入身体,求射线与皮肤所成的锐角.
 19. 一梯子斜靠在一面墙上.已知梯长 ,梯子位于地面上的一端离墙壁 ,求梯子与地面所成锐角的度数.20. 如图
19. 一梯子斜靠在一面墙上.已知梯长 ,梯子位于地面上的一端离墙壁 ,求梯子与地面所成锐角的度数.20. 如图 (1)、用计算器计算并验证 与 之间的大小关系;(2)、若 , , 都是锐角,猜想 与 之间的大小关系;(3)、请借助如下图形证明上述猜想.21. 如图所示,一种适用于笔记本电脑的铝合金支架,边 , 可绕点 开合,在 边上有一固定点 ,支柱 可绕点 转动,边 上有六个卡孔,其中离点 最近的卡孔为 ,离点 最远的卡孔为 .当支柱端点 放入不同卡孔内,支架的倾斜角发生变化.将电脑放在支架上,电脑台面的角度可达到六档调节,这样更有利于工作和身体健康.现测得 的长为 , 为 ,支柱 为 .
(1)、用计算器计算并验证 与 之间的大小关系;(2)、若 , , 都是锐角,猜想 与 之间的大小关系;(3)、请借助如下图形证明上述猜想.21. 如图所示,一种适用于笔记本电脑的铝合金支架,边 , 可绕点 开合,在 边上有一固定点 ,支柱 可绕点 转动,边 上有六个卡孔,其中离点 最近的卡孔为 ,离点 最远的卡孔为 .当支柱端点 放入不同卡孔内,支架的倾斜角发生变化.将电脑放在支架上,电脑台面的角度可达到六档调节,这样更有利于工作和身体健康.现测得 的长为 , 为 ,支柱 为 .
 (1)、当支柱的端点 放在卡孔 处时,求 的度数;(2)、当支柱的端点 放在卡孔 处时, ,若相邻两个卡孔的距离相同,求此间距.(结果精确到十分位)22. 今年疫情期间,针对各种入口处人工测量体温存在的感染风险高、效率低等问题,清华大学牵头研制一款“测温机器人”,如图1,机器人工作时,行人抬手在测温头处测量手腕温度,体温合格则机器人抬起臂杆行人可通行,不合格时机器人不抬臂杆并报警,从而有效阻隔病原体.
(1)、当支柱的端点 放在卡孔 处时,求 的度数;(2)、当支柱的端点 放在卡孔 处时, ,若相邻两个卡孔的距离相同,求此间距.(结果精确到十分位)22. 今年疫情期间,针对各种入口处人工测量体温存在的感染风险高、效率低等问题,清华大学牵头研制一款“测温机器人”,如图1,机器人工作时,行人抬手在测温头处测量手腕温度,体温合格则机器人抬起臂杆行人可通行,不合格时机器人不抬臂杆并报警,从而有效阻隔病原体. (1)、为了设计“测温机器人”的高度,科研团队采集了大量数据.下表是抽样采集某一地区居民的身高数据:
(1)、为了设计“测温机器人”的高度,科研团队采集了大量数据.下表是抽样采集某一地区居民的身高数据:测量对象
男性(18~60岁)
女性(18~55岁)
抽样人数(人)
2000
5000
20000
2000
5000
20000
平均身高(厘米)
173
175
176
164
165
164
根据你所学的知识,若要更准确的表示这一地区男、女的平均身高,男性应采用厘米,女性应采用厘米;
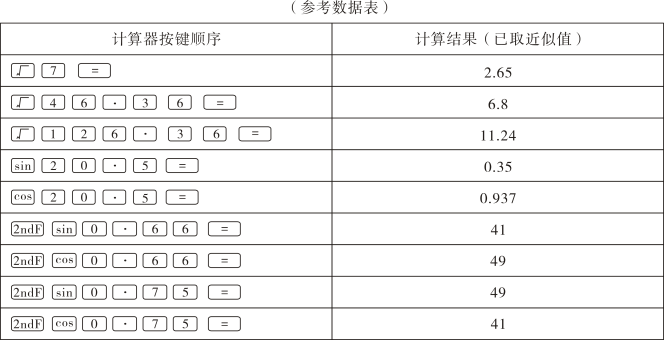
(2)、如图2,一般的,人抬手的高度与身高之比为黄金比时给人的感觉最舒适,由此利用(1)中的数据得出测温头点P距地面105厘米.指示牌挂在两臂杆AB,AC的连接点A处,A点距地面110厘米.臂杆落下时两端点B,C在同一水平线上,BC=100厘米,点C在点P的正下方5厘米处.若两臂杆长度相等,求两臂杆的夹角.(参考数据表)
计算器按键顺序
计算结果(近似值)
计算器按键顺序
计算结果(近似值)
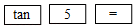
0.1

78.7
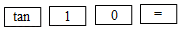
0.2

84.3

1.7
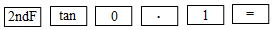
5.7

3.5
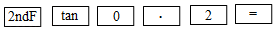
11.3