【提升卷】1.2 30°、45°、60°角的三角函数值—2023-2024学年北师大版九年级下册同步测试

试卷更新日期：2023-09-16 类型：同步测试

进入出卷网下载

一、选择题

1. 下列运算中，值为 $\frac{1}{4}$ 的是（）．

A、 $s i n 45 ° \times c o s 45 °$ B、 $t a n 45 ° - c o s^{2} 30 °$ C、 $\frac{t a n 30 °}{c o s 60 °}$ D、 ${(t a n 60 °)}^{- 1}$

查看试题解析
2. 在 $△ A B C$ 中， $∠ B$ ， $∠ C$ 都是锐角， $t a n B = 1$ ， $c o s C = \frac{\sqrt{2}}{2}$ ，则对 $△ A B C$ 的形状最确切的判断是（）

A、锐角三角形 B、等腰直角三角形 C、等腰三角形 D、直角三角形

查看试题解析
3. 点 $(- \sin 60 ° ， \cos 60 °)$ 关于y轴对称的点的坐标是（）

A、 $(\frac{\sqrt{3}}{2} ， \frac{1}{2})$ B、 $(- \frac{\sqrt{3}}{2} ， \frac{1}{2})$ C、 $(- \frac{\sqrt{3}}{2} ， - \frac{1}{2})$ D、 $(\frac{1}{2} ， \frac{3}{2})$

查看试题解析
4. 已知 $α$ 是锐角， $2 c o s (α + 45 °) = 1$ ，则 $α$ 的值是（）

A、 $15 °$ B、 $30 °$ C、 $45 °$ D、 $60 °$

查看试题解析
5. 已知锐角α满足tan（α+10°）=1，则锐用α的度数为（）

A、20° B、35° C、45° D、50°

查看试题解析
6. 若数轴上tan30°的值用一个点表示，这个点的位置可能落在段（）

A、① B、② C、③ D、④

查看试题解析
7. 在直角三角形ABC中， $∠ C = 90 ° ， A B = 4 ， B C = 2 \sqrt{3}$ ，则 $3 t a n \frac{A}{2}$ 的值是（）

A、 $\sqrt{3}$ B、 $2 \sqrt{3}$ C、 $3 \sqrt{3}$ D、3

查看试题解析
8. 下列说法中正确的是（）

A、在Rt△ABC中，若tanA＝ $\frac{3}{4}$ ，则a＝4，b＝3 B、在Rt△ABC中，∠C＝90°，若a＝3，b＝4，则tanA＝ $\frac{3}{4}$ C、tan30°＋tan60°＝1 D、tan75°＝tan(45°＋30°)＝tan45°＋tan30°＝1＋ $\frac{\sqrt{3}}{3}$

查看试题解析
9. 如图坐标系中，O（0，0），A（3，3 $\sqrt{3}$ ），B（6，0），将△OAB沿直线CD折叠，使点A恰好落在线段OB上的点E处，若OE＝ $\frac{6}{5}$ ，则AC：AD的值是（）

A、1：2 B、2：3 C、6：7 D、7：8

查看试题解析
10. 在矩形 $A B C D$ 中，有一个菱形 $B F D E$ （点 $E$ 、 $F$ 分别在线段 $A B$ 、 $C D$ 上），记它们的面积分别为 $S_{A B C D}$ 和 $S_{B F D E}$ ，现给出下列命题：①若 $\frac{S_{A B C D}}{S_{B F D E}} = \frac{2 + \sqrt{3}}{2}$ ，则 $t a n ∠ E D F = \frac{\sqrt{3}}{3}$ ， ②若 $D E^{2} = B D \cdot E F$ ，则 $D F = 2 A D$ .则（）.

A、①是真命题，②是真命题 B、①是真命题，②是假命题 C、①是假命题，②是真命题 D、①是假命题，②是假命题

查看试题解析

二、填空题

11. 若 $\tan 35 ° \cdot \tan α \cdot \tan 50 ° \cdot \tan 55 ° = 1$ ，则锐角 $α =$ °．

查看试题解析
12. 关于x的一元二次方程 $x^{2} － 2 x$ +tanα=0有两个相等的实数根，则锐角α = ．

查看试题解析
13. 已知a＝3，且 ${(4 \tan 45 ° - b)}^{2} + \sqrt{3 + \frac{1}{2} b - c} = 0$ ，则以a、b、c为边长的三角形面积等于．

查看试题解析
14. 如图，点A、B分别在反比例函数 $y = \frac{1}{x} (x > 0)$ 、 $y = \frac{k}{x} (x > 0)$ 的图象上，且 $∠ A O B = 90 °$ ， $s i n B = \frac{1}{2}$ ，则 $k =$

查看试题解析
15. 定义一种运算： $s i n (α + β) = s i n α c o s β + c o s α s i n β$ ， $s i n (α - β) = s i n α c o s β - c o s α s i n β$ ．例如：当 $α = 60 °$ ， $β = 45 °$ 时， $s i n (60 ° - 45 °) = \frac{\sqrt{3}}{2} \times \frac{\sqrt{2}}{2} - \frac{1}{2} \times \frac{\sqrt{2}}{2} = \frac{\sqrt{6} - \sqrt{2}}{4}$ ，则 $s i n 75 °$ 的值为．

查看试题解析

三、计算题

16. 计算：

(1)、 $\sqrt{(1 - t a n 60 °)^{2}} - 4 c o s 30 ° + 202 2^{0}$

(2)、已知 $α$ 为锐角， $s i n (α + 15 °) = \frac{\sqrt{3}}{2}$ ，计算 $\sqrt{8} - 4 c o s α + t a n α + {(\frac{1}{3})}^{- 1}$ 的值．

查看试题解析
17. 已知 $α$ 是锐角，且 $s i n (α - 15 °) = \frac{\sqrt{2}}{2}$ ，计算 $\sqrt{4} - 4 c o s α - | 1 - 2 s i n α | + t a n α$ 的值.

查看试题解析
18.

(1)、计算：2tan60°·tan30°﹣4cos²45°+sin60°；

(2)、如图，在△ABC中，tanC＝ $\frac{3}{5}$ ，点D在边BC上，AB＝AD，CD＝2BD＝4，求sinB的值．

查看试题解析
19. 在 $△ A B C$ 中， $A B = 6$ ， $B C = 4$ ， $∠ B$ 为锐角且 $c o s B = \frac{1}{2}$ .

(1)、求 $∠ B$ 的度数；

(2)、求 $∠ C$ 的正切值.

查看试题解析
20. 图①、图②均是6×6的正方形网格，每个小正方形的顶点称为格点.线段AB的端点均在格点上，按下列要求画出图形.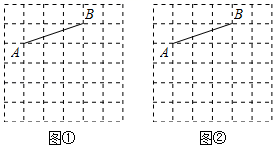

（ 1 ）在图①中找到两个格点C，使∠BAC是锐角，且tan∠BAC＝ $\frac{1}{3}$ ；

（ 2 ）在图②中找到两个格点D，使∠ADB是锐角，且tan∠ADB＝1.

查看试题解析
21. 对钝角α，定义三角函数值如下：
sinα＝sin(180°－α)，cosα＝－cos(180°－α)．

(1)、求sin120°，cos120°的值；

(2)、若一个钝角三角形的三个内角比是1：1：4，点A，B是这个三角形的两个顶点，sinA，cosB是方程4x²－mx－1＝0的两个不相等的实数根，求m的值及∠A和∠B的度数．

查看试题解析
22. 阅读材料：关于三角函数有如下的公式：sin（α+β）＝sinαcosβ+cosαsinβ，tan（α+β） $= \frac{tan α + tan β}{1 - tan α tan β}$ .利用这些公式可以将两角和的三角函数值转化成两个三角函数值的和（差），如tan75°＝tan（30°+45°） $= \frac{tan 45 ° + tan 30 °}{1 - tan 45 ° + tan 30 °} = \frac{1 + \frac{\sqrt{3}}{3}}{1 - 1 \times \frac{\sqrt{3}}{3}} = \frac{3 + \sqrt{3}}{3 - \sqrt{3}} =$ 2 $+ \sqrt{3}$ .
问题解决：根据以上阅读材料，请选择适当的公式解答下列问题

(1)、求sin75°；

(2)、如图，边长为2的正 $△$ ABC沿直线滚动设当 $△$ ABC滚动240°时，C点的位置在 $C^{'}$ ，当 $△$ ABC滚动480°时，A点的位置在 $A^{'}$ .
①求tan∠ $C A C^{'}$ 的值；

②试确定 $∠ C A C^{'} + ∠ C A A^{'}$ 的度数.

查看试题解析