【培优卷】1.2 30°、45°、60°角的三角函数值—北师大版数学九年级下册同步测试
试卷更新日期:2023-09-16 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O顺时针旋转75°至OA′B′C′的位置,若OB= , ∠C=120°,则点B′的坐标为( )
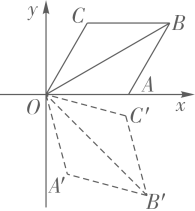 A、(3,) B、(3,-) C、( , ) D、( , -)2. 由4个形状相同,大小相等的菱形组成如图所示的网格,菱形的顶点称为格点,点A,B,C都在格点上,∠O=60°,则tan∠ABC=( )
A、(3,) B、(3,-) C、( , ) D、( , -)2. 由4个形状相同,大小相等的菱形组成如图所示的网格,菱形的顶点称为格点,点A,B,C都在格点上,∠O=60°,则tan∠ABC=( ) A、 B、 C、 D、3. 在矩形ABCD中有一个菱形BEDF(点E,F分别在线段AB、CD上),记它们的面积分别为S矩形ABCD和S菱形BEDF,若S矩形ABCD:S菱形BEDF=(2+):2,则=( )
A、 B、 C、 D、3. 在矩形ABCD中有一个菱形BEDF(点E,F分别在线段AB、CD上),记它们的面积分别为S矩形ABCD和S菱形BEDF,若S矩形ABCD:S菱形BEDF=(2+):2,则=( ) A、 B、2 C、 D、4. 如图,在▱OABC中,边OC在x轴上,点A(1,),点C(3,0).按以下步骤作图:分别以点B,C为圆心,大于BC的长为半径作弧,两弧相交于E,F两点;作直线EF,交AB于点H;连接OH,则OH的长为( )
A、 B、2 C、 D、4. 如图,在▱OABC中,边OC在x轴上,点A(1,),点C(3,0).按以下步骤作图:分别以点B,C为圆心,大于BC的长为半径作弧,两弧相交于E,F两点;作直线EF,交AB于点H;连接OH,则OH的长为( ) A、 B、 C、2 D、25. 如图,在Rt△ABC中,∠ACB=90°,AC=3,D是边AB上一点,连结CD,将△ACD沿CD翻折得到△ECD,连结BE.若四边形BCDE是平行四边形,则BC的长为( )
A、 B、 C、2 D、25. 如图,在Rt△ABC中,∠ACB=90°,AC=3,D是边AB上一点,连结CD,将△ACD沿CD翻折得到△ECD,连结BE.若四边形BCDE是平行四边形,则BC的长为( )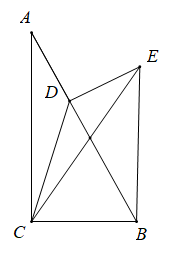 A、 B、3 C、2 D、36. 如图,在平面直角坐标系中, 的顶点B在x轴的正半轴上, ,点A的坐标为 ,将 绕点О逆时针旋转,使点B的对应点 落在边OA上,则 的坐标为( )
A、 B、3 C、2 D、36. 如图,在平面直角坐标系中, 的顶点B在x轴的正半轴上, ,点A的坐标为 ,将 绕点О逆时针旋转,使点B的对应点 落在边OA上,则 的坐标为( ) A、 B、 C、 D、7. 如图,矩形OABC的顶点O( 0,0),B(-2,2 ),若矩形绕点O逆时针旋转,每秒旋转60°,则第145秒时,矩形的对角线交点D的坐标为( )
A、 B、 C、 D、7. 如图,矩形OABC的顶点O( 0,0),B(-2,2 ),若矩形绕点O逆时针旋转,每秒旋转60°,则第145秒时,矩形的对角线交点D的坐标为( ) A、(-1, ) B、(-1,-3) C、(-2,0 ) D、(1,-3)8. 如图,在平行四边形OABC中,边OC在x轴上,点A(1,),点C(3,0).按以下步骤作图:分别以点B,C为圆心,大于BC的长为半径作弧,两弧相交于E,F两点;作直线EF,交AB于点H;连接OH,则OH的长为( )
A、(-1, ) B、(-1,-3) C、(-2,0 ) D、(1,-3)8. 如图,在平行四边形OABC中,边OC在x轴上,点A(1,),点C(3,0).按以下步骤作图:分别以点B,C为圆心,大于BC的长为半径作弧,两弧相交于E,F两点;作直线EF,交AB于点H;连接OH,则OH的长为( ) A、 B、 C、2 D、29. 如图,在平行四边形ABCD和平行四边形BEFG中,AB=AD,BG=BE,点A, B, E在同一直线上,P是线段DF的中点,连接PG、PC,若∠ABC=∠BEF=60°,则 =( )
A、 B、 C、2 D、29. 如图,在平行四边形ABCD和平行四边形BEFG中,AB=AD,BG=BE,点A, B, E在同一直线上,P是线段DF的中点,连接PG、PC,若∠ABC=∠BEF=60°,则 =( ) A、 B、 C、 D、10. 如图,正△AOB的边长为5,点B在x轴正半轴上,点A在第一象限,反比例函数y= (x>0)的图象分别交边AO,AB于点C,D,若OC=2BD,则实数k的值为( )
A、 B、 C、 D、10. 如图,正△AOB的边长为5,点B在x轴正半轴上,点A在第一象限,反比例函数y= (x>0)的图象分别交边AO,AB于点C,D,若OC=2BD,则实数k的值为( )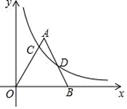 A、4 B、 C、 D、8
A、4 B、 C、 D、8二、填空题(每题3分,共15分)
-
11. 在△ABC中,AB = AC = 5,tanB = . 若⊙O的半径为 ,且⊙O经过点B与C , 那么线段OA的长等于.12. 如图,中, , , 以边上的中线为折痕将折叠,使点A落在点D处,如果恰好与垂直,则的值为 .
 13. 如图,在矩形ABCD中,AB=2,BC=2 ,点M、N分别在AD,BC上,且AM=CN,点P在CD上(且不与点D,C重合),当MP+PN最小时,tan∠MPN的值是.
13. 如图,在矩形ABCD中,AB=2,BC=2 ,点M、N分别在AD,BC上,且AM=CN,点P在CD上(且不与点D,C重合),当MP+PN最小时,tan∠MPN的值是. 14. 如图,点A在反比例函数y= (x>0)的图象上,点B在反比例函数y= (k<0)的图象上,且OA⊥OB,线段AB交反比例函数y= (x>0) 的图象于另一点C,连结OC。若点C为AB的中点,tan∠OCA= ,则k的值为。
14. 如图,点A在反比例函数y= (x>0)的图象上,点B在反比例函数y= (k<0)的图象上,且OA⊥OB,线段AB交反比例函数y= (x>0) 的图象于另一点C,连结OC。若点C为AB的中点,tan∠OCA= ,则k的值为。 15. 已知 , (其中 和 都表示角度),比如求 ,可利用公式得 ,又如求 ,可利用公式得 ,请你结合材料,若 ( 为锐角),则 的度数是 .
15. 已知 , (其中 和 都表示角度),比如求 ,可利用公式得 ,又如求 ,可利用公式得 ,请你结合材料,若 ( 为锐角),则 的度数是 .三、解答题(共7题,共55分)
-
16.(1)、在计算时,小亮的计算过程如下:
解:
小莹发现小亮的计算有误,帮助小亮找出了3个错误.请你找出其他错误,参照①~③的格式写在横线上,并依次标注序号:
①;②;③;
请写出正确的计算过程.
(2)、先化简,再求值: , 其中x是方程的根.17. 已知,矩形中,点F在上,连接交于点E. (1)、若于点E,如图1.
(1)、若于点E,如图1.①证明:;
②若 , 求的度数;
(2)、若 , 点F是的中点,连接 , 如图2,求的值.18. 如图,在平面直角坐标系中,已知 ,点P为线段 外一动点,且 .点B为x轴上一点,现在以B为中心,将 顺时针旋转 至 ,连接 .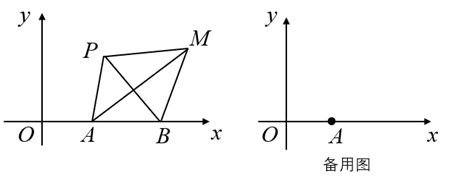 (1)、求证: 为等边三角形;(2)、当 轴, 时,求 的长;(3)、当点B的坐标为 时,求线段 的最大值(直接写出结果即可).19.(1)、课本再现
(1)、求证: 为等边三角形;(2)、当 轴, 时,求 的长;(3)、当点B的坐标为 时,求线段 的最大值(直接写出结果即可).19.(1)、课本再现如图1,在和中, , , ,
求证: . 我们在数学课上探索这一结论时进行了分析:要证 , 可设法证 , 若设 , 则只需证 .

请你根据以上分析,完成证明.
(2)、知识应用如图2,在四边形中, , , , 求的度数.
 20. 已知点E在△ABC内,∠ABC=∠EBD=α,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°.
20. 已知点E在△ABC内,∠ABC=∠EBD=α,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°.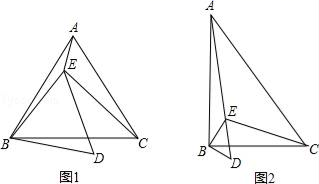 (1)、当α=60°时(如图1),
(1)、当α=60°时(如图1),①判断△ABC的形状,并说明理由;
②求证:BD= AE;
(2)、当α=90°时(如图2),求 的值.21. 如图,Rt△ABC中,∠C=90°,E是AB边上一点,D是AC边上一点,且点D不与A、C重合,ED⊥AC.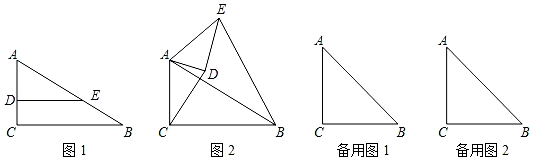 (1)、当sinB= 时,
(1)、当sinB= 时,①求证:BE=2CD;
②当△ADE绕点A旋转到如图2的位置时(45°<∠CAD<90°).BE=2CD是否成立?若成立,请给出证明;若不成立.请说明理由.
(2)、当sinB= 时,将△ADE绕点A旋转到∠DEB=90°,若AC=10,AD=2 ,求线段CD的长.22. 某校组织数学兴趣探究活动,爱思考的小实同学在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”.如图1、图2、图3中, 、 是 的中线, 于点 ,像 这样的三角形均称为“中垂三角形”.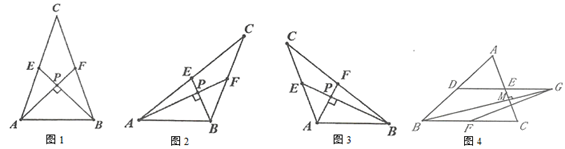 (1)、(特例探究)
(1)、(特例探究)如图1,当 , 时, , ;
如图2,当 , 时, , ;
(2)、(归纳证明)请你观察(1)中的计算结果,猜想 、 、 三者之间的关系,用等式表示出来,并利用图3证明你的结论;
(3)、(拓展证明)如图4,在 中, , , 、 、 分别是边 、 的中点,连结 并延长至 ,使得 ,连结 ,当 于点 时,求 的长.