【提升卷】1.1锐角三角函数—2023-2024学年北师大版九年级下册同步测试

试卷更新日期：2023-09-16 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如图，点 $A ， B ， C$ 在正方形网格的格点上，则 $s i n ∠ B A C =$ （）

A、 $\frac{\sqrt{13}}{13}$ B、 $\frac{\sqrt{6}}{6}$ C、 $\frac{\sqrt{26}}{13}$ D、 $\frac{\sqrt{26}}{26}$

查看试题解析
2. 在 $△ A B C$ 中， $∠ C = 90 °$ ， $s i n B = \frac{4}{5}$ ，则 $t a n B$ 值为（）

A、 $\frac{4}{3}$ B、 $\frac{3}{4}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
3. 如图，已知：45°＜A＜90°，则下列各式成立的是（）

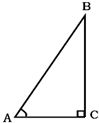A、sinA=cosA B、sinA＞cosA C、sinA＞tanA D、sinA＜cosA

查看试题解析
4. 如果方程x²﹣8x+15＝0的两个根分别是Rt△ABC的两条边，△ABC最小的角为A，那么tanA的值为（）

A、 $\frac{3}{4}$ B、 $\frac{3}{5}$ C、 $\frac{4}{5}$ D、 $\frac{3}{4}$ 或 $\frac{3}{5}$

查看试题解析
5. 在 $R t △ A B C$ 中， $∠ C = 9 0^{∘}$ ， $∠ B = 3 5^{∘}$ ， $A B = 7$ ，则 $B C$ 的长为（）

A、 $7 s i n 3 5^{∘}$ B、 $7 c o s 3 5^{∘}$ C、 $7 t a n 3 5^{∘}$ D、 $\frac{7}{c o s 3 5^{∘}}$

查看试题解析
6. 如图，某商场有一自动扶梯，其倾斜角为α，高为h米，扶梯的长度是（）

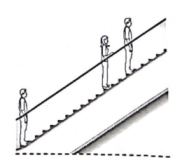A、 $\frac{h}{t a n α}$ B、hcosα C、hsinα D、 $\frac{h}{s i n α}$

查看试题解析
7. 下列各式中正确的是（）

A、 $\sin 46 ° - \cos 44 °$ B、 $2 \sin 40 ° - \sin 80 °$ C、 $\cos 44 ° < \cos 46 °$ D、 $\sin^{2} 44 ° + \sin^{2} 46 ° = 1$

查看试题解析
8. 如图，梯子（长度不变）跟地面所成的锐角为A，关于∠A的三角函数值与梯子的倾斜程度之间，叙述正确的是（）

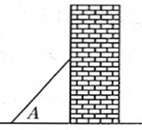A、sinA的值越大，梯子越陡 B、cosA的值越大，梯子越陡 C、tanA的值越小，梯子越陡 D、陡缓程度与∠A的三角函数值无关

查看试题解析
9. 将一矩形纸片ABCD沿CE折叠，B点恰好落在AD边上的F处，若 $A B ： B C = 4 ： 5$ ，则 $\cos ∠ A F E$ 的值为（）

A、 $\frac{5}{4}$ B、 $\frac{3}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{5}$

查看试题解析
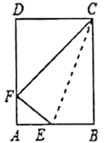10. 矩形纸片 $A B C D$ 中， $B C = 2 A B$ ，将纸片对折，使顶点A与顶点C重合，得折痕 $E F$ ，将纸片展开铺平后再进行折叠，使顶点B与顶点D重合，得折痕 $M N$ ，展开铺平后如图所示.若折痕 $E F$ 与 $M N$ 较小的夹角记为 $θ$ ，则 $t a n θ$ 的值是（）

A、 $\frac{4}{5}$ B、 $\frac{5}{4}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析

二、填空题（每题3分，共15分）

11. 选“＜、=或＞”中合适的符号填空：sin20°sin70°，sin50°cos40°.

查看试题解析
12. 如图，P是∠α的边OA上一点，且P点的坐标为（3，4），则sin（90°﹣α）= ．

查看试题解析
13. 在△ABC中，AB=AC=5，BC=8，若∠BPC= $\frac{1}{2}$ ∠BAC，tan∠BPC= ．

查看试题解析
14. 如图，在矩形纸片 $A B C D$ 中， $A B = 5$ ， $B C = 3$ ，将 $△ B C D$ 沿 $B D$ 折叠到 $△ B E D$ 位置， $D E$ 交 $A B$ 于点F，则 $s i n ∠ A D F$ 的值为.

查看试题解析
15. 如图，在 $Δ A B C$ 中， $D C$ 平分 $∠ A C B$ ， $B D ⊥ C D$ 于点D， $∠ A B D = ∠ A$ ，若 $B D = 1$ ， $A C = 7$ ，则 $c o s ∠ C B D$ 的值为.

查看试题解析

三、解答题（共8题，共55分）

16. 已知：如图，在△ABC中，CD⊥AB，sinA = $\frac{4}{5}$ ， CD =4，AB =5，求AD的长和tanB的值.

查看试题解析
17. 如图，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ，延长斜边BC到点D，使 $C D = \frac{1}{2} B C$ ，联结AD，如果 $t a n B = \frac{4}{3}$ ，求 $t a n ∠ C A D$ 的值．

查看试题解析
18. 如图，矩形ABCD中，M为BC上一点，EM⊥AM交AD的延长线于点E.
①求证：△ABM∽△EMA.
②若AB＝4，BM＝3，求sinE的值.

查看试题解析
19. 如图，在平行四边形 $A B C D$ 中， $D E ⊥ A B$ 于点 $E$ ， $D F ⊥ B C$ 于点 $F$ ，平行四边形 $A B C D$ 的周长为 28，面积为 40， $A B ： A D = 4 ： 3$ ．求：

(1)、 $D E$ 的长；

(2)、 $s i n ∠ E D F$ 的值．

查看试题解析
20. 如图，矩形ABCD中，M为BC上一点，EM⊥AM交AD的延长线于点E．

(1)、求证：△ABM∽△EMA．

(2)、若AB＝4，BM＝3，求sinE的值．

查看试题解析
21. 如图，矩形 $A B C D$ 中， $B C > A B$ ， E是 $A D$ 上一点， $△ A B E$ 沿 $B E$ 折叠，点A恰好落在线段 $C E$ 的点F处，连接 $B F$ .

(1)、求证： $B C = C E$ ；

(2)、若 $\frac{A E}{A D} = \frac{1}{5}$ ，则 $c o s ∠ D C E =$ ；

(3)、设 $\frac{A E}{A D} = k$ ， $\frac{A B}{A D} = m$ ，求m与k满足的关系式.

查看试题解析
22. 如图

(1)、如图锐角的正弦值和余弦值都随着锐角的确定而确定，变化而变化，试探索随着锐角度数的增大，它的正弦值和余弦值变化的规律．

(2)、根据你探索到的规律试比较18°，34°，50°，62°，88°，这些锐角的正弦值的大小和余弦值的大小．

(3)、比较大小（在空格处填写“＞”“=”“＜”号），若α=45°，则sinαcosα；若0°＜α＜45°，则sinαcosα；若45°＜α＜90°，sinα cosα．

查看试题解析
23. 如图，已知， $A (0 ， 4)$ ， $B (- 3 ， 0)$ ， $C (2 ， 0)$ ，过A作y轴的垂线交反比例函数 $y = \frac{k}{x}$ 的图象于点D，连接 $C D$ ， $A B ∥ C D$ ．

(1)、证明：四边形 $A B C D$ 为菱形；

(2)、求此反比例函数的解析式；

(3)、求 $s i n ∠ D A C$ 的值．

查看试题解析