【培优卷】1.1锐角三角函数—北师大版数学九年级下册同步测试
试卷更新日期:2023-09-16 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 在边长为1的正方形组成的网格中,线段AB,CD的端点都在格点上,AB,CD交于点E,则tan∠AED的值为( )
 A、1 B、 C、2 D、2. 如图,在矩形中,交于点 , 点在上,连接分别交 , 于点 , . 若 , 则的值是( )
A、1 B、 C、2 D、2. 如图,在矩形中,交于点 , 点在上,连接分别交 , 于点 , . 若 , 则的值是( )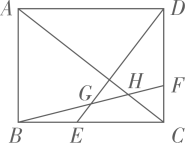 A、 B、 C、 D、3. 如下图,在四边形中, , , , 点分别在边上,若 , 则 ( )
A、 B、 C、 D、3. 如下图,在四边形中, , , , 点分别在边上,若 , 则 ( ) A、 B、 C、 D、4. 如图,在边长为的小正方形网格中,点都在这些小正方形的顶点上,相交于点 , 则( )
A、 B、 C、 D、4. 如图,在边长为的小正方形网格中,点都在这些小正方形的顶点上,相交于点 , 则( ) A、 B、 C、 D、25. 以下说法正确的是( )A、存在锐角 ,使得sin²+cos² >1 B、已知∠A为Rt△ABC的一个内角,且∠A<45°,则sinA<cosA C、在Rt△ABC中,∠C=90°,∠A,∠B为Rt△ABC的两个内角,则sinA不一定等于cosB D、存在锐角 ,使得sin ≥tan6. 如图,在 中, ,分别以AB,AC,BC为边向外作正方形.连结CD,若 ,则 的值为( )
A、 B、 C、 D、25. 以下说法正确的是( )A、存在锐角 ,使得sin²+cos² >1 B、已知∠A为Rt△ABC的一个内角,且∠A<45°,则sinA<cosA C、在Rt△ABC中,∠C=90°,∠A,∠B为Rt△ABC的两个内角,则sinA不一定等于cosB D、存在锐角 ,使得sin ≥tan6. 如图,在 中, ,分别以AB,AC,BC为边向外作正方形.连结CD,若 ,则 的值为( ) A、 B、 C、 D、7. 如图,已知 中, , , 分别为 , 的中点,连结 ,过 作 的平行线与 的角平分线交于点 ,连结 ,若 , ,则 的正弦值为( )
A、 B、 C、 D、7. 如图,已知 中, , , 分别为 , 的中点,连结 ,过 作 的平行线与 的角平分线交于点 ,连结 ,若 , ,则 的正弦值为( ) A、 B、 C、 D、8. 如图,点E在正方形ABCD的边AD上(包括点A和点D)的一个动点,连结BE和CE设y=tan∠BEC,则( )
A、 B、 C、 D、8. 如图,点E在正方形ABCD的边AD上(包括点A和点D)的一个动点,连结BE和CE设y=tan∠BEC,则( )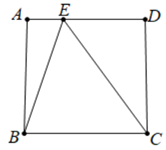 A、y=1 B、y≥1 C、1≤y≤ D、1≤y≤9.
A、y=1 B、y≥1 C、1≤y≤ D、1≤y≤9.如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( )
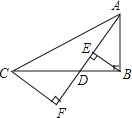 A、不变 B、增大 C、减小 D、先变大再变小10. 如图1,是数学家毕达哥拉斯根据勾股定理所画的“勾股树”.如图2,在Rt△ABC中, , 以其三边为边分别向外作正方形,延长EC,DB分别交GF,AH于点N,K,连接KN交AG于点M,若 , 则为( )
A、不变 B、增大 C、减小 D、先变大再变小10. 如图1,是数学家毕达哥拉斯根据勾股定理所画的“勾股树”.如图2,在Rt△ABC中, , 以其三边为边分别向外作正方形,延长EC,DB分别交GF,AH于点N,K,连接KN交AG于点M,若 , 则为( )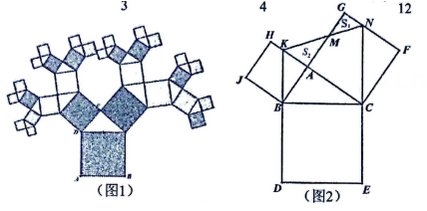 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分,共24分)
-
11. 若三个锐角 满足 ,则 由小到大的顺序为.12. 若α是锐角,且sinα=1﹣3m,则m的取值范围是 ;将cos21°,cos37°,sin41°,cos46°的值,按由小到大的顺序排列是 .
13. 在Rt△ABC中,∠C=90°,若cosB= ,则tanA= , 若此时△ABC的周长为48,那么△ABC的面积 .14. 如图,点E是正方形ABCD的边BC上一点,FG垂直平分AE且分别交AB,AE,BD,CD于点F,H,I,G.若FH=2,IG=6,则HI的长度为 , sin∠FIB的值为 . 15. 如图所示,长宽比为3:2的矩形 , 将矩形沿着折叠,使点落到宽的中点 , 点落到点处,则 .
15. 如图所示,长宽比为3:2的矩形 , 将矩形沿着折叠,使点落到宽的中点 , 点落到点处,则 . 16. 直线y=-x+2a(常数)和双曲线的图象有且只有一个交点B,一次函数y=-x+2a与x轴交于点A,点P是线段OA上的动点,点Q在反比例函数图象上,且满足∠BPO=∠QPA.设PQ与线段AB的交点为M,若OM⊥BP,则的值为 .
16. 直线y=-x+2a(常数)和双曲线的图象有且只有一个交点B,一次函数y=-x+2a与x轴交于点A,点P是线段OA上的动点,点Q在反比例函数图象上,且满足∠BPO=∠QPA.设PQ与线段AB的交点为M,若OM⊥BP,则的值为 .
三、解答题(共7题,共66分)
-
17. 中, , 于D , 于E , 交于F
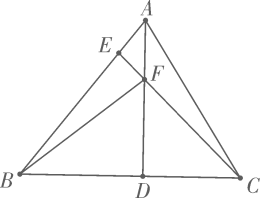 (1)、求证:;(2)、求(用含m的代数式表示);(3)、当时,求的最大值.18. 如图
(1)、求证:;(2)、求(用含m的代数式表示);(3)、当时,求的最大值.18. 如图 (1)、如图1,在中, , 平分 , 交于点 , , 交于点 .
(1)、如图1,在中, , 平分 , 交于点 , , 交于点 .①若 , , 求的长;
②试探究是否为定值.如果是,请求出这个定值;如果不是,请说明理由.
(2)、如图2,和是的2个外角, , 平分 , 交的延长线于点 , , 交的延长线于点记的面积为 , 的面积为 , 的面积为若 , 求的值.19. 已知,在中, , 于点D,点M是射线上一动点(不与C、D重合),连结 , 在下方作 , 连结 , 使 , .(1)、如图,当点M在线段上时,求证:; (2)、如图, , 当点M在线段的延长线上时,交射线于点E.
(2)、如图, , 当点M在线段的延长线上时,交射线于点E.
①试判断与的数量关系和位置关系,并说明理由;
②若 , 求的值.
20. 如图,在矩形ABCD中,AE平分∠BAD交射线BC于点E,过点C作CF⊥AE交射线AE于点F,连结BD交AE于点G,连结DF交射线BC于点H. (1)、当AB<AD时,
(1)、当AB<AD时,①求证:BE=CD,
②猜想∠BDF的度数,并说明理由.
(2)、若时,求tan∠CDF的值(用含k的代数式表示).21.(1)、如图1,纸片中, , , 过点A作 , 垂足为E,沿剪下 , 将它平移至的位置,拼成四边形 , 则四边形的形状为____.(从以下选项中选取) A、正方形 B、菱形 C、矩形(2)、如图2,在(1)中的四边形纸片中,在上取一点F,使 , 剪下 , 将它平移至的位置,拼成四边形 .
A、正方形 B、菱形 C、矩形(2)、如图2,在(1)中的四边形纸片中,在上取一点F,使 , 剪下 , 将它平移至的位置,拼成四边形 .
①求证:四边形是菱形;
②连接 , 求的值.
22. 如图,在矩形中, , 点是边上一动点(点不与 , 重合),连接 , 以为边在直线的右侧作矩形 , 使得矩形矩形 , 交直线于点. (1)、【尝试初探】在点的运动过程中,与始终保持相似关系,请说明理由.(2)、【深入探究】若 , 随着点位置的变化,点的位置随之发生变化,当是线段中点时,求的值.(3)、【拓展延伸】连接 , , 当是以为腰的等腰三角形时,求的值(用含的代数式表示).23. 问题背景:
(1)、【尝试初探】在点的运动过程中,与始终保持相似关系,请说明理由.(2)、【深入探究】若 , 随着点位置的变化,点的位置随之发生变化,当是线段中点时,求的值.(3)、【拓展延伸】连接 , , 当是以为腰的等腰三角形时,求的值(用含的代数式表示).23. 问题背景: (1)、如图1,正方形ABCD,点E、F分别在边AB、BC上,连接AF与DE交于点O,有∠FOD=90°,则= , 若E为AB中点,则;(2)、尝试应用:
(1)、如图1,正方形ABCD,点E、F分别在边AB、BC上,连接AF与DE交于点O,有∠FOD=90°,则= , 若E为AB中点,则;(2)、尝试应用:如图2,平行四边形ABCD,AB=5,BC=4,点E边AB上,点F在边BC的延长线上,连接AF与DE交于点O,当∠FOD=∠B时,求的值;
(3)、类比拓展:如图3,菱形ABCD中,(m>2),点E在边AB上,点F是BC延长线上一点,且满足 , 连接AF与DE交于点O时,∠DAO=∠AED;直接写出cos∠ABF的值.(用含m的式子表示)