【提升卷】 5.2 平行线同步练习（2023-2024学年华师大版数学七年级上册）

试卷更新日期：2023-09-15 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，下列能判定 $A B$ ∥ $C D$ 的条件有几个（）

(1)、 $∠ 1 = ∠ 2$ （2） $∠ 3 = ∠ 4$ （3） $∠ B = ∠ 5$ （4） $∠ B + ∠ B C D = 180 °$ .

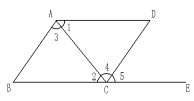A、4 B、3 C、2 D、1

查看试题解析
2. 下列图形中，根据 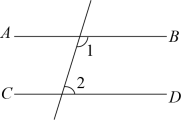$A B ∥ C D$ ，能得到 $∠ 1 = ∠ 2$ 的是（）

A、 B、 C、 D、

查看试题解析
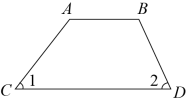3. 如图，两条平行线a，b被第三条直线c所截．若 $∠ 2 = 56 °$ ，则 $∠ 1$ 的度数为（）

A、 $120 °$ B、 $112 °$ C、 $124 °$ D、 $56 °$

查看试题解析
4. 如图， $A B ∥ C D$ ， $∠ F G B ＝ 155 °$ ， $F G$ 平分 $∠ E F D$ ，则 $∠ B E F$ 的大小为（）

A、 $100 °$ B、 $110 °$ C、 $120 °$ D、 $130 °$

查看试题解析
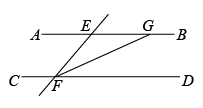5. 如图，下列判断中正确的是（）

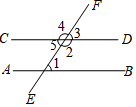A、如果 $∠ 3 + ∠ 2 = 180 °$ ，那么 $A B / / C D$ B、如果 $∠ 1 + ∠ 3 = 180 °$ ，那么 $A B / / C D$ C、如果 $∠ 2 = ∠ 4$ ，那么 $A B / / C D$ D、如果 $∠ 1 = ∠ 5$ ，那么 $A B / / C D$

查看试题解析
6. 如图所示，给出下列条件：①∠1＝∠B；②∠EFD＋∠B＝180°；③∠B＝∠D；④∠E＝∠B；⑤∠BFD＝∠B．其中，一定能判断AB∥CD的条件的个数为（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
7. 如图所示，不能推出AD∥BC的是（）

A、∠DAB+∠ABC=180° B、∠2=∠4 C、∠1=∠3 D、∠CBE=∠DAE

查看试题解析
8. 如图，已知直线AD∥BC，BE平分∠ABC交直线DA于点E，若∠DAB＝54°，则∠E等于（）

A、25° B、27° C、29° D、45°

查看试题解析
9. 把三角板 $A B C$ 按如图所示的位置放置，已知 $∠ C A B = 30 °$ ， $∠ C = 90 °$ ，过三角板的顶点 $A$ 、 $B$ 分别作直线 $A D$ 、 $B E$ ，且 $A D // B E$ ， $∠ D A E = 120 °$ .给出以下结论：
（1） $∠ 1 + ∠ 2 = 90 °$ ；（2） $∠ 2 = ∠ E A B$ ；（3） $C A$ 平分 $∠ D A B$ .其中正确结论有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
10. 为了检验一条纸带的两条边线是否平行，小明沿 $A B$ 折叠后，如图，测量得到：① $∠ 1 = ∠ 4$ ；② $B C = B A$ ；③ $C A = C B$ ；④ $∠ 3 = ∠ 4$ ．其中能够判定两条边线 $E F$ 、 $G H$ 互相平行的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 如图，已知 $A B ∥ C D$ ， $∠ 1 = ∠ 2$ ， $∠ E = 50 °$ ，则 $∠ F$ 的度数．

查看试题解析
12. 如图，在四边形 $A B C D$ 中， $∠ D A C = ∠ A C B$ ， $∠ D = 86 °$ ，则 $∠ B C D =$ 度.

查看试题解析
13. 下列说法中：①在同一平面内，不相交的两条直线叫做平行线；②经过三点一定能画出三条直线；③如果两个角相等，那么这两个角是对顶角；④点C是直线 $A B$ 上的点，如果 $A C = \frac{1}{2} A B$ ，则点C为 $A B$ 的中点.其中正确的有.（填序号）

查看试题解析
14. 在同一平面内， $∠ A$ 与 $∠ B$ 的两边一边平行，另一边垂直，且 $∠ A$ 比 $∠ B$ 的3倍少10°.则 $∠ B$ .

查看试题解析
15. 生活中常见一种折叠拦道闸，如图1所示.若想求解某些特殊状态下的角度，需将其抽象为几何图形，如图2所示，BA垂直于地面AE于A，CD平行于地面AE，则∠ABC+∠BCD＝°.

查看试题解析

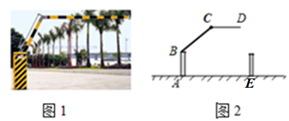
三、综合题

16. 如图，已知 $A B ∥ C D$ ， $∠ B A E = 30 °$ ， $∠ D C E = 60 °$ ， $E F 、 E G$ 三等分 $∠ A E C$ （即 $∠ A E F = ∠ F E G = ∠ G E C$ ）.

(1)、求 $∠ A E F$ 的度数；

(2)、 $E F ∥ A B$ 吗？为什么？

查看试题解析
17. 综合与实践
问题情境：
数学活动课上，老师展示了一个问题：如图1，直线 $l_{1} ∥ l_{2}$ ，直线 $l_{3}$ 与 $l_{1}$ ， $l_{2}$ 分别交于点C，D，点A在直线 $l_{1}$ 上，且在点C的左侧，点B在直线 $l_{2}$ 上，且在点D的左侧，点Р是直线 $l_{3}$ 上的一个动点（点Р不与点C，D重合）．当点Р在点C，D之间运动时，试猜想 $∠ P A C$ ， $∠ A P B$ ， $∠ P B D$ 之间的数量关系，并说明理由．
独立思考：

(1)、请解答老师提出的问题．实践探究：
勤学小组对此问题进行了更深一步的思考：当点Р在C，D两点的外侧运动时， $∠ P A C$ ， $∠ A P B$ ， $∠ P B D$ 之间的数量关系又是如何？

(2)、如图2，当点P运动到点C上方时，试猜想 $∠ P A C$ ， $∠ A P B$ ， $∠ P B D$ 之间的数量关系，并说明理由．

(3)、如图3，当点P运动到点D下方时，请直接写出 $∠ P A C$ ， $∠ A P B$ ， $∠ P B D$ 之间的数量关系．

查看试题解析
18. 如图， $A B ∥ C D$ ，点E为两直线之间的一点

(1)、如图1，若 $∠ B A E = 35 °$ ， $∠ D C E = 20 °$ ，则 $∠ A E C =$ ；

(2)、如图2，试说明， $∠ B A E + ∠ A E C + ∠ E C D = 360 °$ ；

(3)、①如图3，若 $∠ B A E$ 的平分线与 $∠ D C E$ 的平分线相交于点F，判断 $∠ A E C$ 与 $∠ A F C$ 的数量关系，并说明理由；
②如图4，若设 $∠ E = m$ ， $∠ B A F = \frac{1}{n} ∠ F A E$ ， $∠ D C F = \frac{1}{n} ∠ F C E$ ，请直接用含 $m$ 、 $n$ 的代数式表示 $∠ F$ 的度数.

查看试题解析

19. 【教材呈现】下图是华师版七年级上册数学教材第176页的部分内容．

有了“两直线平行，同位角相等”，我们就能用推理的方法得出“两条平行线被第三条直线所截，内错角相等”．

如图5.2.13，平行线a、b被直线l所截，我们将∠1的对顶角记为∠3…

(1)、小明根据提示，写出了如下证明过程．根据小明的推理过程，在括号内填写理由．

∵ $a ∥ b$ ，

∴ $∠ 2 = ∠ 3$ （）．

∵ $∠ 1 = ∠ 3$ （），

∴ $∠ 1 = ∠ 2$ （）．

(2)、如图①，

a ∥ b

．若

∠ 1 = 65 °

，则∠2的余角的大小为度．

(3)、如图②，

A B ∥ C D

，

B C ∥ D E

，若

∠ B = 47 °

，求∠D的大小．

查看试题解析

20. 将一副三角板中的两块直角三角尺的直角顶点C按如图1方式叠放在一起，其中 $∠ A = 60 °$ ， $∠ D = 30 ° ， ∠ E = ∠ B = 45 °$ ．

(1)、若 $∠ l = 25 °$ ，则 $∠ 2$ 的度数为；

(2)、直接写出 $∠ 1$ 与 $∠ 3$ 的数量关系：；

(3)、直接写出 $∠ 2$ 与 $∠ A C B$ 的数量关系：；

(4)、如图2，当 $∠ A C E < 180 °$ 且点E在直线 $A C$ 的上方时，将三角尺 $A C D$ 固定不动，改变三角尺 $B C E$ 的位置，但始终保持两个三角尺的顶点C重合，这两块三角尺是否存在一组边互相平行？请直接写出 $∠ A C E$ 角度所有可能的值 ▲ ．

查看试题解析

【提升卷】 5.2 平行线 同步练习（2023-2024学年华师大版数学七年级上册）

一、选择题

二、填空题

三、综合题

【提升卷】 5.2 平行线同步练习（2023-2024学年华师大版数学七年级上册）