【基础卷】 5.2 平行线 同步练习（2023-2024学年华师大版数学七年级上册）
试卷更新日期：2023-09-15 类型：同步测试
一、选择题
-
1. 直线、、中， ， ， 则直线与直线的关系是（ ）.A、相交 B、平行 C、垂直 D、不能确定2. 如图，已知∥ ， ， 平分 ， 则的度数为（ ）
A、 B、 C、 D、3. 如图，如果、 ， 若 ， 则的和是（ ）
A、 B、 C、 D、4. 如图， ， ， ， 则的大小是（ ）．
A、 B、 C、 D、5. 如图，下列条件中，① ；② ；③ ；④ ，能判断直线 的有（ ）
A、1个 B、2个 C、3个 D、4个6. 如图，若直线 ，则下列各式成立的是（ ）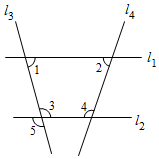
A、 B、 C、 D、7. 如图，已知 ，则下列结论中正确的是（ ）
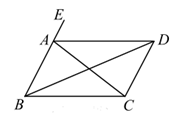A、 B、 C、 D、8. 如图，如果AB∥EF，EF∥CD，下列各式正确的是（ ）
A、∠1+∠2−∠3=90° B、∠1−∠2+∠3=90° C、∠1+∠2+∠3=90° D、∠2+∠3−∠1=180°9. 下列说法：①两点之间，直线最短； ②若AC＝BC，则点C是线段AB的中点；③过一点有且只有一条直线与已知直线垂直； ④过一点有且只有一条直线与已知直线平行．其中正确的说法有（ ）
A、1个 B、2个 C、3个 D、4个10. 下列条件中不能判定AB∥CD的是( )
A、∠1＝∠4 B、∠2＝∠3 C、∠5＝∠B D、∠BAD+∠D＝180°二、填空题
-
11. 如图，内有一点 ， 过点画 ， ， ， 则的度数为度．
12. 如图， ， ， ， 则等于度．
13. 如图，给出下列条件：① ；② ；③ ；④ ；⑤ .其中，一定能判定 ∥ 的条件有（填写所有正确的序号）.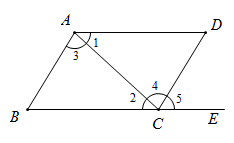
14. 如图所示，C岛在A岛的北偏东50°方向，C岛在B岛的北偏西40°方向，则从C岛看A、B两岛的视角∠ACB等于.
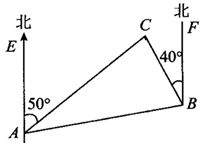15. 如图，直线CE∥DF，∠CAB＝120°，∠ABD＝80°，则∠ECA+∠BDF＝ ．
三、解答题
-
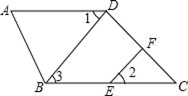
16. 如图，填空并填写理由：
因为∠1=∠2，所以AD∥BC（ ）．
因为∠A+∠ABC=180°，所以AD∥BC（ ）．
因为（ ）∥（ ），所以∠C+∠ABC=180°(两直线平行，同旁内角互补)
因为（ ）∥（ ），所以∠3=∠C(两直线平行，同位角相等)．
17. 已知：如图，BE∥GF ， ∠1＝∠3，∠DBC＝70°，求∠EDB的大小．阅读下面的解答过程，并填空(理由或数学式)
解：∵BE∥GF(已知)
∴∠2＝∠3.
∵∠1＝∠3.
∴∠1＝ ， .
∴DE∥ ， .
∴∠EDB+∠DBC＝180°.
∴∠EDB＝180°﹣∠DBC(等式性质)
∵∠DBC＝.(已知)
∴∠EDB＝180°﹣70°＝110°
18. 完成下面的证明：如图，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，连接DE，DF，DE∥AB，∠BFD＝∠CED，连接BE交DF于点G，求证：∠EGF+∠AEG＝180°．证明：∵DE∥AB（已知），
∴∠A＝∠CED
又∵∠BFD＝∠CED（已知），
∴∠A＝∠BFD
∴DF∥AE
∴∠EGF+∠AEG＝180°
