【提升卷】5.1 相交线 同步练习（2023-2024学年华师大版数学七年级上册）
试卷更新日期：2023-09-15 类型：同步测试
一、选择题
-
1. 如图，已知直线、相交于点O，平分 ， 若 ， 则度数是（ ）
A、65° B、50° C、25° D、130°2. 下列四个说法：①两点确定一条直线；②过直线上一点有且只有一条直线垂直于已知直线；③连接直线外一点与直线上各点的所有线段中，垂线段最短；④从直线外一点到这条直线的垂线段，叫做点到直线的距离，其中正确的说法的个数是（ ）A、1 B、2 C、3 D、43. 如图，点P在直线外， ， ， 则线段的值可能为（ ）
A、1 B、2 C、3 D、44. 如图，点P是直线l外一点，从点P向直线l引PA，PB，PC，PD（点A，B，C，D在直线l上）4条线段，其中于点C．这4条线段中，长度最短的是（ ）
A、PA B、PB C、PC D、PD5. 如图，点A是直线l外一点，过点A作于点B．在直线l上取一点C，连接 ， 使 ， 点P在线段上，连接 ， 若 ， 则线段的长不可能是（ ）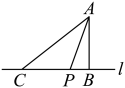
A、3.5 B、4.1 C、5 D、5.56. 如图所示， ，垂足分别为A、D，已知 ，则点A到线段 的距离是（ ）
A、10 B、8 C、6 D、4.87. 如图，已知直线AB与CD相交于点O，OE平分∠AOD，∠EOF＝90°.对于下列结论：①∠BOC＝2∠AOE；②OF平分∠BOD；③∠AOE是∠BOF的余角；④∠AOE是∠COE的补角.其中正确结论的个数是（ ）
A、1 B、2 C、3 D、48. 如图，表示点A到BC距离的是（ ）
A、AD的长度 B、AE的长度 C、BE的长度 D、CE的长度9. 如图，直线AB、CD相交于点O，
，OF平分∠AOE，∠1=15°30′，则下列结论中，错误的是（ ） 
A、∠2=45° B、∠1=∠3 C、∠AOD与∠1互为补角 D、∠1的余角等于75°30′10. 如图，已知直线AB和CD相交于点O，于点O，图中∠1与∠2的关系是（ ）
A、 B、 C、 D、无法确定二、填空题
-
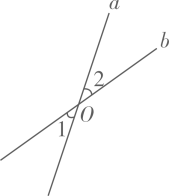
11. 如图，直线a、b交于点O，若 ， 则 ．
12. 如图，直线AB，CD交于点O，∠AOC：∠COE=1：2．若∠BOD=28°，则∠COE等于度．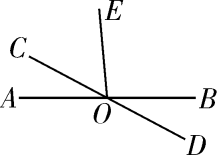
13. 如图，运动会上，小明自踏板M处跳到沙坑P处，甲、乙、丙三名同学分别测得PM＝3.25米，PN＝3.15米，PF＝3.21米，则小明的成绩为 米．（填具体数值）
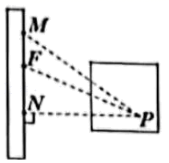14. 如图，直线AB与CD相交于点O ， ，若 ，则 =°．
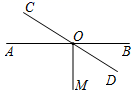15. 如图， ， ，已知 ， ， ，则点 到直线 的距离是 ．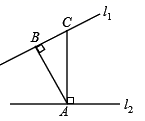
三、综合题
-
16. 如图，点C在射线上，于点F．
(1)、使用圆规和直尺作图：（要求：保留作图痕迹，不写作法）在射线上画出点E，使C为线段的中点，连接 ．
(2)、连接 ， 在线段 ， ， 中，线段最短，依据是 ．(3)、若 ， 求的度数．17. 如图，直线AE与CD相交于点B，BF⊥AE．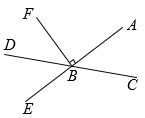
(1)、若∠DBE＝60°，求∠FBD的度数；(2)、猜想∠CBE与∠DBF的数量关系，并说明理由．18. 如图，已知直线BC及直线外一点A，按要求完成下列问题：
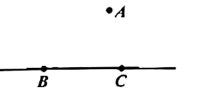(1)、画出射线CA，线段AB，过C点画CD⊥AB，垂足为点D；(2)、比较线段CD和线段CA的大小，并说明理由.19. 如图， 是平面内三点.
(1)、按要求作图：请先用铅笔作图，确认无误后，再用黑色水笔描深.①作射线 ，过点 作直线 ，使 两点在直线 两旁；
②过点 作直线 的垂线段，垂足为 ；
③点 为直线 上任意一点，点 为射线 上任意一点，连结线段 .
(2)、在（1）所作图形中，若点 到直线 的距离为2，点 到射线 的距离为5，点 、 之间的距离为8，点 之间的距离为6，则 的最小值为 ， 依据是.20. 已知点直线BC及直线外一点A(如图），按要求完成下列问题：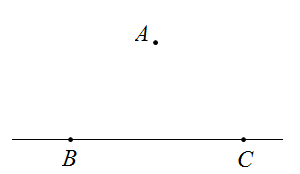
(1)、画出射线CA、线段AB.过C点画CD⊥AB，垂足为点D；(2)、比较线段CD和线段CA的大小，并说明理由；(3)、在以上的图中，互余的角为 ， 互补的角为.（各写出一对即可）