【提升卷】 4.5 最基本的图形——点和线 同步练习（2023-2024学年华师大版数学七年级上册）
试卷更新日期：2023-09-15 类型：同步测试
一、选择题
-
1. 如图，已知线段cm，C为直线上一点，且cm，M，N分别是、的中点，则等于（ ）cm.
A、13 B、12 C、10或8 D、102. 如图，线段上依次有D，B，E三点，其中点B为线段的中点， ， 若 ， 则等于（ ）
A、4 B、4.5 C、5 D、63. 如图，D是AB的中点，E是BC的中点，若AD=6，BC=8，则下列说法中错误的是（ ）
A、AC=20 B、DC=16 C、DE=10 D、BE=44. 如图，数轴上点M，P，N分别表示数m，m+n，n，那么原点的位置是（ ）
A、在线段MP上 B、在线段PN上 C、在点M的左侧 D、在点N的右侧5. 在下列生活、生产现象中，可以用基本事实“两点之间，线段最短”来解释的是（ ）①用两颗钉子就可以把木条固定在墙上；②在A、B两地之间架设电线时，总是尽可能沿线段AB架设；③植树时，只要栽下两棵树，就可以把同一行树栽在同一条直线上；④把弯曲的公路改直，就能缩短路程.
A、①② B、①③ C、②④ D、③④6. 如图，C、D是线段AB上的两点，且D是线段AC的中点，AB=10cm，BC＝4cm，则AD的长为（ ）
A、2cm B、3cm C、4cm D、6cm7. 平面上有三点 ， 如果 ， ， ， 那么（ ）A、点在线段上 B、点在线段的延长线上 C、点在直线外 D、点可能在直线上，也可能在直线外8. 如图，点C为线段的中点，点D在线段上，如果 ， ， 那么线段的长是（ ）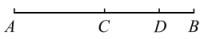
A、2 B、3 C、4 D、59. 如图，C，D是线段AB上的两点，E是AC的中点，F是BD的中点，若EF＝m，CD＝n，则AB＝（ ）
A、m-n B、m+n C、2m-n D、2m+n10. 如图，线段AB＝16cm，在AB上取一点C，M是AB的中点，N是AC中点，若MN＝3cm，则线段AC的长是（ ）
A、6 B、8 C、10 D、12二、填空题
-
11. A、B、C三点在同一条直线上，AB=6cm，BC=2cm，则AC=.12. 已知线段AB＝16，AM＝BM，点P、Q分别是AM、AB的中点，当点M在直线AB上时，则PQ的长为.13. 同一条直线上有三点 ， ， 且线段 ， 点是的中点，厘米，则线段的长为.14. 如图，点C在线段AB上，且AC：BC＝2：3，点D在线段AB的延长线上，且BD＝AC，E为AD的中点，若AB＝40cm，则线段CE＝.
15. 如图，点是线段上一点， ， 点是线段的中点，点是线段的中点， ， ， 则线段的长度为.
三、综合题
-
16. 同学们，我们都知道：表示与的差的绝对值，实际上也可理解为与两数在数轴上所对应的两点之间的距离；表示与的差的绝对值，实际上也可理解为与两数在数轴上所对应的两点之间的距离，试探索：(1)、（）；（）；(2)、写出使得成立的所有整数；(3)、若数轴上表示数a的点位于与之间，求的值.17. 如图，C为线段上一点，点B为的中点，且.
(1)、图中共有条线段.(2)、求的长.(3)、若点E在直线上，且 ， 求BE的长.18. 如图，线段的中点O是数轴原点，点C在点O右侧，分线段的长度为 ， 且.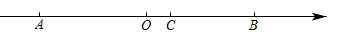
(1)、求点A在数轴上代表的数是什么？请说明理由.(2)、若点P从点C出发，以3个单位/秒的速度向点A运动，到点A停止；点Q从点O出发，以1个单位/秒速度向点B运动，到点B后停止.问运动时间t为几秒时，？
