2023-2024学年高中数学人教A版必修二 6.3 平面向量基本定理及坐标表示同步练习

试卷更新日期：2023-09-12 类型：同步测试

进入出卷网下载

一、选择题

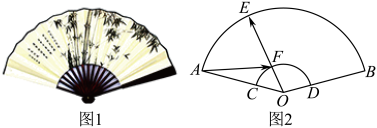
1. 已知 $| \vec{a} | = 1$ ， $| \vec{b} | = 2$ ， $| 2 \vec{a} - \vec{b} | = 4$ ，则 $\vec{a}$ 与 $\vec{b}$ 夹角的余弦值为（）

A、－1 B、 $- \frac{1}{2}$ C、0 D、1

查看试题解析
2. 已知向量 $\vec{a}$ 、 $\vec{b}$ ， “ $| \vec{a} | = | \vec{b} |$ ”是“ $\vec{a}$ 在 $\vec{b}$ 方向上的数量投影与 $\vec{b}$ 在 $\vec{a}$ 方向上的数量投影相等”的（）

A、充分非必要条件 B、必要非充分条件 C、充要条件 D、既非充分又非必要条件

查看试题解析
3. 已知向量 $\vec{a} = (3 ， 1) ， \vec{b} = (- 2 ， m)$ ，且 $\vec{a} / / \vec{b}$ ，则实数 $m$ 的值为（）

A、 $- \frac{3}{2}$ B、 $\frac{3}{2}$ C、 $- \frac{2}{3}$ D、 $\frac{2}{3}$

查看试题解析
4. 已知向量 $\vec{a} = (2 ， 3)$ ， $\vec{b} = (- 1 ， - 2)$ ，则 $2 \vec{a} - \vec{b} =$ （）

A、 $(3 ， 5)$ B、 $(- 5 ， - 7)$ C、 $(5 ， 8)$ D、 $(3 ， 4)$

查看试题解析
5. 已知向量 $\vec{a} = (1 ， m)$ ， $\vec{b} = (2 ， - 1)$ ，且 $\vec{a} ∥ \vec{b}$ ，则实数 $m =$ （）

A、-2 B、 $- \frac{1}{2}$ C、 $\frac{1}{2}$ D、2

查看试题解析
6. 已知向量 $\vec{a} = (2 ， 2)$ ， $\vec{b} = (1 ， - 1)$ ，则（）

A、 $\vec{a} = - 2 \vec{b}$ B、 $\vec{a} = 2 \vec{b}$ C、 $\vec{a} / / \vec{b}$ D、 $\vec{a} ⊥ \vec{b}$

查看试题解析
7. 已知 $\vec{a}$ ， $\vec{b}$ 是单位向量， $| 2 \vec{a} + \vec{b} | = \sqrt{3}$ ，则 $\vec{a}$ 与 $\vec{b}$ 的夹角为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{2 π}{3}$ D、 $\frac{5 π}{6}$

查看试题解析
8. 在 $▱ A B C D$ 中， $G$ 为 $△ A B C$ 的重心，满足 $\vec{A G} = x \vec{A B} + y \vec{A D} (x ， y \in R)$ ，则 $x + 2 y =$ （）

A、 $\frac{4}{3}$ B、 $\frac{5}{3}$ C、0 D、-1

查看试题解析
9. 折扇又名“纸扇”是一种用竹木或象牙做扇骨、韧纸或者绫绢做扇面的能折叠的扇子.某折扇如图1所示，其平面图为如图2所示的扇形AOB ，其半径为3， $∠ A O B = 150 °$ ，点E ， F分别在 $\overset{⌢}{A B}$ ， $\overset{⌢}{C D}$ 上，且 $\vec{F E} = 2 \vec{O F}$ ，则 $\vec{A F} \cdot \vec{O E}$ 的取值范围是（）

A、 $[- 6 ， \frac{15}{2}]$ B、 $[3 - \frac{9 \sqrt{3}}{2} ， 6]$ C、 $[- \frac{3}{2} ， 3 + \frac{9 \sqrt{3}}{2}]$ D、 $[- 6 ， 3 + \frac{9 \sqrt{3}}{2}]$

查看试题解析
10. 已知点P在 $△ A B C$ 所在平面内，满足 $\vec{P A} + \vec{P B} + \vec{P C} = \vec{0}$ ，且 $\vec{A B} = m \vec{A P} + n \vec{A C}$ ，则 $m + n =$ （）

A、 $\frac{2}{3}$ B、1 C、 $\frac{4}{3}$ D、2

查看试题解析
11. 如图，在 $△ A O D$ 中， $| \vec{O A} | > | \vec{O D} |$ ， $B ， C$ 分别在 $A D$ 上，且 $A B = B C = C D$ ，点 $P$ 为 $A D$ 的中点，则下列各值中最小的为（）

A、 $\vec{O P} \cdot \vec{O A}$ B、 $\vec{O P} \cdot \vec{O B}$ C、 $\vec{O P} \cdot \vec{O C}$ D、 $\vec{O P} \cdot \vec{O D}$

查看试题解析

二、多项选择题

12. 已知单位向量 $\vec{a}$ ， $\vec{b}$ 满足 $| 2 \vec{a} - \vec{b} | = \sqrt{3}$ ，则以下结论正确的有（）

A、 $\vec{a} \cdot \vec{b} = \frac{1}{2}$ B、 $\vec{a} ⊥ (\vec{a} - \vec{b})$ C、向量 $\vec{a}$ ， $\vec{b}$ 的夹角为 $30 °$ D、 $\vec{b}$ 在 $\vec{a}$ 上的投影向量为 $\frac{1}{2} \vec{a}$

查看试题解析
13. 在平面直角坐标系中，已知 $\vec{a} = (c o s α ， s i n α)$ ， $\vec{b} = (c o s β ， 2 c o s β)$ ，则下列结论正确的是（）

A、 $| \vec{b} |$ 的取值范围是 $[0 ， \sqrt{5}]$ B、当 $\vec{b} \neq \vec{0}$ 时， $\vec{a}$ 在 $\vec{b}$ 方向上的投影数量的取值范围是 $[0 ， 1]$ C、 $| 2 \vec{a} - \vec{b} |$ 的最大值是 $2 + \sqrt{5}$ D、若 $\vec{c} = x \vec{a} + y \vec{b}$ ，且 $x^{2} + 5 y^{2} = 2$ ，则 $| \vec{c} |$ 最大值为2

查看试题解析
14. 下列说法正确的是（）

A、对任意向量 $\vec{a}$ ， $\vec{b}$ ，都有 $| \vec{a} \cdot \vec{b} | \leq | \vec{a} | | \vec{b} |$ B、对任意非零向量 $\vec{a}$ ， $\vec{b}$ ，都有 $| \vec{a} + \vec{b} | < | \vec{a} | + | \vec{b} |$ C、若向量 $\vec{a}$ ， $\vec{b}$ 满足 $(\vec{a} + \vec{b}) ⊥ (\vec{a} - \vec{b})$ ，则 $| \vec{a} | = | \vec{b} |$ D、若非零向量 $\vec{a}$ ， $\vec{b}$ 满足 $\vec{a} ⊥ \vec{b}$ ，则 $| \vec{a} + \vec{b} | = | | \vec{a} | - | \vec{b} | |$

查看试题解析
15. 下列说法正确的是（）

A、若 $\vec{a} / / \vec{b}$ ， $\vec{b} / / \vec{c}$ ，则 $\vec{a} / / \vec{c}$ B、 $| (\vec{a} \cdot \vec{b}) \cdot \vec{c} | \leq | \vec{a} | | \vec{b} | | \vec{c} |$ C、若 $\vec{a} ⊥ (\vec{b} - \vec{c})$ ，则 $\vec{a} \cdot \vec{b} = \vec{a} \cdot \vec{c}$ D、 $(\vec{a} \cdot \vec{b}) \cdot \vec{b} = \vec{a} \cdot {(\vec{b})}^{2}$

查看试题解析
16. 如图，在平行四边形ABCD中， $∠ B = 60 °$ ， $B C = 2 A B = 2$ ，点E是边AD上的动点（包含端点），则下列结论正确的是（）

A、当点E是AD的中点时， $\vec{B D} = \vec{B E} + \frac{1}{2} \vec{B C}$ B、存在点 $E$ ，使得 $(\vec{B A} - \frac{1}{2} \vec{B C}) ⊥ \vec{C E}$ C、 $\vec{E B} \cdot \vec{E C}$ 的最小值为 $- \frac{1}{4}$ D、若 $\vec{C E} = x \vec{C B} + y \vec{C D}$ ， $x ， y \in R$ ，则 $x + 2 y$ 的取值范围是 $[2 ， 3]$

查看试题解析

三、填空题

17. 如果平面向量 $\vec{a} = (1 ， - 2) ， \vec{b} = (- 6 ， 3)$ ，那么向量 $\vec{a} + \vec{b}$ 在 $\vec{a}$ 上的投影向量为.

查看试题解析
18. 已知平面向量 $\vec{a} = (3 ， 1)$ ， $\vec{b} = (- 1 ， 1)$ ， $\vec{c} = (x ， - 6)$ .若 $(\vec{a} + 2 \vec{b}) / / \vec{c}$ ，则x＝.

查看试题解析
19. 已知 $\vec{a} = (2 ， - 3)$ ， $\vec{b} = (0 ， k)$ ， $\vec{a}$ 与 $2 \vec{a} + \vec{b}$ 平行，则实数 $k$ 的值为.

查看试题解析
20. 已知向量 $\vec{a}$ ， $\vec{b}$ 满足 $| \vec{a} | = 2 | \vec{b} | = 2$ ， $\vec{a} \cdot \vec{b} = 1$ ，则 $| 2 \vec{a} - \vec{b} | =$ .

查看试题解析
21. 已知平面向量 $\vec{a}$ ， $\vec{b}$ ， $| \vec{a} | = 1$ ， $\vec{b} = (1 ， - 1)$ ， $\vec{a} ⊥ (\vec{a} - \vec{b})$ ，则 $| \vec{a} + 2 \vec{b} |$ 的值是.

查看试题解析
22. 已知向量 $\vec{a}$ ， $\vec{b}$ 的夹角为 $\frac{π}{3}$ ， $\vec{a} = (2 ， 0)$ ，则 $\vec{a}$ 在 $\vec{b}$ 方向上的数量投影为.

查看试题解析

四、解答题

23. 在矩形 $A B C D$ 中， $A B = 2$ ， $A D = 1$ ，点 $M$ 、 $N$ 分别是边 $B C$ 、 $C D$ 的中点，设向量 $\vec{A B} = \vec{a}$ ， $\vec{A D} = \vec{b}$

(1)、试用 $\vec{a} 、 \vec{b}$ 表示向量 $\vec{A M}$ 与 $\vec{A N}$ ；

(2)、求 $\vec{A M} \cdot \vec{A N}$ 的值.

查看试题解析
24. 已知 $\vec{a} = (m ， 2)$ ， $\vec{b} = (- 2 ， 1)$ ， $\vec{c} = (3 ， 2)$ .

(1)、若 $\vec{a} ∥ (\vec{b} + 2 \vec{c})$ ，求实数 $m$ 的值；

(2)、若 $(\vec{a} - \vec{b}) ⊥ (\vec{b} + \vec{c})$ ，求实数 $m$ 的值.

查看试题解析
25. 如图，已知 $A B C D$ 为平行四边形．

(1)、若 $| \vec{A B} | = 5$ ， $| \vec{A D} | = 4$ ， $| \vec{B D} | = \sqrt{21}$ ，求 $\vec{A B} \cdot \vec{A D}$ 及 $| \vec{A C} |$ 的值；

(2)、记平行四边形 $A B C D$ 的面积为 $S$ ，设 $\vec{A B} = (x_{1} ， y_{1})$ ， $\vec{A D} = (x_{2} ， y_{2})$ ，求证： $S = | x_{1} y_{2} - x_{2} y_{1} |$

查看试题解析
26. 已知平面向量 $\vec{a} ， \vec{b} ， | \vec{a} | = 2 ， | \vec{b} | = \sqrt{3}$ ，且 $\vec{b} \cdot (\vec{a} - \vec{b}) = 0$ .

(1)、求 $\vec{a}$ 与 $\vec{b}$ 的夹角 $θ$ 的值；

(2)、当 $| \vec{b} - λ \vec{a} |$ 取得最小值时，求实数 $λ$ 的值.

查看试题解析
27. 已知 $\vec{a}$ ， $\vec{b}$ 是非零向量，① $| \vec{a} | = \sqrt{3} | \vec{b} |$ ；② $〈 \vec{a} ， \vec{b} 〉 = \frac{π}{6}$ ；③ $| \vec{a} - \vec{b} | = | \vec{b} |$ .

(1)、从①②③中选取其中两个作为条件，证明另外一个成立；（注：若选择不同的组合分别解答，则按第一个解答计分.）

(2)、在①②的条件下， $(\vec{a} + \vec{b}) ⊥ (\vec{a} - λ \vec{b})$ ，求实数 $λ$ .

查看试题解析
28. 记 $\vec{a}$ 、 $\vec{b}$ 、 $\vec{c}$ 为平面单位向量，且 $| \vec{a} - \vec{b} | = 1$ .

(1)、求 $⟨ \vec{a} ， \vec{b} ⟩$ ；

(2)、若 $\vec{a} \cdot \vec{c} = \frac{1}{2}$ ，求 $| 2 \vec{c} - \vec{a} |$ .

查看试题解析
29. 已知 $\vec{e_{1}} ， \vec{e_{2}}$ 是夹角为 $6 0^{∘}$ 的单位向量， $\vec{a} = 2 \vec{e_{1}} - \vec{e_{2}} ， \vec{b} = \vec{e_{1}} + 3 \vec{e_{2}}$ .

(1)、若 $\vec{a} + λ \vec{b}$ 与 $\vec{b}$ 垂直，求实数 $λ$ 的值；

(2)、若 $\vec{c} = x \vec{a} + y \vec{b} (x ， y \in R$ ，且 $y \neq 0)$ ，求 $\frac{| \vec{c} |}{| y |}$ 的最小值.

查看试题解析
30. 设平面向量 $\vec{a}$ 、 $\vec{b}$ 的夹角为 $θ$ ， $\vec{a} \otimes \vec{b} = | \vec{a} | \cdot | \vec{b} | s i n θ$ ．已知 $\vec{a} = (s i n x ， 1)$ ， $\vec{b} = (c o s x ， 1)$ ， $f (x) = \vec{a} \otimes \vec{b} (0 \leq x < \frac{3 π}{4})$ ．

(1)、求 $f (x)$ 的解析式；

(2)、若 $f (x) g (x) = - c o s 2 x$ ﹐证明：不等式 $e^{f (x)} + f^{2} (x) + f (x) > 2 + 2 l n g (x)$ 在 $[\frac{π}{2} ， \frac{3 π}{4})$ 上恒成立．

查看试题解析

2023-2024学年高中数学人教A版必修二 6.3 平面向量基本定理及坐标表示 同步练习

一、选择题

二、多项选择题

三、填空题

四、解答题

2023-2024学年高中数学人教A版必修二 6.3 平面向量基本定理及坐标表示同步练习