（单元测试A卷）第四章一次函数—北师大版2023-2024学年八年级数学上册

试卷更新日期：2023-09-12 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列图象中，表示y是x的函数的个数有（）

A、1 B、2个 C、3个 D、4个

查看试题解析
2. 函数y= $\frac{1}{x - 2}$ 中自变量x的取值范围是（）

A、x≠-2 B、x≠2 C、x<2 D、x>2

查看试题解析
3. 下列式子中，表示y是x的正比例函数的是（）

A、 $y = \frac{x}{2}$ B、 $y = \frac{2}{x}$ C、 $y = x^{2}$ D、 $y = \sqrt{x}$

查看试题解析
4. 函数y=(k²-1)x+3是一次函数，则k的取值范围是（）

A、k≠1 B、k≠-1 C、k≠±1 D、k为任意实数

查看试题解析
5. 已知函数y＝（m﹣2） $x^{m^{2} - 3}$ ＋1是一次函数，则m的值为（）

A、± $\sqrt{3}$ B、 $\sqrt{3}$ C、±2 D、﹣2

查看试题解析
6. 若一次函数y＝(m－3)x－4的图象经过点A(x₁ ， y₁)和点B(x₂ ， y₂)，当x₁>x₂时，y₁>y₂ ，则m的取值范围是（）

A、m<3 B、m>3 C、m≤3 D、m≥3

查看试题解析
7. 在平面直角坐标系中，将直线l₁： $y = - 2 x - 2$ 平移后得到直线l₂： $y = - 2 x + 4$ ，则下列平移作法中，正确的是（）

A、将直线l₁向上平移6个单位 B、将直线l₁向上平移3个单位 C、将直线l₁向上平移2个单位 D、将直线l₁向上平移4个单位

查看试题解析
8. 已知 $(- 2 ， y_{1}) ， (- 1 ， y_{2}) ， (1 ， y_{3})$ 都在直线 $y = - x + 2$ 上，则 $y_{1} ， y_{2} ， y_{3}$ 的值的大小关系是（）

A、 $y_{1} > y_{3} > y_{2}$ B、 $y_{1} < y_{2} < y_{3}$ C、 $y_{3} > y_{1} > y_{2}$ D、 $y_{1} > y_{2} > y_{3}$

查看试题解析
9. 如图，一次函数y＝ $\frac{3}{2}$ x的图象与y＝kx＋7的图象相交于点A，则方程组 ${\begin{array}{l} y = k x + 7 \\ y = \frac{3}{2} x \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$ B、 ${\begin{array}{l} x = 3 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$ D、 ${\begin{array}{l} x = 3 \\ y = 7 \end{array}$

查看试题解析
10. 已知点A（3，y₁）和点B（﹣2，y₂）是一次函数y＝﹣2x＋3图象上的两点，比较y₁与y₂的大小关系（）

A、y₁＞y₂ B、y₁＝y₂ C、y₁＜y₂ D、不能确定

查看试题解析

二、填空题（每题3分，共15分）

11. 函数 $f (x) = \frac{6}{x - 2}$ ，则 $f (\sqrt{3}) =$ ．

查看试题解析
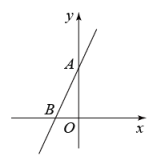
12. 已知函数 $y = 2 x^{m - 1} + 5$ 是一次函数，则 $m$ 的值为.

查看试题解析
13. 已知正比例函数 $y = k x$ 的图象经过第二、四象限，若点 $A (1 ， a) ， B (- 1 ， b)$ 在该函数的图象上，则ab.（填“>”“<”或“=”）

查看试题解析
14. 一次函数y＝（2m-1）x+2的值随x值的增大而增大，则常数m的取值范围为.

查看试题解析
15. 如图，直线AB是一次函数 $y = k x + k - 1$ 的图象，若关于x的方程 $k x + k - 1 = 0$ 的解是 $x = - \frac{2}{3}$ ，则直线AB的函数关系式为．

查看试题解析

三、解答题（共4题，共20分）

16. 已知函数 $y = (m + 2) x^{m^{2} - 3} + m - 2$ 是一次函数，求m的值.

查看试题解析
17. 求经过A（-2 ，-3）和B(-3, 9）两点的直线解析式。

查看试题解析
18. 在平面直角坐标系中，一条直线经过 $A (- 1 ， 5)$ ， $B (a ， - 3)$ ， $C (3 ， 13)$ 三点．求这条直线的解析式并求出a的值．

查看试题解析
19. 在平面直角坐标系中，已知两点坐标 $A (a^{2} - 11 ， - 3)$ ， $B (5 ， 1 - a)$ ，若 $A B$ // $y$ 轴，求一次函数 $y = a x - 4$ 的图像与x轴交点坐标．

查看试题解析

四、综合题（共4题，共35分）

20. 已知等腰三角形的周长为12，设腰长为x，底边长为y.

(1)、试写出y关于x的函数表达式，并直接写出自变量x的取值范围.

(2)、当x=5时，求出函数值.

查看试题解析
21. 已知函数 $y = (m - 1) x + m^{2} - 1$ ．

(1)、当m为何值时，y是x的一次函数？

(2)、当m为何值时，y是x的正比例函数？

查看试题解析
22. 已知y关于x的一次函数 $y = k x + b (k \neq 0)$ ，当 $x = 8$ 时， $y = 12$ ；当 $x = 4$ 时， $y = 4$ .

(1)、求k、b的值；

(2)、若 $A (m ， y_{1})$ ， $B (m + 1 ， y_{2})$ 是该一次函数图象上的两点，求证： $y_{2} - y_{1} = k$ .

查看试题解析
23. 甲、乙两辆汽车分别从A、B两地同时出发，沿同一条公路相向而行，乙车车发2h后休息，与甲车相遇后，继续行驶，设甲、乙两车与B地的路程分别为y_甲（km），y_乙（km），甲车行驶的时间为x（h），y_甲， y_乙与x之间的函数图象如图所示，结合图象解答下列问题：

(1)、求：y_甲与x的函数关系式，并写出自变量x的取值范围；

(2)、乙车休息了h；

(3)、当两车相距80km时，直接写出x的值．

查看试题解析

（单元测试A卷）第四章 一次函数—北师大版2023-2024学年八年级数学上册

一、选择题（每题3分，共30分）

二、填空题（每题3分，共15分）

三、解答题（共4题，共20分）

四、综合题（共4题，共35分）

（单元测试A卷）第四章一次函数—北师大版2023-2024学年八年级数学上册