【提升卷】4.4 平面图形 同步练习(2023-2024学年华师大版数学七年级上册)
试卷更新日期:2023-09-12 类型:同步测试
一、选择题
-
1. 一个圆与一个正方形的周长相等,则圆的面积( )正方形面积。A、相等 B、大于 C、小于 D、无法确定2. 如图,三个大小相同的长方形拼在一起组成一个大长方形,把第二个长方形平均分成2份;再把第3个长方形平均分成3份,那么图中阴影部分是大长方形面积的( )
 A、 B、 C、 D、3. 一个圆的半径为r,圆周长为C1 , 面积为S1;一个半圆的半径为2r,半圆弧长为C2 , 面积为S2 , 那么一下结论成立的是( )A、C1=C2 B、2C1=C2 C、S1=S2 D、S1=2S24. 将一个圆分割成四个大小相同的扇形,则每个扇形的圆心角是( )度.A、45 B、60 C、90 D、1205. 如图所示,则图中三角形的个数一共是( )
A、 B、 C、 D、3. 一个圆的半径为r,圆周长为C1 , 面积为S1;一个半圆的半径为2r,半圆弧长为C2 , 面积为S2 , 那么一下结论成立的是( )A、C1=C2 B、2C1=C2 C、S1=S2 D、S1=2S24. 将一个圆分割成四个大小相同的扇形,则每个扇形的圆心角是( )度.A、45 B、60 C、90 D、1205. 如图所示,则图中三角形的个数一共是( )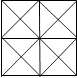 A、16 B、32 C、40 D、446. 一个商标图案如图4中阴影部分,在长方形ABCD中,AB=6cm,BC=4cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则阴影部分的面积是( )
A、16 B、32 C、40 D、446. 一个商标图案如图4中阴影部分,在长方形ABCD中,AB=6cm,BC=4cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则阴影部分的面积是( ) A、(4π+4)cm2 B、(4π+8)cm2 C、(8π+4)cm2 D、(4π﹣16)cm27. 下列四张正方形硬纸片,分别将阴影部分剪去后,再沿虚线折叠,其中可以围成一个封闭长方体包装盒的是( )
A、(4π+4)cm2 B、(4π+8)cm2 C、(8π+4)cm2 D、(4π﹣16)cm27. 下列四张正方形硬纸片,分别将阴影部分剪去后,再沿虚线折叠,其中可以围成一个封闭长方体包装盒的是( )
A、 B、
B、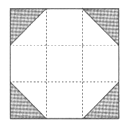 C、
C、 D、
D、 8.
8.如图,按给定的点和边,一共可以数出( )个多边形?
 A、24 B、30 C、36 D、409. 如图,半径为r的小圆在半径为R的大圆内.已知阴影部分面积是小圆面积的3倍.则=( )
A、24 B、30 C、36 D、409. 如图,半径为r的小圆在半径为R的大圆内.已知阴影部分面积是小圆面积的3倍.则=( ) A、 B、 C、 D、10.
A、 B、 C、 D、10.如图所示,平面上5个叠放的圆,它们由上到下的次序应当是( )
 A、X,V,W,Y,Z B、X,Y,W,V,Z C、Y,Z,V,W,X D、V,W,Z,Y,X
A、X,V,W,Y,Z B、X,Y,W,V,Z C、Y,Z,V,W,X D、V,W,Z,Y,X二、填空题
-
11.
如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是 .
 12.
12.如图所示,图中共有 个长方形.
 13. 下列几何图形:圆,圆柱,球,扇形,等腰三角形,长方体,正方体,直角,其中平面图形有 个.14. 将一个圆分割成三个扇形,它们的圆心角的度数比为1:2:3,这三个圆心角中最小的圆心角度数为 .15. 一个圆被分成四个扇形,若各个扇形的面积之比为4:2:1:3,则最小的扇形的圆心角的度数为 .
13. 下列几何图形:圆,圆柱,球,扇形,等腰三角形,长方体,正方体,直角,其中平面图形有 个.14. 将一个圆分割成三个扇形,它们的圆心角的度数比为1:2:3,这三个圆心角中最小的圆心角度数为 .15. 一个圆被分成四个扇形,若各个扇形的面积之比为4:2:1:3,则最小的扇形的圆心角的度数为 .三、综合题
-
16. 【教材呈现】下图是华师版七年级上册数学教材第104页的部分内容

例5如图3.4.1所示的窗框,上半部分为半圆,下半部分为6个大小一样的长方形,长方形的长和宽的比为3:2.
设长方形的长为x米,用x表示所需材料的长度(重合部分忽略不计)
(1)、请根据教材提示,结合图3.4.1,写出例5中第(1)题完整的解题过程(2)、【结论应用】图①、图②是某设计师设计的两种窗户设计图,图①是由边长4a正方形和直径4a半圆组成,图②是由一个八边形和直径2a的圆组成。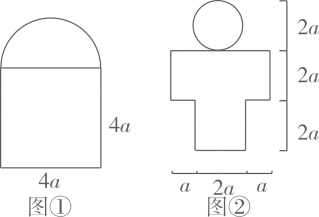
求图②的面积(用含有a的代数式表示,结果保留π).
(3)、用铁丝做成图①、图②,这两个图形用的铁丝的长度是否相同,如果相同,请说明理由,如果不同,请比较出哪个设计图大?17. 如图,OA,OB,OC是圆的三条半径. (1)、若他们的圆心角度数比为1:2:3,求这三个扇形的圆心角的度数.(2)、在(1)的条件下,若圆的半径为2cm,求这三个扇形的面积.(保留π)18. 如图所示,若将类似于a、b、c、d四个图的图形称做平面图,则其顶点数、边数与区域数之间存在某种关系.观察图b和表中对应的数值,探究计数的方法并作答.
(1)、若他们的圆心角度数比为1:2:3,求这三个扇形的圆心角的度数.(2)、在(1)的条件下,若圆的半径为2cm,求这三个扇形的面积.(保留π)18. 如图所示,若将类似于a、b、c、d四个图的图形称做平面图,则其顶点数、边数与区域数之间存在某种关系.观察图b和表中对应的数值,探究计数的方法并作答. (1)、数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:
(1)、数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:图
a
b
c
d
顶点数(S)
7
边数(M)
9
区域数(N)
3
(2)、根据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系;(3)、如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系可知这个平面图有条边.19. 回答下列问题:(1)、如图所示的甲、乙两个平面图形能折什么几何体?
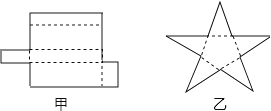 (2)、由多个平面围成的几何体叫做多面体.若一个多面体的面数为f , 顶点个数为v , 棱数为e , 分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?(3)、应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
(2)、由多个平面围成的几何体叫做多面体.若一个多面体的面数为f , 顶点个数为v , 棱数为e , 分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?(3)、应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.