(北师大版)2023-2024学年八年级数学上册4.3 一次函数的图像 同步测试
试卷更新日期:2023-09-12 类型:同步测试
一、选择题
-
1. 已知一次函数 , 若随的增大而减小,则它的图象经过( )A、第一、二、三象限 B、第一、二、四象限 C、第二、三、四象限 D、第一、三、四象限2. 直线与在同一平面直角坐标系内,其位置可能是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知正比例函数y=kx的图象经过点(-2,1),则k的值( )A、-2 B、- C、2 D、4. 在一次函数中,随的增大而增大,且 , 则在坐标系中它的大致图象是( )A、
3. 已知正比例函数y=kx的图象经过点(-2,1),则k的值( )A、-2 B、- C、2 D、4. 在一次函数中,随的增大而增大,且 , 则在坐标系中它的大致图象是( )A、 B、
B、 C、
C、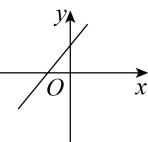 D、
D、 5. 如图,长方形的边在轴上,与原点重合, , , 点的坐标为.则直线的函数表达式为( )
5. 如图,长方形的边在轴上,与原点重合, , , 点的坐标为.则直线的函数表达式为( ) A、 B、 C、 D、6. 已知(m,n是不为0的常数),则下列描述正确的是( )A、若 , 则当x的值增大时,y的值也随之增大 B、若 , 则当x的值增大时,y的值也随之增头 C、若m,n同号,则当x的值增大时,y的值也随之增大 D、若m,n异号,则当x的值增大时,y的值也随之增大7. 下列各点一定在函数的图象上的是( )A、 B、 C、 D、8. 已知点和点在直线上,且 , 则a的值可能是( )A、-3 B、-2 C、1 D、39. 在平面直角坐标系中,将直线l1:平移后得到直线l2: , 则下列平移作法中,正确的是( )A、将直线l1向上平移6个单位 B、将直线l1向上平移3个单位 C、将直线l1向上平移2个单位 D、将直线l1向上平移4个单位10. 若一次函数y=(m-3)x-4的图象经过点A(x1 , y1)和点B(x2 , y2),当x1 > x2时,y1>y2 , 则m的取值范围是( )A、m<3 B、m>3 C、m≤3 D、m≥3
A、 B、 C、 D、6. 已知(m,n是不为0的常数),则下列描述正确的是( )A、若 , 则当x的值增大时,y的值也随之增大 B、若 , 则当x的值增大时,y的值也随之增头 C、若m,n同号,则当x的值增大时,y的值也随之增大 D、若m,n异号,则当x的值增大时,y的值也随之增大7. 下列各点一定在函数的图象上的是( )A、 B、 C、 D、8. 已知点和点在直线上,且 , 则a的值可能是( )A、-3 B、-2 C、1 D、39. 在平面直角坐标系中,将直线l1:平移后得到直线l2: , 则下列平移作法中,正确的是( )A、将直线l1向上平移6个单位 B、将直线l1向上平移3个单位 C、将直线l1向上平移2个单位 D、将直线l1向上平移4个单位10. 若一次函数y=(m-3)x-4的图象经过点A(x1 , y1)和点B(x2 , y2),当x1 > x2时,y1>y2 , 则m的取值范围是( )A、m<3 B、m>3 C、m≤3 D、m≥3二、填空题
-
11. 已知(-3,)(-1,)( , )是直线上的三个点,则y1、y2、y3的大小关系是 . (用“<”连接)12. 已知正比例函数经过点 , 则k的值是.13. 若关于x的方程有且只有一个解,则a的取值范围为.14. 已知正比例函数的图象经过第二、四象限,若点在该函数的图象上,则ab.(填“>”“<”或“=”)15. 在一次函数y=(k-2)x+1的图象经过第一、二、四象限,则k的取值范围为 .
三、解答题
-
16. 如图,将直线向上平移2个单位,得到一个一次函数的图象,求这个一次函数的表达式.
 17. 已知一次函数y=ax-3,当x=1时,y=7,当x=-2时,求y的值.18. 已知关于的一次函数 , 其图象经过第一、三、四象限,求的取值范围.19. 已知 , 与x成正比例,与成正比例,当时,;当时, , 求y与x之间的函数关系式.
17. 已知一次函数y=ax-3,当x=1时,y=7,当x=-2时,求y的值.18. 已知关于的一次函数 , 其图象经过第一、三、四象限,求的取值范围.19. 已知 , 与x成正比例,与成正比例,当时,;当时, , 求y与x之间的函数关系式.四、综合题
-
20. 已知y关于x的一次函数 , 当时,;当时,.(1)、求k、b的值;(2)、若 , 是该一次函数图象上的两点,求证:.21. 已知y与x之间成正比例关系,且当x=-1时,y=3.(1)、求y与x之间的函数关系式;(2)、当x=2时,求y的值.