安徽省安庆市桐城市2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-09-11 类型：期末考试

进入出卷网下载

一、单选题

1. 在 $- \sqrt{5}$ ， 0， $\frac{2}{3}$ ， $- 1$ 四个实数中，最小的是（　　）

A、 $\frac{2}{3}$ B、0 C、 $- 1$ D、 $- \sqrt{5}$

查看试题解析
2. 若 $a > b$ ，则下列不等式一定成立的是（　　）

A、 $a c > b c$ B、 $\frac{a}{3} < \frac{b}{3}$ C、 $a - 3 > b - 3$ D、 $- a > - b$

查看试题解析
3. 下列计算正确的是（　　）

A、 $3 m \cdot (2 m - 1) = 6 m^{2} + 3 m$ B、 $2 m^{2} n \div m^{2} = 2 m$ C、 ${(2 m)}^{3} = 8 m^{3}$ D、 ${(m + n)}^{2} = m^{2} + n^{2}$

查看试题解析
4. 当我们受到病毒感染时，我们的免疫系统很快就会作出反应，并派出免疫细胞将对方收拾掉，在我们体内的某种免疫细胞的直径约为 $0.000012$ 米，将数据 $0.000012$ 用科学记数法表示为（　　）

A、 $0.12 \times 1 0^{- 5}$ B、 $1.2 \times 1 0^{- 5}$ C、 $1.2 \times 1 0^{- 4}$ D、 $12 \times 1 0^{- 4}$

查看试题解析
5. 下列各数最接近 $\sqrt{5}$ 的是（　　）

A、1 B、2 C、3 D、4

查看试题解析
6. 若分式 $\frac{x^{2} - 9}{x^{2} - 3 x}$ 的值为 $0$ ，则 $x$ 的值为（　　）

A、 $- 3$ B、 $3$ C、 $- 3$ 或 $3$ D、 $0$ 或 $3$

查看试题解析
7. 若不等式 $m x - n > 0$ 的解集为 $x < 1$ ，则不等式 $m x - 2 m - n > 0$ 的解集为（　　）

A、 $x < 1$ B、 $x > 1$ C、 $x < 3$ D、 $x > 3$

查看试题解析
8. 将一块等腰直角三角板 $A B C$ 按如图方式摆放（ $∠ A B C = 45 °$ ），其中直线 $l_{1} ∥ l_{2}$ ，点C落在直线 $l_{2}$ 上，若 $∠ 1 = 15 °$ ，则 $∠ 2$ 的度数是（　　）

A、 $30 °$ B、 $25 °$ C、 $20 °$ D、 $15 °$

查看试题解析
9. 若关于 $x$ 分式方程 $\frac{x - 2}{x - 4} = \frac{m}{4 - x}$ 有增根，则 $m$ 的值为（　　）

A、 $- 3$ B、 $- 2$ C、 $2$ D、 $4$

查看试题解析
10. 如图， $A D ∥ B C ， A B ∥ C D$ ，且 $C D$ 平分 $∠ A C F$ ， $C E$ 平分 $∠ A C B$ 交 $A B$ 于点M ，则下列结论不一定正确的是（　　）

A、 $∠ E C D = 90 °$ B、 $∠ A B C = ∠ B A C$ C、 $∠ A D C = ∠ B A C$ D、 $∠ B A C = 2 ∠ C E D$

查看试题解析

二、填空题

11. 16的算术平方根是

查看试题解析
12. 分解因式： $2 x^{3} - 8 x y^{2} =$ ．

查看试题解析
13. 要使 $(x + 3) (2 x^{2} + m x - 4)$ 的展开式中不含 $x^{2}$ 项，则m的值为．

查看试题解析
14. 如图，直线 $A B$ ， $C D$ 相交于点O ， $O E$ 平分 $∠ B O C$ ．

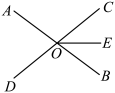(1)、若 $∠ A O D = α$ ，则 $∠ A O E =$ ．（用含α的式子表示）

(2)、若 $∠ A O D = 68 °$ ， $O F ⊥ C D$ ，则 $∠ E O F =$ ．

查看试题解析

三、解答题

15. 计算： ${(- 1)}^{2023} + \sqrt{9} - {(\sqrt{3} - 1)}^{0} + \sqrt[3]{- 8}$ ．

查看试题解析
16. 在如图所示的方格纸中，每个小正方形的边长为1，三角形 $A B C$ 的顶点均在格点（正方形网格线的交点）上．按下列要求画图：

(1)、过点C作 $C M ∥ A B$ ，使点M也在格点上，且 $C M = A B$ ．

(2)、在给定的方格纸中，平移三角形 $A B C$ ，使点A落在点D处，请画出平移后的三角形 $D E F$ ，使B ， C的对应点分别为E ， F ．

查看试题解析
17. 解分式方程： $\frac{2}{x - 2} = \frac{x}{3 x - 6} + 1$ ．

查看试题解析
18. 解不等式组 ${\begin{array}{l} 2 (x - 1) \leq 4 \\ \frac{x}{3} - 2 < x \end{array}$ ，并把解集在下列数轴上表示出来．

查看试题解析
19. 先化简，再求值： $\frac{x^{2} - 1}{x^{2} + 2 x + 1} \div \frac{x - 2}{x + 1} - \frac{x}{x - 2}$ ，其中 $x$ 是 $64$ 的立方根．

查看试题解析
20. 观察下列等式：
第1个等式： $\frac{1}{1 \times 2} - \frac{1}{2 \times 3} = \frac{2}{1 \times 2 \times 3}$ ．

第2个等式： $\frac{1}{2 \times 3} - \frac{1}{3 \times 4} = \frac{2}{2 \times 3 \times 4}$ ．

第3个等式： $\frac{1}{3 \times 4} - \frac{1}{4 \times 5} = \frac{2}{3 \times 4 \times 5}$ ．

……

按照以上规律，解决下列问题：

(1)、请直接写出第4个等式：．

(2)、写出你猜想的第n个等式（用含n的等式表示），并说明理由．

查看试题解析
21. 太和樱桃以成熟早、含糖量高、形美色艳而素负盛名，历史上曾被列为贡果．随着太和樱桃的上市，某果品店用 $2000$ 元购进了一批樱桃，过了一段时间又用 $5000$ 元购进了第二批樱桃，所购数量是第一批数量的2倍，但每千克樱桃的进价比第一批的进价贵了 $10$ 元．

(1)、该店第一批购进的樱桃有多少千克？

(2)、若该店两次购进的樱桃按相同的价格销售，全部售完后总利润不低于 $2000$ 元，则每千克樱桃的售价至少是多少元？

查看试题解析

22. 阅读与思考

整式乘法与因式分解是方向相反的变形．

$(x + p) (x + q) = x^{2} + (p + q) x + p q ，$ 得 $x^{2} + (p + q) x + p q = (x + p) (x + q)$ ．

利用这个式子可以将某些二次项系数是1的二次三项式进行因式分解，我们把这种方法称为“十字相乘法”．

例如：将式子 $x^{2} + 3 x + 2$ 分解因式．

解： $x^{2} + 3 x + 2 = x^{2} + (1 + 2) x + 1 \times 2 = (x + 1) (x + 2)$ .

请仿照上面的方法，解答下列问题：

(1)、分解因式：

x^{2} + 2 x - 8

．

(2)、分解因式：

x^{3} - 8 x^{2} + 12 x

．

(3)、若

x^{2} + p x - 6

可分解为两个一次因式的积，求整数p所有可能的值．

查看试题解析

23. 已知 $A B ∥ C D$ ， E是平面内一点，连接 $A E$ ， $C E$ ．

(1)、如图1，若 $∠ A = 160 °$ ， $∠ C = 135 °$ ，求 $∠ A E C$ 的度数．

(2)、如图2，当点E在 $C D$ 上方时，猜想 $∠ A$ ， $∠ C$ 与 $∠ A E C$ 之间的数量关系，并说明理由．

(3)、如图3， $A F$ 平分 $∠ B A E$ ，连接 $C F$ ， $∠ F C D = \frac{1}{6} ∠ E C D$ ，若 $∠ E = 30 °$ ， $∠ A F C = 40 °$ ， $∠ F C D$ 的度数．

查看试题解析