安徽省合肥市包河区2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-09-11 类型：期末考试

进入出卷网下载

一、单选题

1. 在下列给出的四个实数中，最小的实数是（）

A、0 B、 $- 1$ C、 $- \sqrt{2}$ D、2

查看试题解析
2. 下列各式中，计算结果为 $a^{6}$ 的是（）

A、 $a^{2} \cdot a^{3}$ B、 $a^{3} + a^{3}$ C、 $a^{12} \div a^{2}$ D、 ${(- a^{3})}^{2}$

查看试题解析
3. 如果 $a < b < 0$ ，下列不等式中错误的是（）

A、 $a b > 0$ B、 $\frac{a}{b} < 1$ C、 $a + b < 0$ D、 $a - b < 0$

查看试题解析
4. 下列式子从左到在变形正确的是（）

A、 $\frac{m^{2}}{n^{2}} = \frac{m}{n}$ B、 $\frac{m - 2}{n - 2} = \frac{m}{n}$ C、 $\frac{n + 5}{n + 1} = 5$ D、 $\frac{m}{- n} = \frac{- m}{n}$

查看试题解析
5. 如图， $∠ 1 = 68 °$ ，直线a平移后得到直线b ，则 $∠ 2 - ∠ 3$ 的度数为（）

A、 $132 °$ B、 $118 °$ C、 $112 °$ D、 $78 °$

查看试题解析
6. 如图，若x为正整数，则表示 $\frac{{(x + 2)}^{2}}{x^{2} + 4 x + 4} - \frac{1}{x + 1}$ 的值的点落在（　　）

A、段① B、段② C、段③ D、段④

查看试题解析
7. 某校购买了一批篮球和足球．已知购买足球的数量是篮球的2倍，购买足球用了5000元，购买篮球用了4000元，篮球单价比足球贵30元．根据题意可列方程 $\frac{5000}{2 x} = \frac{4000}{x} - 30$ ，则方程中x表示（）

A、足球的单价 B、篮球的单价 C、足球的数量 D、篮球的数量

查看试题解析
8. 将 ${(2 x)}^{n} - 81$ 因式分解后得 $(4 x^{2} + 9) (2 x + 3) (2 x - 3)$ ，那么n等于（）

A、2 B、4 C、6 D、8

查看试题解析
9. 若将一副三角板按如图所示的方式放置，其中 $∠ 2 = 30 °$ ，则下列结论不正确的是（）

A、 $∠ 1 = ∠ 3$ B、 $A C ∥ D E$ C、 $B C ∥ A D$ D、 $∠ 4 = ∠ C$

查看试题解析
10. 已知关于 $x$ 的方程 $\frac{x + m}{2} - \frac{x - m}{3} = 1$ 的解不大于1，且关于 $x$ 的不等式组 ${\begin{array}{l} 3 x - 6 \leq 0 \\ - m + 4 x > - 3 \end{array}$ 有且只有3个整数解，则符合条件的所有整数 $m$ 的和为（）.

A、2 B、3 C、5 D、6

查看试题解析

二、填空题

11. 若分式 $\frac{2}{x - 1}$ 有意义，则x的取值范围是．

查看试题解析
12. 有理数 $a$ ， $b$ 满足 $\sqrt{a + 4} + {(b - 2)}^{2} = 0$ ，则 $a - b =$ ．

查看试题解析
13. 如图所示，直线 $a$ 与直线 $b$ 交于点 $A$ ，与直线 $c$ 交于点 $B$ ， $∠ 1 = 12 0^{°}$ ， $∠ 2 = 4 5^{°}$ ．若使直线 $b$ 与直线 $c$ 平行，则可将直线 $b$ 绕点 $A$ 逆时针旋转．

查看试题解析
14. 定义一种新运算：对于任意的非零实数a，b，a $\otimes$ b= $\frac{1}{a} + \frac{1}{b}$ ．若(x+1) $\otimes$ x= $\frac{2 x + 1}{x}$ ，则x的值为

查看试题解析
15. 如图（1）所示为长方形纸带，将纸带沿EF折叠成图（2），再沿BF折叠成图（3），继续沿EF折叠成图（4），按此操作，最后一次折叠后恰好完全盖住∠EFG；整个过程共折叠了9次，问图（1）中∠DEF的度数是．

查看试题解析

三、解答题

16. 计算： $| - \sqrt{4} | + 2^{- 1} - (\sqrt{3} - 1)^{0}$ ．

查看试题解析
17. 解不等式组： ${\begin{matrix} x - 1 \leq 2 x ① \\ \frac{x + 1}{3} > \frac{x}{2} ② \end{matrix}$ ．

查看试题解析
18. 先化简， $(\frac{1}{x + 1} + \frac{1}{x^{2} - 1}) \div \frac{x}{x - 1}$ ，再从 $- 1$ ， $0$ ， $1$ ， $2$ 中选择一个合适的 $x$ 值代入求值．

查看试题解析
19. 如图，∠AFD＝∠1，AC∥DE．

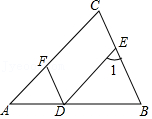(1)、试说明：DF∥BC；

(2)、若∠1＝68°，DF平分∠ADE，求∠B的度数．

查看试题解析
20. 已知AM∥CN ，点B为平面内一点，AB⊥BC于B ．

(1)、如图1，直接写出∠A和∠C之间的数量关系是；

(2)、如图2，过点B作BD⊥AM于点D ，求证：∠ABD=∠C ．

查看试题解析
21. 两个边长分别为 $a$ 和 $b$ 的正方形如图放置 $($ 图 $1)$ ，其未叠合部分 $($ 阴影 $)$ 面积为 $S_{1}$ ；若再在图 $1$ 中大正方形的右下角摆放一个边长为 $b$ 的小正方形 $($ 如图 $2)$ ，两个小正方形叠合部分 $($ 阴影 $)$ 面积为 $S_{2}$ ．

(1)、用含 $a$ ， $b$ 的代数式分别表示 $S_{1}$ 、 $S_{2}$ ；

(2)、若 $a + b = 8$ ， $a b = 13$ ，求 $S_{1} + S_{2}$ 的值．

查看试题解析
22. 某商场进货员预测一种应季T恤衫能畅销市场，就用4000元购进一批这种T恤衫，面市后果然供不应求.商场又用8800元购进了第二批这种T恤衫，所购数量是第一批购进量的2倍，但每件的进价贵了4元.

(1)、该商场购进第一批、第二批T恤衫每件的进价分别是多少元？

(2)、如果两批T恤衫按相同的标价销售，最后缺码的40件T恤衫按七折优惠售出，要使两批T恤衫全部售完后利润率不低于80%（不考虑其他因素），那么每件T恤衫的标价至少是多少元？

查看试题解析

四、填空题

23. 有正整数 $x < y < z$ ，且 $k$ 为整数， $\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = k$ ，则 $(y + z)^{x} =$ ．

查看试题解析