安徽省滁州市凤阳县2022-2023学年七年级下学期6月数学期末考试试卷

试卷更新日期：2023-09-11 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，国家节水标志由水滴，手掌和地球变形而成．以下可以通过平移节水标志得到的图形是（）

A、 B、 C、 D、

查看试题解析
2. 2的平方根是（　　　）

A、 $\sqrt{2}$ B、 $\pm \sqrt{2}$ C、±2 D、2

查看试题解析
3. 下列不等式的变形正确的是（　　）

A、由 $a < b$ ，得 $a c < b c$ B、由 $a c < b c$ ，得 $a < b$ C、由 $a < b$ ，得 $a + c < b + c$ D、由 $a - c > b - c$ ，得 $a < b$

查看试题解析
4. 已知若 $3 \cdot 3^{2 m} \cdot 3^{3 m} = 3^{26}$ ，则m等于（　　）

A、3 B、4 C、5 D、6

查看试题解析
5. 清代袁牧的一首诗《苔》中的诗句：“白日不到处，青春恰自来．苔花如米小，也学牡丹开．”若苔花的花粉直径约为0.0000084米，则数据0.0000084用科学记数法表示为（）

A、 $8.4 × 1 0^{- 5}$ B、 $8.4 \times 1 0^{- 6}$ C、 $8.4 × 1 0^{- 7}$ D、 $8.4 \times 1 0^{6}$

查看试题解析
6. 已知 $x^{2} - m x + 25$ 是完全平方式，则常数m的值为（）

A、10 B、 $\pm 10$ C、 $- 20$ D、 $\pm 20$

查看试题解析
7. 如果分式 $\frac{x^{2} - 4}{x - 2}$ 的值为0，那么x的值是（　　）

A、 $x = 2$ B、 $x = - 2$ C、 $x = 2$ 或 $- 2$ D、 $x = 0$

查看试题解析
8. 某特快列车在最近一次的铁路大提速后，时速提高了30千米/小时，则该列车行驶350千米所用的时间比原来少用1小时，若该列车提速前的速度是x千米/小时，下列所列方程正确的是（）

A、 $\frac{350}{x} - \frac{350}{x - 30} = 1$ B、 $\frac{350}{x} - \frac{350}{x + 30} = 1$ C、 $\frac{350}{x + 30} - \frac{350}{x} = 1$ D、 $\frac{350}{x - 30} - \frac{350}{x} = 1$

查看试题解析
9. 如图，直线 $A B$ 与直线 $C D$ 相交于点O ，若 $O E$ 平分 $∠ A O C$ ， $O F$ 平分 $∠ B O C$ ， $∠ B O F = 40 °$ ，则 $∠ C O E =$ （）

A、 $40 °$ B、 $50 °$ C、 $30 °$ D、 $60 °$

查看试题解析
10. 某市为了方便市民绿色出行，推出了共享单车服务，图①是某品牌共享单车放在水平地面的实物图，图②是其示意图，其中 $A B$ ， $C D$ 都与地面l平行， $∠ B C D = 62 °$ ， $∠ B A C = 54 °$ ，当 $∠ M A C$ 为（）度时， $A M$ 与 $C B$ 平行．

A、54 B、64 C、74 D、114

查看试题解析

二、填空题

11. 计算： ${(- 2)}^{2023} \times {(\frac{1}{2})}^{2023} =$ ．

查看试题解析
12. 若 $x + 2 y = 5$ ．则 $2 x^{2} + 8 x y + 8 y^{2} - 3 =$ ．

查看试题解析
13. 我们知道，同底数幂的乘法法则为： $a^{m} \cdot a^{n} = {a^{m}}^{+ n}$ （其中 $a \neq 0 ， m ， n$ 为正整数），类似地我们规定关于任意正整数 $m ， n$ 的一种新运算： $h (m + n) = h (m) \cdot h (n)$ ，若 $h (1) = k (k \neq 0)$ ，那么 $h (n) \cdot h (2023) =$ （用含 $n$ 和 $k$ 的代数式表示，其中 $n$ 为正整数）．

查看试题解析
14. 如图，将一张长方形纸片沿 $E F$ 折叠后，点 $D$ 、 $C$ 分别落在点 $D^{'}$ 、 $C^{'}$ 的位置， $E D^{'}$ 的延长线与 $B C$ 相交于点 $G$ ，若 $∠ E F G = 70 °$ ，则 $∠ 1 =$ ．

查看试题解析

三、解答题

15. 计算：

(1)、 $- 1^{2022} + {(- \frac{3}{2})}^{- 1} + \sqrt[3]{- 8} + {(3.14 - π)}^{0}$ ；

(2)、 $[x （ x^{2} y^{2} - x y ） - y （ x^{2} - x^{3} y ）] \div x^{2} y$ ．

查看试题解析
16. 已知不等式组： ${\begin{array}{l} 3 (2 x - 1) < 2 x + 8 \\ 2 + \frac{3 (x + 1)}{8} > 3 - \frac{x - 1}{4} \end{array}$ ，

(1)、求此不等式组的整数解；

(2)、若上述整数解满足不等式 $a x + 6 \leq x - 2 a$ ，化简 $| a + 1 | - | a - 1 |$ ．

查看试题解析
17. 先化简 $(\frac{a^{2} - 2 a + 1}{a^{2} - a} + \frac{a^{2} - 4}{a^{2} + 2 a}) \div \frac{2 a - 3}{a + 1}$ ；然后再从 $- 3$ ， $- 2$ ， $- 1$ ，0，1选择一个合适的数作为a的值，代入后再求值．

查看试题解析
18. 先观察下列等式，再回答问题：
① $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} = 1 + \frac{1}{1} - \frac{1}{2} = 1 \frac{1}{2}$ ；

② $\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} = 1 + \frac{1}{2} - \frac{1}{3} = 1 \frac{1}{6}$ ；

③ $\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} = 1 + \frac{1}{3} - \frac{1}{4} = 1 \frac{1}{12}$ ；

(1)、请根据上面三个等式提供的信息，猜想： $\sqrt{1 + \frac{1}{4^{2}} + \frac{1}{5^{2}}} =$ ＝；

(2)、请按照上面各等式的规律，计算 $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} + \sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} + \sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} + \dots + \sqrt{1 + \frac{1}{1 0^{2}} + \frac{1}{1 1^{2}}}$ 的值．

查看试题解析
19. 图1是一个长为 $4 b$ ，宽为 $a (a > b)$ 的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后按如图2所示的形状拼成一个大正方形．

(1)、图2中的阴影部分正方形的边长是（用含a，b的代数式表示）；

(2)、观察图1，图2，请写出 $(a + b)^{2} ， (a - b)^{2}$ ， $a b$ 之间的等量关系是：

(3)、已知 $(m + n)^{2} = 25 ， (m - n)^{2} = 16$ ，求 $m^{2} + n^{2}$ 的值．

(4)、如图3，C是线段 $A B$ 上的一点，以 $A C$ ， $B C$ 为边向上分别作正方形 $A C D E$ 和正方形 $B C F G$ ，连接 $A F$ ．若 $A B = 7 ， D F = 3$ ，求 $△ A F C$ 的面积．

查看试题解析
20.

(1)、将一个多项式分组后，可提公因式或运用公式继续分解的方法是分组分解法．例如： $a m + a n + b m + b n = (a m + a n) + (b m + b n) = a (m + n) + b (m + n) = (a + b) (m + n)$ ．
①分解因式： $a b - a - b + 1$ ；

②若 $a ， b$ $(a > b)$ 都是正整数且满足 $a b - a - b - 4 = 0$ ，求 $a + b$ 的值；

(2)、若 $a ， b$ 为实数且满足 $a b - a - b - 4 = 0$ ， $s = a^{2} + 3 a b + b^{2} + 3 a - \frac{5}{2} b$ ，求 $s$ 的最小值．

查看试题解析
21. 阅读材料：如果x是一个有理数，我们把不超过x的最大整数记作 $[x]$ ．
例如， $[3.2] = 3$ ， $[5] = 5$ ， $[- 2.1] = - 3$ ，那么， $x = [x] + a$ ，其中 $0 \leq a < 1$ ．

例如， $3.2 = [3.2] + 0.2$ ， $5 = [5] + 0$ ， $- 2.1 = [- 2.1] + 0.9$ ．

请你解决下列问题：

(1)、 $[4.8] =$ ， $[- 6.5] =$ ；

(2)、如果 $[x] = 5$ ，那么x的取值范围是；

(3)、如果 $[5 x - 2] = 3 x + 1$ ，那么x的值是；

(4)、如果 $x = [x] + a$ ，其中 $0 \leq a < 1$ ，且 $4 a = [x] + 1$ ，求x的值．

查看试题解析

22. 某汽车网站对两款价格相同，续航里程相同的汽车做了一次评测，一款为燃油车，另一款为纯电新能源车．得到相关数据如下：

燃油车	纯电新能源车
油箱容积：48升	电池容量：90千瓦时
油价：8元/升	电价： $0.6$ 元/千瓦时

(1)、设两款车的续航里程均为a千米，请用含a的代数式表示燃油车和纯电新能源车的每千米行驶费用；

(2)、若燃油车每千米行驶费用比纯电新能源车多

0.55

元．

①请分别求出这两款车的每千米行驶费用；

②若燃油车和纯电新能源车每年的其它费用分别为4800元和8100元．问：每年行驶里程超过多少千米时，新能源车的年费用更低？（年费用 $=$ 年行驶费用 $+$ 年其它费用）

查看试题解析

23. 如图1，E点在BC上，∠A＝∠D ， ∠ACB+∠BED＝180°．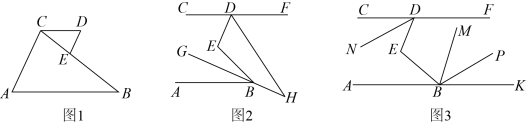

(1)、求证：AB∥CD；

(2)、如图2，AB∥CD ， BG平分∠ABE ，与∠EDF的平分线交于H点，若∠DEB比∠DHB大60°，求∠DEB的度数．

(3)、保持（2）中所求的∠DEB的度数不变，如图3，BM平分∠EBK ， DN平分∠CDE ，作BP∥DN ，则∠PBM的度数是否改变？若不变，请求值；若改变，请说明理由．

查看试题解析