安徽省六安市霍邱县2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-09-11 类型:期末考试
一、单选题
-
1. 的平方根为( )A、2 B、 C、4 D、2. 生物学家发现了一种病毒,其长度约为 , 它的用科学记数法表示正确的是( )A、 B、 C、 D、3. 下列计算中,正确的是( )A、 B、 C、 D、4. 满足的整数有几个?( )A、3 B、4 C、5 D、65. 如图,长方形的对角线 , , , 则图中五个小长方形的周长之和为( )
 A、7 B、9 C、14 D、186. 解不等式的过程如下:①去分母,得;②去括号,得;③移项,合并同类项,得;④系数化为1,得 . 其中错误的一步是( )A、① B、② C、③ D、④7. 如图所示,下列条件中能判定是( )
A、7 B、9 C、14 D、186. 解不等式的过程如下:①去分母,得;②去括号,得;③移项,合并同类项,得;④系数化为1,得 . 其中错误的一步是( )A、① B、② C、③ D、④7. 如图所示,下列条件中能判定是( )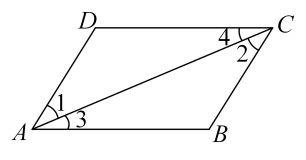 A、 B、 C、 D、8. 如图,直线 , 直线n上有一点A , 分别作射线 , 交直线m于点B , C , 且 , 已知 , 则的度数为( )
A、 B、 C、 D、8. 如图,直线 , 直线n上有一点A , 分别作射线 , 交直线m于点B , C , 且 , 已知 , 则的度数为( ) A、 B、 C、 D、9. 关于x的不等式组 的解集为x<2,那么a的取值范围为( )A、a=2 B、a>2 C、a<2 D、a≥210. 甲、乙两人分别从两地同时出发,若相向而行,则经过相遇;若同向而行,则经过甲追上乙.那么甲的速度是乙的( )A、倍 B、倍 C、倍 D、倍
A、 B、 C、 D、9. 关于x的不等式组 的解集为x<2,那么a的取值范围为( )A、a=2 B、a>2 C、a<2 D、a≥210. 甲、乙两人分别从两地同时出发,若相向而行,则经过相遇;若同向而行,则经过甲追上乙.那么甲的速度是乙的( )A、倍 B、倍 C、倍 D、倍二、填空题
-
11. 因式分解: =.12. 如果 , 则 .13. 已知 , 则 .14. 两块不同的三角板按如图1所示摆放,边与边重合, , 接着如图2保持三角板不动,将三角板绕着点(点不动)按顺时针(如图标示方向)旋转,在旋转的过程中,逐渐增大,当第一次等于时,停止旋转,在此旋转过程中,时,三角板有一条边与三角板的一条边恰好平行.
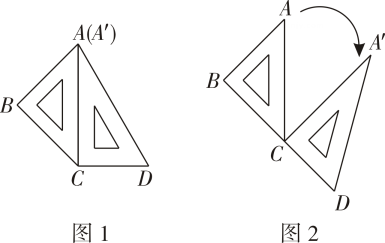
三、解答题
-
15. 计算:(1)、;(2)、 .16. 解不等式组 , 并把解集在数轴上表示出来.
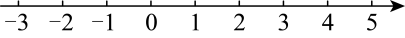 17. 解方程18. 先化简,再求值: , 请从中选择一个你认为可以代入的数值,将其代入化简后的式子,求值.19. 阅读材料并解答问题:我们已经知道,完全平方公式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,例如:就可以用图①的面积来表示.
17. 解方程18. 先化简,再求值: , 请从中选择一个你认为可以代入的数值,将其代入化简后的式子,求值.19. 阅读材料并解答问题:我们已经知道,完全平方公式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,例如:就可以用图①的面积来表示. (1)、请写出图②所表示的代数恒等式.(2)、请画图,用平面几何图形的面积来表示代数恒等式 .20. 观察下列各式:
(1)、请写出图②所表示的代数恒等式.(2)、请画图,用平面几何图形的面积来表示代数恒等式 .20. 观察下列各式:;
;
;
;
(1)、根据上面各式的规律可得: .(2)、根据上面各式的规律可得: .(3)、若 , 求的值.21. 我们知道完全平方公式是 , 由此公式我们可以得出以下结论:①;②;利用公式①和②解决下列问题:(1)、若 , 求的值.(2)、若满足 , 求的值.22. 某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.(1)、该商家购进的第一批衬衫是多少件?(2)、若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?23. 如图, , ),解答下列问题. (1)、如图①,当 , 时,过点B在的内部作则度;(2)、如图②,点G在上,过点G作 .
(1)、如图①,当 , 时,过点B在的内部作则度;(2)、如图②,点G在上,过点G作 .①当 , 时,求的度数;
②用含有和的式子表示;
③当 , 时,过点G作 , 直接写出的度数.