上海市长宁区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-09-11 类型:期末考试
一、单选题
-
1. 下列各数中,是无理数的是( )A、 B、 C、 D、2. 下列等式中,正确的是( )A、 B、 C、 D、3. 在直角坐标平面内,点P(﹣2,3)向下平移2个单位得到点Q,则点Q的坐标是( )A、(﹣2,1) B、(﹣2,5) C、(0,3) D、(﹣4,3)4. 下列图中 , 不是同位角的是( )A、
 B、
B、 C、
C、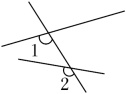 D、
D、 5. 已知三角形的两条边长分别为3和4,那么该三角形的第三条边长可能是( )A、1 B、3 C、7 D、96. 下面是“作的平分线”的尺规作图过程:
5. 已知三角形的两条边长分别为3和4,那么该三角形的第三条边长可能是( )A、1 B、3 C、7 D、96. 下面是“作的平分线”的尺规作图过程:①在、上分别截取、 , 使;②分别以点、为圆心,以大于的同一长度为半径作弧,两弧交于内的一点;
③作射线 .
就是所求作的角的平分线.

该尺规作图可直接利用三角形全等说明,其中三角形全等的依据是( )
A、三边对应相等的两个三角形全等 B、两边及它们的夹角对应相等的两个三角形全等 C、两角及它们的夹边对应相等的两个三角形全等 D、两角及其中一个角的对边对应相等的两个三角形全等二、填空题
-
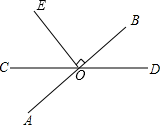
7. 16的四次方根是8. 把 表示成幂的形式是.9. 比较下列两实数的大小: .10. 用科学记数法表示,并保留三个有效数字: .11. 计算: .12. 在平面直角坐标系中,已知点在第二象限,且它到x轴、y轴的距离分别为2、3,那么点的坐标为 .13. 直角坐标平面内,经过点A(2,-3)并且垂直于y轴的直线可以表示为直线 .14. 如图,直线、相交于点 , 于点 , 且 , 则 .
 15. 如图, , 直线分别交、于点 , 平分交于点 . 如果 , , 即么的周长等于 .
15. 如图, , 直线分别交、于点 , 平分交于点 . 如果 , , 即么的周长等于 . 16. 如图,在△PAB中,PA=PB,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为
16. 如图,在△PAB中,PA=PB,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为 17. 如图,在中, , 点在边上,将沿着直线翻折,点B的对应点E恰好落在边上.如果 , 那么度.
17. 如图,在中, , 点在边上,将沿着直线翻折,点B的对应点E恰好落在边上.如果 , 那么度.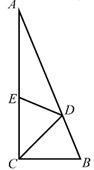 18. 在等腰△ABC中,如果过顶角顶点A的一条直线AD将△ABC分割成两个等腰三角形,那么∠BAC= .
18. 在等腰△ABC中,如果过顶角顶点A的一条直线AD将△ABC分割成两个等腰三角形,那么∠BAC= .三、解答题
-
19. 计算: .20. 利用幂的性质计算: .21. 如图,已知 , 请填写理由,说明 .
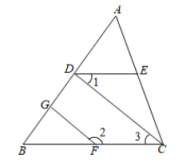
解:因为(已知),所以( )
得( )
又因为(已知),
所以( )
所以 ▲ ▲ ( )
所以( )
因为(已知),所以(垂直的意义)
得 ,
所以(垂直的意义)
22. 如图,已知 , 根据下列要求画图并回答问题: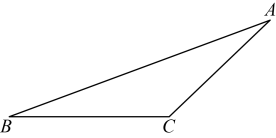 (1)、画边上的高 , 过点画直线 , 交于点;(不要求写画法和结论)(2)、在(1)的图形中,如果 , , , 求直线与间的距离.
(1)、画边上的高 , 过点画直线 , 交于点;(不要求写画法和结论)(2)、在(1)的图形中,如果 , , , 求直线与间的距离.

