四川省巴中市巴州区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-09-11 类型:期末考试
一、单选题
-
1. 下面图案中是轴对称图形的有( )
 A、1个 B、2个 C、3个 D、4个2. 下列运算正确的是( )A、 B、 C、 D、3. 下列等式成立的是( )A、 B、 C、 D、4. 下列事件中是必然事件的是( )A、小明的心率每分钟跳动次 B、三角形的一个外角大于它的一个内角 C、地球上,海洋面积大于陆地面积 D、手可摘星辰5. 如图, , 将含有的三角板如图放置,顶点D在直线之上,线段 , 分别与直线交于A , B两点, , 则的度数是( )
A、1个 B、2个 C、3个 D、4个2. 下列运算正确的是( )A、 B、 C、 D、3. 下列等式成立的是( )A、 B、 C、 D、4. 下列事件中是必然事件的是( )A、小明的心率每分钟跳动次 B、三角形的一个外角大于它的一个内角 C、地球上,海洋面积大于陆地面积 D、手可摘星辰5. 如图, , 将含有的三角板如图放置,顶点D在直线之上,线段 , 分别与直线交于A , B两点, , 则的度数是( ) A、 B、 C、 D、6. 如图, , , 添加一个条件,不能判断的是( )
A、 B、 C、 D、6. 如图, , , 添加一个条件,不能判断的是( )
 A、 B、 C、 D、7. 等腰三角形的周长为 , 一边长为 , 则其它两边长是( )A、 , B、 , C、 , 或 , D、 ,8. 用不同的方法计算几何图形的面积,可得数学等式.如图的数学等式是( )
A、 B、 C、 D、7. 等腰三角形的周长为 , 一边长为 , 则其它两边长是( )A、 , B、 , C、 , 或 , D、 ,8. 用不同的方法计算几何图形的面积,可得数学等式.如图的数学等式是( ) A、 B、 C、 D、9. 如图,强强想测量旗杆的高度,旗杆对面有一高为米的大楼 , 大楼与旗杆相距米(米),在大楼前米的点P处,测得 , 且 , , 则旗杆的高为( )
A、 B、 C、 D、9. 如图,强强想测量旗杆的高度,旗杆对面有一高为米的大楼 , 大楼与旗杆相距米(米),在大楼前米的点P处,测得 , 且 , , 则旗杆的高为( ) A、8米 B、米 C、米 D、米10. 以下四种情境分别描述了两个变量之间的关系:
A、8米 B、米 C、米 D、米10. 以下四种情境分别描述了两个变量之间的关系: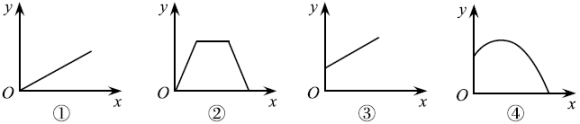
甲:运动员推铅球时,铅球的高度与水平距离的关系;
乙:食堂需购买一批餐具,支付费用与购餐具的数量的关系;
丙:一长方形水池里原有部分水,再匀速往里注水,水池中水面的高度与注水时间的关系;
丁:小明周末离家去看电影,结束后,原速度原路返回,小明离家的距离与时间的关系.
用下面的图象刻画上述情境,排序正确的是( )
A、③①④② B、④③①② C、④①③② D、③①②④11. 如图,在中, , , 点D是AC边上一动点,将沿直线翻折,使点A落在点F处,连接 , 交于点E , 当是直角三角形时,则的度数为( ) A、 B、 C、或 D、或12. 如图,在和中, , , , , 连接 , , 延长交于点F , 连接 . 下列结论:①;②;③;④平分 . 其中正确的结论个数有( )个.
A、 B、 C、或 D、或12. 如图,在和中, , , , , 连接 , , 延长交于点F , 连接 . 下列结论:①;②;③;④平分 . 其中正确的结论个数有( )个. A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
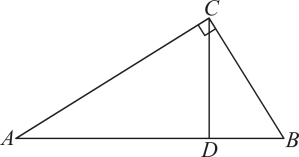
13. 如图,是的高, . 若 , 则的度数是 .
 14. 如图,在中,按以下步骤作图:①分别以点 , 为圆心,以大于的长为半径画弧,两弧相交于两点 , ;②作直线交于点 , 连接 . 若 , , , 则 .
14. 如图,在中,按以下步骤作图:①分别以点 , 为圆心,以大于的长为半径画弧,两弧相交于两点 , ;②作直线交于点 , 连接 . 若 , , , 则 . 15. 小东在生物书上看到这样一段话:“成熟的红细胞没有细胞核,平均直径为 , 正常成年男子每血液约含有红细胞个…”,他想算一算血液中红细胞排成一排大约有多长,通过计算发现大约有米.(用科学记数法表示.)16. 如图,在中, , 分别平分和 , 分别平分和 , 则 .
15. 小东在生物书上看到这样一段话:“成熟的红细胞没有细胞核,平均直径为 , 正常成年男子每血液约含有红细胞个…”,他想算一算血液中红细胞排成一排大约有多长,通过计算发现大约有米.(用科学记数法表示.)16. 如图,在中, , 分别平分和 , 分别平分和 , 则 . 17. 已知4组代数式 , , , , 从以上各代数式中任意抽取一个,能与构成完全平方式的概率为 .18. 阅读以下问题的解答过程:若多项式能被整除,求常数a的值.解法如下:
17. 已知4组代数式 , , , , 从以上各代数式中任意抽取一个,能与构成完全平方式的概率为 .18. 阅读以下问题的解答过程:若多项式能被整除,求常数a的值.解法如下:∵二次三项式中最高次项是 , 已知因式中最高次项是x ,
又∵ ,
∴另一因式的最高次项应为 . 因此,可设另一因式为(其中m是常数项).
即得, . ∴ .
可得 , . ∴ , .
仿照以上解题方法,解答以下问题:已知被整除,则k的值为 .
三、解答题
-
19.(1)、计算: .(2)、若规定 , 已知 , , 求的值.(3)、先化简,再求值: , 其中 .20. 三阶幻方是指将9个数填入九宫格中,要求每一横行,每一竖列以及对角线上的3个数之和相等.如图1就是一个幻方,图2是一个未完成的幻方,根据图2求的值.
 21. 如图,在正方形网格中有一个 .
21. 如图,在正方形网格中有一个 . (1)、画出关于直线的对称图形;(2)、若网格上的每个小正方形边长均为1,求的面积;22. 为了促进学生的全面发展,丰富学生的课余生活,学校五一假期组织学生参加公益活动.活动有义务植树、敬老院慰问、维护道路交通和社区服务.七年级5班共有50名同学,随机分配15名同学去义务植树,20名同学去敬老院慰问,5名同学去维护道路交通,剩下10名同学社区服务.(1)、该班小明同学被分配去敬老院慰问的概率是多少?(2)、由于放假前夕刚刚下雨,考虑到山坡地区不安全,学校取消了义务植树活动,现将这15名同学分配到其它活动中,若最终维护道路交通的同学占全班人数的 , 且分去敬老院和社区服务的学生人数相等,求社区服务的学生占全班的百分比.23. 如图,已知为的外角,平分 , 且 , 过点作于点 , 交于点 , 为边上一点,平分 .
(1)、画出关于直线的对称图形;(2)、若网格上的每个小正方形边长均为1,求的面积;22. 为了促进学生的全面发展,丰富学生的课余生活,学校五一假期组织学生参加公益活动.活动有义务植树、敬老院慰问、维护道路交通和社区服务.七年级5班共有50名同学,随机分配15名同学去义务植树,20名同学去敬老院慰问,5名同学去维护道路交通,剩下10名同学社区服务.(1)、该班小明同学被分配去敬老院慰问的概率是多少?(2)、由于放假前夕刚刚下雨,考虑到山坡地区不安全,学校取消了义务植树活动,现将这15名同学分配到其它活动中,若最终维护道路交通的同学占全班人数的 , 且分去敬老院和社区服务的学生人数相等,求社区服务的学生占全班的百分比.23. 如图,已知为的外角,平分 , 且 , 过点作于点 , 交于点 , 为边上一点,平分 . (1)、求证:;(2)、若 , , 求的度数.24. 小明星期天从家出发去小强家给小强过生日,他骑了一段时间后自行车发生故障,只能原地等待,同时电话联系小强,小强立刻骑自行车来接他,与小强相遇后,他搭乘小强的自行车一同去往小强家(两人接打电话和碰头,重新上车的时间均忽略不计),骑行速度变为之前小强骑行速度的一半.在这过程中,两人离小明家的距离s(千米)与小明所用时间t(小时)之间的关系如图所示,请根据图中信息,回答下列问题.
(1)、求证:;(2)、若 , , 求的度数.24. 小明星期天从家出发去小强家给小强过生日,他骑了一段时间后自行车发生故障,只能原地等待,同时电话联系小强,小强立刻骑自行车来接他,与小强相遇后,他搭乘小强的自行车一同去往小强家(两人接打电话和碰头,重新上车的时间均忽略不计),骑行速度变为之前小强骑行速度的一半.在这过程中,两人离小明家的距离s(千米)与小明所用时间t(小时)之间的关系如图所示,请根据图中信息,回答下列问题. (1)、两家相距千米;发生故障后,小明原地休息了小时与小强相遇;相遇前,小强骑行速度是千米/小时;(2)、求a的值;(3)、小强在出发后多少小时与小明家相距10千米.25. 当已知三角形一边中点时,我们常通过“倍长中线”来构造全等的两个三角形,从而解决问题.
(1)、两家相距千米;发生故障后,小明原地休息了小时与小强相遇;相遇前,小强骑行速度是千米/小时;(2)、求a的值;(3)、小强在出发后多少小时与小明家相距10千米.25. 当已知三角形一边中点时,我们常通过“倍长中线”来构造全等的两个三角形,从而解决问题.如图,已知 , 点D是的中点,延长至点E , 使 , 连接 , 易得到 , 从而得到 , .

已知 , 点D是的中点.
 (1)、如图1,点E在上,延长交于点F , 且 , 求证:;小明同学应用倍长中线的方法,延长至点M , 使 , 连接 , 请你帮助他写出证明过程.(2)、如图2,点E , G在射线上,连接 , 延长交于点F , 若 , G为的中点,求证:;(3)、在(2)的条件下,若点M是线段的中点, , 垂直平分线段 , 在上有一动点P , 连接 , 当的周长最小时,求的度数.
(1)、如图1,点E在上,延长交于点F , 且 , 求证:;小明同学应用倍长中线的方法,延长至点M , 使 , 连接 , 请你帮助他写出证明过程.(2)、如图2,点E , G在射线上,连接 , 延长交于点F , 若 , G为的中点,求证:;(3)、在(2)的条件下,若点M是线段的中点, , 垂直平分线段 , 在上有一动点P , 连接 , 当的周长最小时,求的度数.