吉林省松原市乾安县2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-09-11 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中，无理数是（）

A、 $- \frac{1}{2}$ B、 $| - 2 |$ C、 $\sqrt{9}$ D、 $π$

查看试题解析
2. 在平面直角坐标系中，点 $P (\sqrt{3} ， - 3)$ 位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 空气是由多种气体混合而成的，为了简明扼要的介绍空气的组成情况，较好的描述数据，最适合使用的统计图是（）

A、扇形图 B、条形图 C、折线图 D、直方图

查看试题解析
4. 已知关于x的不等式组 ${\begin{array}{l} 3 x - m > 0 \\ x - 1 \leq 5 \end{array}$ 有四个整数解，则m的取值范围是（）

A、 $2 \leq m < 3$ B、 $6 \leq m < 9$ C、 $3 < m \leq 6$ D、 $5 < m ≤ 7$

查看试题解析
5. 在平面直角坐标系中，下列说法：①若点 $A (a ， b)$ 在坐标轴上，则 $a b = 0$ ；②若 $m$ 为任意实数，则点 $(2 ， m^{2})$ 一定在第一象限；③若点 $P$ 到 $x$ 轴的距离与到 $y$ 轴的距离均为2，则符合条件的点 $P$ 有2个；④已知点 $M (2 ， 3)$ ，点 $N (- 2 ， 3)$ ，则 $M N ∥ x$ 轴．其中正确的是（）

A、①④ B、②③ C、①③④ D、①②④

查看试题解析
6. 如图，已知DC‖EG，∠C=40°，∠A=70°，则∠AFE的度数为（）

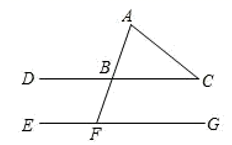A、140° B、110° C、90° D、30°

查看试题解析

二、填空题

7. 4的平方根是

查看试题解析
8. 已知点 $A (- 2 ， a + 3)$ 不在任何象限，则 $a =$ ．

查看试题解析
9. 规定用符合[x]表示一个实数的整数部分，例如[3.69]=3，[ $\sqrt{3}$ ]=1，按此规定[ $\sqrt{19}$ -1]=.

查看试题解析
10. 一组数据中的最小值是31，最大值是113，分析这组数据时，若取组距为10，则组数为．

查看试题解析
11. 若不等式 $(\sqrt{2} - a) x > \sqrt{2} - a$ 的解集是 $x < 1$ ，则a的取值范围是．

查看试题解析
12. “绿水青山就是金山银山”，某地准备购买一些松树和柏树绿化荒山，已知购买2棵松树和3棵柏树需要120元，购买2棵松树比1棵柏树多20元，设每棵松树 $x$ 元，每棵柏树 $y$ 元，则列出的方程组是．

查看试题解析
13. 如图，将一块三角尺的直角顶点放在直尺的一边上，当 $∠ 1 = 23 °$ 时， $∠ 2$ 的度数为．

查看试题解析
14. 如图，长方形 $A B C D$ 的长 $A B$ 为8，宽 $A D$ 为6，将这个长方形向上平移3个单位，再向左平移2个单位，得到长方形 $E F G H$ ，则阴影部分的面积为．

查看试题解析

三、解答题

15. 计算： $\sqrt{2^{2}} + \sqrt[3]{- 64} + | 1 - \sqrt{2} | - \sqrt{2} (\sqrt{2} - 3)$

查看试题解析
16. 解方程组： ${\begin{array}{l} 2 x + 3 y = 1 \\ 5 x - 6 y = 16 \end{array}$

查看试题解析
17. 解不等式组： ${\begin{array}{l} 3 x - 5 < x \\ \frac{x + 5}{3} - x \leq 1 \end{array}$ ，并写出它的所有整数解．

查看试题解析
18. 如图，已知 $∠ 1 + ∠ 2 = 180^{°}$ ， $∠ B = ∠ 3$ ，求证： $D E / / B C$ ．

查看试题解析
19. 如图，三角形 $A B C$ 中任意一点 $P (x_{0} ， y_{0})$ 经平移后对应点为 $P_{1} (x_{0} - 2 ， y_{0} - 3)$ ，将三角形 $A B C$ 作同样的平移得到三角形 $A_{1} B_{1} C_{1}$ ．

(1)、画出三角形 $A_{1} B_{1} C_{1}$ ；

(2)、请直接写出 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ 的坐标；

(3)、求三角形 $A_{1} B_{1} C_{1}$ 的面积．

查看试题解析
20. 如图，已知点 $A$ 、 $D$ 在直线 $E F$ 上， $∠ 1 + ∠ 2 = 180 °$ ， $D B$ 平分 $∠ A D C$ ， $A D ∥ B C$ ．

(1)、求证： $A B ∥ D C$ ；

(2)、若 $∠ D A B = 128 °$ ，求 $∠ D B C$ 的度数．

查看试题解析
21. 已知关于x、y的方程组 ${\begin{array}{l} 2 x + 3 y = 3 m + 7 \\ x - y = 4 m + 1 \end{array}$ 的解是一对正数；

(1)、试用m表示方程组的解；

(2)、求m的取值范围；

(3)、化简|m-1|+|m+ $\frac{2}{3}$ |．

查看试题解析
22. 《义务教育课程方案和课程标准2022年版》已经正式实施，新课程标准明确要求要设置劳动课程 $.$ 某学校七年级开始进行社会实践劳动，为了更好的设置学生喜欢的劳动课程，学校在七年级学生中对四项劳动内容A：校园种植花草；B：学校食堂帮厨；C：校园清洁；D：文明礼仪劝导 $)$ 开展了随机问卷调查，并对调查结果进行统计，结果如下：

请结合统计图回答下列问题：

(1)、该校抽样调查的学生人数为多少人？并补全条形统计图．

(2)、在扇形统计图中，请计算项目B所占扇形的圆心角是多少度？

(3)、若该校七年级共有学生600人，试估计该校七年级喜欢校园种植花草和学校食堂帮厨共有多少人．

查看试题解析
23. 已知方程组 ${\begin{array}{l} ax+by=15 ① \\ ax-by=- \frac{1}{2} ② \end{array}$ ，由于甲看错了方程①中的a，得到方程组的解为 ${\begin{array}{l} x=-3 \\ y=-1 \end{array}$ ；乙看错了②中的b，得到方程组的解为 ${\begin{array}{l} x=5 \\ y=4 \end{array}$ ．若按正确的a、b计算，求原方组的解．

查看试题解析
24. 探究：如图①， $E G ∥ F H$ ， OF平分 $∠ A F H$ ， OH平分 $∠ C H F$ ，且点O、E、G均在直线EG上，直线EG分别与AB、CD交于点E、G ．

(1)、若 $∠ A F H = 80 °$ ， $∠ C H F = 40 °$ ，则 $∠ F O H =$ ．

(2)、若 $∠ A F H + ∠ C H F = 110 °$ ，求 $∠ F O H$ 的度数．

(3)、如图②， $∠ A F H$ 和 $∠ C H I$ 的平分线FO、HO交于点O ， EG经过点O且平行于FH ，分别与AB、CD交于点E、G ．若 $∠ A F H + ∠ C H F = β$ ，直接写出 $∠ F O H$ 的度数．（用含 $β$ 的代数式表示）

查看试题解析
25. 某商店准备购进甲、乙两种品牌纪念品，若购进甲种纪念品 $40$ 个，乙种纪念品 $25$ 个，需要 $1350$ 元；若购进甲种纪念品 $20$ 个，乙种纪念品 $30$ 个，需要 $1200$ 元．

(1)、求购进甲、乙两种纪念品每个各需多少元？

(2)、若该商店刚好用了 $3000$ 元购进这两种纪念品，考虑顾客需求，要求购进甲种纪念品的数量不少于乙种纪念品数量的 $3$ 倍，且乙种纪念品数量大于 $38$ 个，那么该商店有几种进货方案？

(3)、若该商店销售每个甲种纪念品可获利润 $5$ 元，销售每个乙种纪念品可获利润 $6$ 元，在第（2）问的进货方案中，哪一种方案获利最大？最大利润是多少？

查看试题解析
26. 在平面直角坐标系中，点 $O$ 是坐标原点，点 $A$ 的坐标是 $(a ， - a)$ ，点 $B$ 的坐标是 $(b ， c)$ ，且 $a$ ， $b$ ， $c$ 满足 ${\begin{array}{l} 3 a - b + 2 c = 6 \\ a - 2 b - c = - 3 \end{array}$ ．

(1)、若 $a$ 为不等式 $2 x + 8 \leq 0$ 的最大整数解，判断点 $A$ 在第几象限，说明理由；

(2)、求点 $B$ 的坐标；

(3)、若有两个动点 $M (k - 1 ， k)$ 、 $N (- 3 h + 10 ， h)$ ，请探索是否存在以两个动点 $M$ 、 $N$ 为端点的线段 $M N ∥ A B$ ，且 $M N = A B$ ，若存在，求 $M$ 、 $N$ 两点的坐标；若不存在，请说明理由．

查看试题解析