北京市石景山区2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-09-11 类型:期末考试
一、单选题
-
1. 在平面直角坐标系xOy中,点关于原点对称的点的坐标是( )A、 B、 C、 D、2. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 解方程 , 下列用配方法进行变形正确的是( )A、 B、 C、 D、4. 一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定5. 下表是甲、乙两名同学八次射击测试成绩,设两组数据的平均数分别为 , , 方差分别为 , , 则下列说法正确的是( )
3. 解方程 , 下列用配方法进行变形正确的是( )A、 B、 C、 D、4. 一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定5. 下表是甲、乙两名同学八次射击测试成绩,设两组数据的平均数分别为 , , 方差分别为 , , 则下列说法正确的是( )
 A、 , B、 , C、 , D、 ,6. 某工厂由于采用新技术,生产量逐月增加,原来月产量为2000件,两个月后增至月产量为3000件. 若设月平均增长率为x , 则下列所列的方程正确的是( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,四边形是矩形,点 , , 将矩形绕点逆时针旋转 , 则旋转后点的对应点坐标为( )
A、 , B、 , C、 , D、 ,6. 某工厂由于采用新技术,生产量逐月增加,原来月产量为2000件,两个月后增至月产量为3000件. 若设月平均增长率为x , 则下列所列的方程正确的是( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,四边形是矩形,点 , , 将矩形绕点逆时针旋转 , 则旋转后点的对应点坐标为( ) A、 B、 C、 D、8. 小英以300米/分的速度匀速骑车8分钟到达某地,原地停留10分钟后以400米/分的速度匀速骑回出发地.小英距出发地的距离y(单位:千米)与时间x(单位:分)的函数图象可能是( )A、
A、 B、 C、 D、8. 小英以300米/分的速度匀速骑车8分钟到达某地,原地停留10分钟后以400米/分的速度匀速骑回出发地.小英距出发地的距离y(单位:千米)与时间x(单位:分)的函数图象可能是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 函数y= 的自变量x的取值范围是 .10. 已知是关于x的一元二次方程的一个根,则b的值是 .11. 根据某班40名学生身高的频数分布直方图(每组不含起点值,含终点值),回答下列问题:
 (1)、人数最多的身高范围是;(2)、身高大于175cm的学生占全班人数的百分比是 .12. 请写出一个图象平行于直线 , 且过第一、二、四象限的一次函数的表达式 .13. 已知点A(﹣2,y1),B(3,y2)在一次函数y=2x﹣3的图象上,则y1y2(填“>”,“<”或“=”).14. 如图,菱形的对角线 , 相交于点O , M , N分别是 , 边的中点,连接交于点P , 以下说法正确的是(填写序号即可).
(1)、人数最多的身高范围是;(2)、身高大于175cm的学生占全班人数的百分比是 .12. 请写出一个图象平行于直线 , 且过第一、二、四象限的一次函数的表达式 .13. 已知点A(﹣2,y1),B(3,y2)在一次函数y=2x﹣3的图象上,则y1y2(填“>”,“<”或“=”).14. 如图,菱形的对角线 , 相交于点O , M , N分别是 , 边的中点,连接交于点P , 以下说法正确的是(填写序号即可).① ② ③ ④
 15. 在平行四边形中, , , 过点D作于点H , 连接 . 若平分 , 则的长是 .
15. 在平行四边形中, , , 过点D作于点H , 连接 . 若平分 , 则的长是 . 16. 如图,在矩形中, , , 点P从点A出发,沿线段以每秒1个单位长度的速度向终点D运动;点Q从点B出发,沿线段以每秒2个单位长度的速度向终点A运动. P , Q两点同时出发,设点P运动的时间为(单位:秒),的面积为 . 则关于的函数表达式为 .
16. 如图,在矩形中, , , 点P从点A出发,沿线段以每秒1个单位长度的速度向终点D运动;点Q从点B出发,沿线段以每秒2个单位长度的速度向终点A运动. P , Q两点同时出发,设点P运动的时间为(单位:秒),的面积为 . 则关于的函数表达式为 .
三、解答题
-
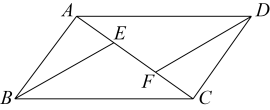
17. 解方程: .18. 一次函数()的图象经过点 , . 求一次函数的表达式.19. 已知:如图 E、F 是平行四边形 ABCD 的对角线 AC 上的两点,AF=CE. 求证:BE=DF.
 20. 在平面直角坐标系中,已知点 , , , 点A关于轴的对称点 .
20. 在平面直角坐标系中,已知点 , , , 点A关于轴的对称点 .
⑴在平面直角坐标系中作出点C , 点P;
⑵顺次连接 , 所得的四边形是(写出一种特殊四边形,不必证明).
21. 下面是证明三角形中位线定理的两种添加辅助线的方法,选择其中一种,完成证明.三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
已知:如图,在中,点D , E分别是 , 边的中点.求证: , 且 .
 (1)、方法一:证明:如图,延长到点 , 使 , 连接 , , .
(1)、方法一:证明:如图,延长到点 , 使 , 连接 , , .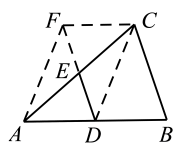 (2)、方法二:证明:如图,取中点 , 连接并延长到点 , 使 , 连接 .
(2)、方法二:证明:如图,取中点 , 连接并延长到点 , 使 , 连接 . 22. 甲、乙两人赛跑时,路程(单位:米)和时间(单位:秒)的关系如图所示,请你观察图象并回答:
22. 甲、乙两人赛跑时,路程(单位:米)和时间(单位:秒)的关系如图所示,请你观察图象并回答: (1)、这次赛跑的总路程有米.(2)、甲、乙两人中,的速度比较快.(3)、求出发2秒后,甲、乙两人的距离.23. 已知:在矩形中,是对角线.求作:菱形 , 使点分别在边上.
(1)、这次赛跑的总路程有米.(2)、甲、乙两人中,的速度比较快.(3)、求出发2秒后,甲、乙两人的距离.23. 已知:在矩形中,是对角线.求作:菱形 , 使点分别在边上.
作法:如图,①分别以点 , 为圆心,大于长为半径画弧,两弧在线段两侧分别交于点;
②作直线交于点 , 与分别交于点;
③连接 .
所以四边形就是所求的菱形.
根据上面设计的尺规作图过程,
(1)、使用直尺和圆规,补全图形(保留作图痕迹);(2)、完成下面的证明.证明:连接 .
∵ ,
∴是的垂直平分线( )(填推理根据).
∴ .
∴ .
∵四边形是矩形,
∴ ,
∴ .
∴ ▲ .
又 ,
∴ .
∴ .
∴ .
∴ .
又∵ ,
∴四边形是平行四边形( )(填推理根据).
又∵ ,
∴四边形是菱形( )(填推理根据).
24. 已知关于的一元二次方程 .(1)、请判断这个方程根的情况;(2)、若该方程有一个根小于1,求的取值范围.25. 如图,矩形草地中,m,m,点为边中点,草地内铺了一条长和宽分别相等直角折线甬路( , ),若草地总面积(两部分阴影之和)为 , 求甬路的宽. 26. 平面直角坐标系中,一次函数的图象与函数的图象交于点 .(1)、求的值;(2)、当时,对于的每一个值,函数的值大于函数的值,直接写出的取值范围.27. 如图,正方形中,点在上(与点不重合),连接 . 将线段绕点逆时针旋转 , 得到线段 , 过点作 , 交延长线于点 .
26. 平面直角坐标系中,一次函数的图象与函数的图象交于点 .(1)、求的值;(2)、当时,对于的每一个值,函数的值大于函数的值,直接写出的取值范围.27. 如图,正方形中,点在上(与点不重合),连接 . 将线段绕点逆时针旋转 , 得到线段 , 过点作 , 交延长线于点 . (1)、依题意补全图形;(2)、连接 , 试判断与的数量关系,并证明.28. 在平面直角坐标系中,如果点P到原点O的距离为a , 点M到点P的距离是a的k倍(k为正整数),那么称点M为点P的k倍关联点.
(1)、依题意补全图形;(2)、连接 , 试判断与的数量关系,并证明.28. 在平面直角坐标系中,如果点P到原点O的距离为a , 点M到点P的距离是a的k倍(k为正整数),那么称点M为点P的k倍关联点. (1)、当点的坐标为时,
(1)、当点的坐标为时,①如果点的2倍关联点M在y轴上,那么点M的坐标是;
如果点的2倍关联点M在x轴上,那么点M的坐标是;
②如果点是点的k倍关联点,且满足 , 那么k的最大值为;
(2)、如果点的坐标为 , 且在函数 的图象上存在的2倍关联点,直接写出b的取值范围.