吉林省延边州敦化市2022-2023学年七年级下学期期末数学试卷

试卷更新日期：2023-09-11 类型：期末考试

进入出卷网下载

一、选择题（本大题共6小题，共12.0分。在每小题列出的选项中，选出符合题目的一项）

1. $\frac{1}{4}$ 的平方根是（）

A、 $\frac{1}{2}$ B、 $\pm \frac{1}{2}$ C、2 D、士 $2$

查看试题解析
2. 在实数：3.14159， $\sqrt[3]{64}$ ， 1.010 010 001， $\sqrt{7}$ ， $π$ ， $\frac{2}{7}$ 中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 如果 $a > b$ ，下列各式中不正确的是（）

A、 $a - 3 > b - 3$ B、 $- \frac{a}{2} < - \frac{b}{2}$ C、 $- 2 a < - 2 b$ D、 $- 2 + a < - 2 + b$

查看试题解析
4. 下列 $4$ 个命题中，真命题的个数为（）（1）对顶角相等．（2）经过直线外一点，有且只有一条直线与这条直线平行．（3）在同一平面内，过一点有且只有一条直线与已知直线垂直．（4）两直线平行，同旁内角相等或互补．

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
5. 下列调查中，调查方式选择最合理的是（）

A、调查长江的水质情况，采用抽样调查 B、调查一批飞机零件的合格情况，采用抽样调查 C、检验一批进口罐装饮料的防腐剂含量，采用全面调查 D、企业招聘人员，对应聘人员进行面试，采用抽样调查

查看试题解析
6. 如图，将军要从村庄 $A$ 去村外的河边饮马，有三条路 $A B$ 、 $A C$ 、 $A D$ 可走，将军沿着 $A B$ 路线到的河边，他这样做的道理是（）

A、垂线段最短 B、点到直线的距离 C、两点确定一条直线 D、两点之间，线段最短

查看试题解析

二、填空题（本大题共8小题，共24.0分）

7. 在同一平面内，不重合的两条直线只有相交和两种位置关系．

查看试题解析
8. $\sqrt{(- 81)^{2}}$ 的平方根是， $\frac{1}{27}$ 的立方根是， $\sqrt{5} - 2$ 的绝对值是．

查看试题解析
9. 点 $A (4 ， 2)$ 先向右平移4个单位，再向下平移1个单位后的坐标为

查看试题解析
10. 命题“如果 $\frac{a}{c} = \frac{b}{c}$ ，那么 $a = b$ ”的题设是，这是一个命题 $($ 填“真”或“假” $)$ ．

查看试题解析
11. 若 $x$ ， $y$ 为实数，且 $| x + 2 | + \sqrt{y - 1} = 0$ ，则 $x y$ 的值为．

查看试题解析
12. 小明同学仿照我国古代经典的“鸡兔同笼”问题给小石同学出了一道题目：“今有鸡兔同笼，上有十二头，下有四十足，问鸡兔各几何？”．若小石同学设笼中有鸡x只，兔y只，则根据题意可列方程组为．

查看试题解析
13. 如图，将一块直角三角板与一张两边平行的纸条按照如图所示的方式放置，下列结论： $① ∠ 1 = ∠ 2$ ； $② ∠ 3 = ∠ 4$ ； $③ ∠ 2 = ∠ 3$ ； $④ ∠ 4 + ∠ 5 = 180 ° .$ 其中正确的是 $. ($ 填序号 $)$

查看试题解析
14. 如图，将 $△ A B C$ 沿 $B C$ 方向平移 $3 c m$ 得到 $△ D E F$ ，若 $△ A B C$ 的周长为 $18 c m$ ，则四边形 $A B F D$ 的周长为 $c m$ ．

查看试题解析

三、解答题（本大题共12小题，共84.0分。解答应写出文字说明，证明过程或演算步骤）

15. 计算： $3 \sqrt{2} + | 1 - \sqrt{2} | + \sqrt[3]{8} + \sqrt{36}$ ．

查看试题解析
16. 计算： ${\begin{array}{l} x - 2 y = 3 \\ 2 x + 8 y = 18 \end{array}$ ．

查看试题解析
17. 解不等式组 ${\begin{array}{l} 3 x + 7 \geq x + 1 \\ \frac{3 x + 4}{2} < x + 4 \end{array}$ 并将其解集表示在如图所示的数轴上．

查看试题解析
18. 表示实数 $a$ ， $b$ 的点在数轴上的位置如图所示，化简代数式 $\sqrt{(1 - a)^{2}} + | a - 2 | - | b + 1 | + \sqrt[3]{b^{3}}$ 的值．

查看试题解析
19. 如图， $E F ⊥ B C$ ， $∠ 1 = ∠ C$ ， $∠ 2 + ∠ 3 = 180 °$ ，试说明 $∠ A D C = 90 ° .$ 请完善解答过程，并在括号内填写相应的理论依据．
解： $∵ ∠ 1 = ∠ C$ ， $($ 已知 $)$
      $∴ G D / /$     ▲        （ $)$
      $∴ ∠ 2 = ∠ D A C .$ （ $)$
      $∵ ∠ 2 + ∠ 3 = 180 °$ ， $($ 已知 $)$
      $∴ ∠ D A C + ∠ 3 = 180 ° . ($ 等量代换 $)$
      $∴ A D / / E F .$ （ $)$
      $∴ ∠ A D C = ∠$     ▲        （ $)$
      $∵ E F ⊥ B C$ ， $($ 已知 $)$
      $∴ ∠ E F C = 90 ° .$ （ $)$
      $∴ ∠ A D C = 90 ° . ($ 等量代换 $)$

查看试题解析
20. 已知 $m + 3$ 的平方根是 $\pm 1$ ， $3 m + 2 n - 6$ 的立方根是4．

(1)、求 $m$ 、 $n$ 的值．

(2)、求 $m + n$ 的算术平方根．

查看试题解析
21. 如图，在平面直角坐标系中， $A$ 、 $B$ 、 $C$ 三点的坐标分别为 $(- 5 ， 4)$ 、 $(- 3 ， 0)$ 、 $(0 ， 2)$ ．

⑴画出三角形 $A B C$ ；

⑵三角形 $A' B' C'$ 是由三角形 $A B C$ 经过怎样的平移得到的；

⑶已知点 $P (a ， b)$ 为三角形 $A B C$ 内的一点，则点 $P$ 在三角形 $A' B' C'$ 内的对应点 $P'$ 的坐标是 ▲ ．

查看试题解析
22. 如图，已知∠A＝∠C，AD⊥BE，BC⊥BE，点E，D，C在同一条直线上.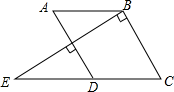

(1)、判断AB与CD的位置关系，并说明理由.

(2)、若∠ABC＝120°，求∠BEC的度数.

查看试题解析
23. 我市某中学开展课外体育活动，决定开设 $A$ ：篮球、 $B$ ：乒乓球、 $C$ ：踢毽子、 $D$ ：跑步四种体育活动项目 $.$ 为了解学生最喜欢哪一种活动项目 $($ 每人只选取一种 $)$ ，随机抽取了部分学生进行调查，并将调查结果绘成如图所示的统计图，请你结合图中信息解答下列问题．

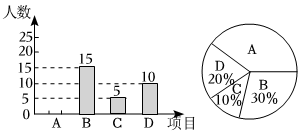(1)、样本中最喜欢 $A$ 项目的人数所占的百分比为多少？其在扇形统计图中对应的扇形的圆心角度数是多少度？

(2)、请把条形统计图补充完整；

(3)、若该校有学生 $2000$ 人，请根据样本估计全校最喜欢踢毽子的学生人数是多少？

查看试题解析
24. 为实现区域教育均衡发展，我市计划对某县 $A$ 、 $B$ 两类薄弱学校全部进行改造．根据预算，共需资金 $1575$ 万元改造一所 $A$ 类学校和两所 $B$ 类学校共需资金 $230$ 万元；改造两所 $A$ 类学校和一所 $B$ 类学校共需资金 $205$ 万元

(1)、改造一所 $A$ 类学校和一所 $B$ 类学校所需的资金分别是多少万元？

(2)、根据我市教育局规划计划今年对该县 $A$ 、 $B$ 两类学校进行改造，要求改造的 $A$ 类学校是 $B$ 类学校的 $2$ 倍多 $2$ 所，在计划投入资金不超过 $1555$ 万元的条件下，至多能改造多少所 $A$ 类学校？

查看试题解析
25. 已知一个角的两边与另一个角的两边分别平行，请结合图形回答下列问题：

(1)、如图 $①$ ， $A B / / C D$ ， $B E / / D F$ ，直接写出 $∠ 1$ 与 $∠ 2$ 的关系；

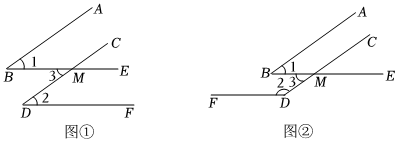(2)、如图 $②$ ， $A B / / C D$ ， $B E / / D F$ ，猜想 $∠ 1$ 与 $∠ 2$ 的关系，并说明理由；

(3)、由（1）（2），我们可以得出结论：一个角的两边与另一个角的分别平行，那么这两个角；

(4)、应用：两个角的两边分别平行，且一个角比另一个角的 $3$ 倍少 $60 °$ ，求出这两个角的度数分别是多少度？

查看试题解析
26. 如图，已知在平面直角坐标系中，OA＝OB＝4，BC＝12，点P的坐标是（a，6）．

(1)、直接写出 $△$ ABC顶点A，C的坐标；

(2)、若点P坐标为（1，6），连接PA，PB，求 $△$ PAB的面积；

(3)、是否存在点P，使 $△$ PAB的面积等于 $△$ ABC的面积？如果存在，请求出点P的坐标．

查看试题解析