吉林省白山市江源区2022-2023学年三校八年级下学期期末数学试卷
试卷更新日期:2023-09-11 类型:期末考试
一、选择题(本大题共6小题,共12.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 若等式成立,则内的运算符号是( )A、 B、 C、 D、2. 下列各组数中的三个数值分别为三角形的三边长,不能构成直角三角形的是( )A、3、4、5 B、5、12、13 C、 D、7、24、253. 计算的结果是( )A、 B、 C、 D、4. 一次函数中,随的增大而增大,且 , 则这个函数的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,菱形ABCD的边长为5cm,对角线BD与AC交于点O,若BD=6cm,则菱形ABCD的面积为( )
 A、48cm2 B、40cm2 C、30cm2 D、24 cm26. 如图,一次函数与一次函数的图象交于点 , 则关于的不等式的解集是( )
A、48cm2 B、40cm2 C、30cm2 D、24 cm26. 如图,一次函数与一次函数的图象交于点 , 则关于的不等式的解集是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共8小题,共24.0分)
-
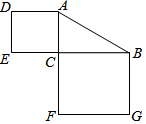
7. 在函数中,自变量的取值范围是 .8. 如图,在中, , 若 , 则正方形和的面积的和为 .
 9. 一直角三角形的两条直角边分别是和 , 则其斜边上中线的长度为 .10. 某中学规定学期总评成绩评定标准为:平时 , 期中 , 期末 , 小明平时成绩为分,期中成绩为分,期末成绩为分,则小明的学期总评成绩为分.11. 如图,在矩形中,对角线的垂直平分线分别交 , 于点 , , 连接 , , 如果 , 则
9. 一直角三角形的两条直角边分别是和 , 则其斜边上中线的长度为 .10. 某中学规定学期总评成绩评定标准为:平时 , 期中 , 期末 , 小明平时成绩为分,期中成绩为分,期末成绩为分,则小明的学期总评成绩为分.11. 如图,在矩形中,对角线的垂直平分线分别交 , 于点 , , 连接 , , 如果 , 则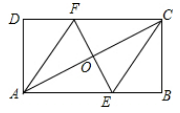 12. 如图,某中学开展了“书香校园”活动,班长小丽统计了本学期全班名同学课外图书的阅读量单位:本 , 绘制了统计图.如图所示,在这名学生的图书阅读量中,中位数是 .
12. 如图,某中学开展了“书香校园”活动,班长小丽统计了本学期全班名同学课外图书的阅读量单位:本 , 绘制了统计图.如图所示,在这名学生的图书阅读量中,中位数是 . 13. 如图,折叠矩形纸片的一边 , 使点落在边上的点处,BC=10cm,AB=8cm,则的长为 .
13. 如图,折叠矩形纸片的一边 , 使点落在边上的点处,BC=10cm,AB=8cm,则的长为 . 14. 如图,已知菱形ABCD的周长为16,面积为 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 .
14. 如图,已知菱形ABCD的周长为16,面积为 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 .
三、解答题(本大题共12小题,共84.0分。解答应写出文字说明,证明过程或演算步骤)
-
15. 计算: .16. 已知与成正比例,且当时, .(1)、写出与之间的函数关系式;(2)、当时,求的值.17. 如图,延长▱ABCD的边AD到F,使DF=DC,延长CB到点E,使BE=BA,分别连结点A、E和C、F.求证:AE=CF.
 18. 如图,四边形ABCD中,∠B=90°,AB=BC= ,CD=8,AD=10.
18. 如图,四边形ABCD中,∠B=90°,AB=BC= ,CD=8,AD=10. (1)、求∠BCD的度数;(2)、求四边形ABCD的面积.19. 图①,图②,图③都是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,在图③中已画出点A.按下列要求画图:
(1)、求∠BCD的度数;(2)、求四边形ABCD的面积.19. 图①,图②,图③都是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,在图③中已画出点A.按下列要求画图: (1)、在图①中,以格点为顶点,AB为一边画一个等腰三角形;(2)、在图②中,以格点为顶点,AB为一边画一个正方形;(3)、在图③中,以点A为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方形.20. 王大伯承包了一个鱼塘,投放了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.现将这20条鱼的质量作为样本,统计结果如图所示:
(1)、在图①中,以格点为顶点,AB为一边画一个等腰三角形;(2)、在图②中,以格点为顶点,AB为一边画一个正方形;(3)、在图③中,以点A为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方形.20. 王大伯承包了一个鱼塘,投放了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.现将这20条鱼的质量作为样本,统计结果如图所示: (1)、这20条鱼质量的中位数是 , 众数是.(2)、求这20条鱼质量的平均数;(3)、经了解,近期市场上这种鱼的售价为每千克18元,请利用这个样本的平均数.估计王大伯近期售完鱼塘里的这种鱼可收入多少元?21. 如图,在矩形中,是的中点,把矩形沿折叠,使点落在矩形外的一点上,连接并延长交的延长线于点 .
(1)、这20条鱼质量的中位数是 , 众数是.(2)、求这20条鱼质量的平均数;(3)、经了解,近期市场上这种鱼的售价为每千克18元,请利用这个样本的平均数.估计王大伯近期售完鱼塘里的这种鱼可收入多少元?21. 如图,在矩形中,是的中点,把矩形沿折叠,使点落在矩形外的一点上,连接并延长交的延长线于点 . (1)、求证:≌ .(2)、当 , 时,求的长.22. 如图 , 在中, , , 是的高,且 .
(1)、求证:≌ .(2)、当 , 时,求的长.22. 如图 , 在中, , , 是的高,且 . (1)、求的长;(2)、若是边上的一点,作射线 , 分别过点、作于点 , 于点如图 , 若 , 求与的和.23. 学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地两人之间的距离米与时间分钟之间的函数关系如图所示.
(1)、求的长;(2)、若是边上的一点,作射线 , 分别过点、作于点 , 于点如图 , 若 , 求与的和.23. 学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地两人之间的距离米与时间分钟之间的函数关系如图所示. (1)、根据图象信息,当 分钟时甲乙两人相遇,甲的速度为 米分钟;(2)、求出线段所表示的函数表达式.(3)、当为何值时,甲、乙两人相距米?24. 在正方形中,是边上一点点不与点、重合 , 连结 .
(1)、根据图象信息,当 分钟时甲乙两人相遇,甲的速度为 米分钟;(2)、求出线段所表示的函数表达式.(3)、当为何值时,甲、乙两人相距米?24. 在正方形中,是边上一点点不与点、重合 , 连结 . (1)、【感知】如图 , 过点作交于点易证≌不需要证明(2)、【探究】如图 , 取的中点 , 过点作交于点 , 交于点 .
(1)、【感知】如图 , 过点作交于点易证≌不需要证明(2)、【探究】如图 , 取的中点 , 过点作交于点 , 交于点 .①求证: .
②连结 , 若 , 则的长为 ▲ .
25. 在直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点分别作轴,轴的垂线,与坐标轴围成矩形的周长与面积相等,则点是和谐点.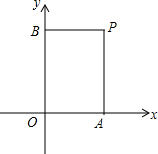 (1)、点 和谐点填“是”或“不是”;(2)、若点是和谐点,的值为 ;(3)、若(2)中和谐点在上,求的值.26. 如图,在矩形中,边上有一点 , 连结 , 若 , .
(1)、点 和谐点填“是”或“不是”;(2)、若点是和谐点,的值为 ;(3)、若(2)中和谐点在上,求的值.26. 如图,在矩形中,边上有一点 , 连结 , 若 , .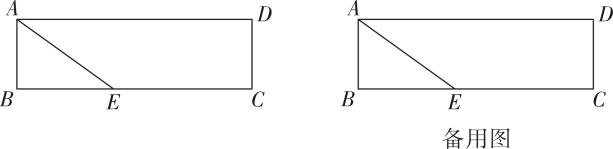 (1)、直接写出的长;(2)、有一点从点出发,以的速度沿向点运动,有一点从点出发,以的速度沿向点运动,当点到达点时,点、同时停止运动,设点的运动时间为秒.
(1)、直接写出的长;(2)、有一点从点出发,以的速度沿向点运动,有一点从点出发,以的速度沿向点运动,当点到达点时,点、同时停止运动,设点的运动时间为秒.秒时,四边形为平行四边形;
秒时,四边形为矩形;
(3)、有一点从点出发,以的速度沿向点运动,有一点从点出发,以的速度沿射线运动,当点到达点时,点、同时停止运动,设点的运动时间为秒,问取何值时,以、、、为顶点的四边形为平行四边形.