吉林省四平市铁东区2022-2023学年八年级下学期期末数学试卷
试卷更新日期:2023-09-11 类型:期末考试
一、选择题(本大题共6小题,共12.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 如图所示,▱ABCD的对角线AC,BD相交于点O,点E是CD的中点,若BC=6,则OE的长为( )
 A、2 B、2.5 C、3 D、43. 以下列长度的三条线段为边,能组成直角三角形的是( )A、2,3,4 B、3, , 5 C、5,12,13 D、4,4,84. 如图,正方形中,以对角线为一边作菱形 , 则等于( )
A、2 B、2.5 C、3 D、43. 以下列长度的三条线段为边,能组成直角三角形的是( )A、2,3,4 B、3, , 5 C、5,12,13 D、4,4,84. 如图,正方形中,以对角线为一边作菱形 , 则等于( )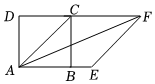 A、 B、 C、 D、5. 为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机抽取部分麦苗,获得苗高(单位:cm)的平均数与方差为: = =13, = =15:s甲2=s丁2=3.6,s乙2=s丙2=6.3.则麦苗又高又整齐的是( )
A、 B、 C、 D、5. 为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机抽取部分麦苗,获得苗高(单位:cm)的平均数与方差为: = =13, = =15:s甲2=s丁2=3.6,s乙2=s丙2=6.3.则麦苗又高又整齐的是( )
A、甲 B、乙 C、丙 D、丁6. 如图 , 动点从的顶点出发,沿匀速运动到点停止.在动点运动过程中,线段的长度与运动时间的函数关系如图所示,其中点为曲线部分的最低点,若的面积是 , 则图中的值为( )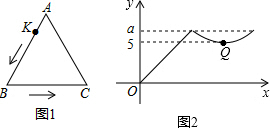 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共8小题,共24.0分)
-
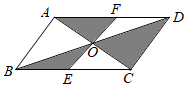
7. 化简: =.8. 小刚准备测量河水的深度,他把一根竹竿插到离岸边远的水底,竹竿高出水面 , 把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,河水的深度为9. 如图,平行四边形中,对角线、相交于点 , 过点的直线分别交、于点、 , 若 , , , 则图中阴影部分的面积是 .
 10. 如图,已知函数与函数的图象交于点 , 则方程组的解是 .
10. 如图,已知函数与函数的图象交于点 , 则方程组的解是 . 11. 如图,一次函数的图象与x轴交于点 , 则关于x的不等式的解集为 .
11. 如图,一次函数的图象与x轴交于点 , 则关于x的不等式的解集为 . 12. 若一次函数的图象经过第一、三、四象限,则的取值范围是 .13. 在中, , , 分别是 , , 所对的边.若 , , , 则最长边上的高是 .14. 如图,在菱形中,点是对角线上一点,连接 , 若 , 且 , , 则的长为 .
12. 若一次函数的图象经过第一、三、四象限,则的取值范围是 .13. 在中, , , 分别是 , , 所对的边.若 , , , 则最长边上的高是 .14. 如图,在菱形中,点是对角线上一点,连接 , 若 , 且 , , 则的长为 .
三、解答题(本大题共12小题,共84.0分。解答应写出文字说明,证明过程或演算步骤)
-
15. 计算: .16. 如图,在平行四边形中, , , 平分交于点 , 求的长.
 17. 如图
17. 如图 (1)、在直角坐标系中画出直线:;(2)、将直线向下平移个单位得到直线 , 请直接写出直线的函数解析式为: .18. 如图,已知四边形是平行四边形,、两点的坐标分别为 , .
(1)、在直角坐标系中画出直线:;(2)、将直线向下平移个单位得到直线 , 请直接写出直线的函数解析式为: .18. 如图,已知四边形是平行四边形,、两点的坐标分别为 , . (1)、点的坐标为: ;(2)、求直线的函数解析式.19. 如图,▱的对角线相交于点 , 是等边三角形, .
(1)、点的坐标为: ;(2)、求直线的函数解析式.19. 如图,▱的对角线相交于点 , 是等边三角形, . (1)、求证:▱是矩形;(2)、求四边形的面积.20. 如图,直线与轴交于点 , 与轴交于点 , 点是的中点.
(1)、求证:▱是矩形;(2)、求四边形的面积.20. 如图,直线与轴交于点 , 与轴交于点 , 点是的中点. (1)、在轴上存在点 , 使得 , 求点的坐标;(2)、在轴上是否存在一点 , 使得是直角三角形?若存在,请直接写出点的坐标;若不存在,请说明理由.21. 如图,四边形的对角线、相交于点 , , , 且 , , .
(1)、在轴上存在点 , 使得 , 求点的坐标;(2)、在轴上是否存在一点 , 使得是直角三角形?若存在,请直接写出点的坐标;若不存在,请说明理由.21. 如图,四边形的对角线、相交于点 , , , 且 , , . (1)、试判定四边形的形状;(2)、若 , , 求四边形的面积.22. 为了全面了解学生的学习、生活及家庭的基本情况,加强学校、家庭的联系,梅灿中学积极组织全体教师开展“课外访万家活动”,王老师对所在班级的全体学生进行实地家访,了解到每名学生家庭的相关信息,先从中随机抽取15名学生家庭的年收入情况,数据如表:
(1)、试判定四边形的形状;(2)、若 , , 求四边形的面积.22. 为了全面了解学生的学习、生活及家庭的基本情况,加强学校、家庭的联系,梅灿中学积极组织全体教师开展“课外访万家活动”,王老师对所在班级的全体学生进行实地家访,了解到每名学生家庭的相关信息,先从中随机抽取15名学生家庭的年收入情况,数据如表:年收入(单位:万元) 2 2.5 3 4 5 9 13
家庭个数 1 3 5 2 2 1 1
(1)、求这15名学生家庭年收入的平均数、中位数、众数;
(2)、你认为用(1)中的哪个数据来代表这15名学生家庭年收入的一般水平较为合适?请简要说明理由.23. 如图,在中, , , 点从点出发沿方向以每秒个单位长的速度向点匀速运动,同时点从点出发沿方向以每秒个单位长的速度向点匀速运动,当其中一个点到达终点时,另一个点也随之停止运动设点、运动的时间是秒过点作于点 , 连接、 . (1)、四边形能够成为菱形吗?如果能,求出相应的值;(2)、当为何值时,为直角三角形?请直接写出相应的值为: .24. 甲、乙两家商场平时以同样价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中超过200元后的价格部分打7折.(1)、以x(单位:元)表示商品原价,y(单位:元)表示购物金额,分别就两家商场的让利方式写出y关于x的函数解析式;(2)、春节期间如何选择这两家商场去购物更省钱?25. 如图,在平面直角坐标系中,是坐标原点,正方形的顶点、分别在轴与轴上,已知正方形边长为 , 点为轴上一点,其坐标为 , 连接 , 点从点出发以每秒个单位的速度沿折线的方向向终点运动,当点与点重合时停止运动,运动时间为秒.
(1)、四边形能够成为菱形吗?如果能,求出相应的值;(2)、当为何值时,为直角三角形?请直接写出相应的值为: .24. 甲、乙两家商场平时以同样价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中超过200元后的价格部分打7折.(1)、以x(单位:元)表示商品原价,y(单位:元)表示购物金额,分别就两家商场的让利方式写出y关于x的函数解析式;(2)、春节期间如何选择这两家商场去购物更省钱?25. 如图,在平面直角坐标系中,是坐标原点,正方形的顶点、分别在轴与轴上,已知正方形边长为 , 点为轴上一点,其坐标为 , 连接 , 点从点出发以每秒个单位的速度沿折线的方向向终点运动,当点与点重合时停止运动,运动时间为秒.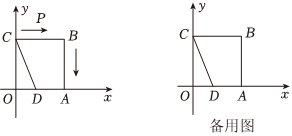 (1)、求线段的函数解析式;(2)、连接、 , 求的面积关于的函数解析式;(3)、点在运动过程中,是否存在某个位置使得为等腰三角形,若存在,直接写出点的坐标,若不存在,说明理由.26. 如图 , 四边形为菱形, . , , .
(1)、求线段的函数解析式;(2)、连接、 , 求的面积关于的函数解析式;(3)、点在运动过程中,是否存在某个位置使得为等腰三角形,若存在,直接写出点的坐标,若不存在,说明理由.26. 如图 , 四边形为菱形, . , , . (1)、点坐标为 ,四边形的面积为 ;(2)、如图 , 点在线段上运动,为等边三角形.
(1)、点坐标为 ,四边形的面积为 ;(2)、如图 , 点在线段上运动,为等边三角形.求证: , 并求的最小值;
点在线段上运动时,点的横坐标是否发生变化?若不变,请求出点的横坐标若变化,请说明理由.