广东省深圳市福田区八校2023-2024学年九年级上册数学开学联考试卷

试卷更新日期：2023-09-11 类型：开学考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. $\sqrt{2023}$ 的值介于（）

A、25与30之间 B、30与35之间 C、35与40之间 D、40与45之间

查看试题解析
2. 下列二次根式中，与 $\sqrt{2}$ 是同类二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{6}$ C、 $\sqrt{8}$ D、 $\sqrt{12}$

查看试题解析
3. 以下调查中，适宜全面调查的是（）

A、了解全班同学每周体育锻炼的时间 B、调查某批次汽车的抗撞击能力 C、调查春节联欢晚会的收视率 D、鞋厂检测生产的鞋底能承受的弯折次数

查看试题解析
4. 若代数式 $\frac{\sqrt{x}}{x - 2}$ 有意义，则实数 $x$ 的取值范围是（）

A、 $x \neq 2$ B、 $x \geq 0$ C、 $x \geq 2$ D、 $x \geq 0$ 且 $x \neq 2$

查看试题解析
5. 下列命题不正确的是（）

A、经过直线外一点，有且只有一条直线与这条直线平行 B、负数的立方根是负数 C、对角线互相垂直的四边形是菱形 D、五边形的外角和是360°

查看试题解析
6. 如图，工人师傅设计了一种测零件内径AB的卡钳，卡钳交叉点O为AA'、BB'的中点，只要量出A'B'的长度，就可以知道该零件内径AB的长度．依据的数学基本事实是（）

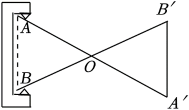A、两边及其夹角分别相等的两个三角形全等 B、两角及其夹边分别相等的两个三角形全等 C、两条直线被一组平行线所截，所得的对应线段成比例 D、两点之间线段最短

查看试题解析
7. 2020年-2022年无锡居民人均可支配收入由5.76万元增长至6.58万元，设人均可支配收入的平均增长率为x ，下列方程正确的是（）

A、5.76（1+x）²＝6.58 B、5.76（1+x²）＝6.58 C、5.76（1+2x）＝6.58 D、5.76x²＝6.58

查看试题解析
8. 下列结论：
①若ab＞0，则a＞0，b＞0，

②数0.00314用科学记数法表示为3.14×10^-⁴ ，

③若关于x的方程 $\frac{m}{x - 2} = \frac{1 - x}{x - 2}$ 有增根，则m＝1，

④ $\frac{π}{2}$ 不是分数，

⑤若关于x的不等式x+5＜2a恰有2个正整数解，则a的最大值是4．

以上结论正确的个（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
9. 小王同学从家出发，步行到离家a米的公园晨练，4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练，爸爸到达公园后立即以原速折返回到家中，两人离家的距离y（单位：米）与出发时间x（单位：分钟）的函数关系如图所示，则两人先后两次相遇的时间间隔为（）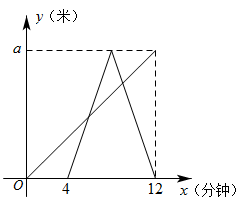

A、2.7分钟 B、2.8分钟 C、3分钟 D、3.2分钟

查看试题解析
10. 如图，平行四边形ABCD中，AB＝16，AD＝12，∠A＝60°，E是边AD上一点，且AE＝8，F是边AB上的一个动点，将线段EF绕点E逆时针旋转60°，得到EG ，连接BG、CG ，则BG+CG的最小值是（）

A、4 B、4 $\sqrt{15}$ C、4 $\sqrt{21}$ D、4 $\sqrt{37}$

查看试题解析

二、填空题（每题3分，共15分）

11. 计算：a⁴·(-a)³＝．

查看试题解析
12. 如图，已知直线AB∥CD ， EG平分∠BEF ， ∠1＝40°，则∠2的度数是．

查看试题解析
13. 若实数m满足（m-2023）²+（2024-m）²＝2025，则（m-2023）（2024-m）＝．

查看试题解析
14. 数学家高斯推动了数学科学的发展，被数学界誉为“数学王子”，据传，他在计算1+2+3+4+⋯+100时，用到了一种方法，将首尾两个数相加，进而得到1+2+3+4+⋯+100＝ $\frac{100 \times (1 + 100)}{2}$ ．人们借助于这样的方法，得到1+2+3+4+⋯+n＝ $\frac{n (1 + n)}{2}$ （n是正整数）．有下列问题，如图，在平面直角坐标系中的一系列格点A_i（x_i ， y_i），其中i＝1，2，3，⋯，n ， ⋯，且x_i ， y_i是整数．记a_n＝x_n+y_n ，如A₁（0，0），即a₁＝0，A₂（1，0），即a₂＝1，A₃（1，-1），即a₃＝0，⋯，以此类推．则a₂₀₂₃＝．

查看试题解析
15. 如图，在△ABC中，AB＝AC ， ∠BAC＝90°，D为AC边上一动点，且不与点A、点C重合，连接BD并延长，在BD延长线上取一点E ，使AE＝AB＝AC ，连接CE ．过点A作AF⊥BE于点F ， AF的延长线与EC的延长线交于点H ，已知AB＝6，CH＝3，则EH＝．

查看试题解析

三、解答题（共55分）

16. 计算：

(1)、 $| - 2023 | + π^{0} - {(\frac{1}{6})}^{- 1} + \sqrt{16}$ ；

(2)、 $(1 + \frac{1}{m}) \div \frac{m^{2} - 1}{m}$ ．

查看试题解析
17. 习近平总书记说：“读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然正气．”某校为提高学生的阅读品味，现决定购买获得茅盾文学奖的甲，乙两种书共100本，已知购买2本甲种书和1本乙种书共需100元；购买3本甲种书和2本乙种书共需165元．

(1)、求甲，乙两种书的单价分别为多少元；

(2)、若学校决定购买以上两种书的总费用不超过3200元，那么该校最多可以购买甲种书多少本？

查看试题解析
18. 如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点，△ABC的顶点均在格点上，O、M也在格点上．

⑴画出△ABC关于直线OM对称的△A₁B₁C₁；

⑵画出△ABC绕点O按顺时针方向旋转90°后所得的△A₂B₂C₂；

⑶△A₁B₁C₁与△A₂B₂C₂组成的图形是轴对称图形吗？如果是轴对称图形，请画出对称轴．

查看试题解析
19. 2023年3月27日是第28个全国中小学生安全教育日，为提高学生安全防范意识和自我防护能力，某学校举行了校园安全知识竞赛活动．现从八、九年级中各随机抽取15名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分用x表示，80分及以上为优秀，共分成四组，A： $60 \leq x < 70$ ；B： $70 \leq x < 80$ ；C： $80 \leq x < 90$ ；D： $90 \leq x \leq 100$ ），并给出下面部分信息：
八年级抽取的学生竞赛成绩在C组中的数据为：84，84，88．
九年级抽取的学生竞赛成绩为：68，77，75，100，80，100，82，86，95，91，100，86，84，94，87．

八、九年级抽取的学生竞赛成绩统计表
年级
平均数
中位数
众数
优秀率
八
87
a
98
$60 %$
九
87
86
b
c
根据以上信息，解答下列问题：

(1)、填空： $a =$ ， $b =$ ， $c =$ ．

(2)、该校八、九年级共500人参加了此次竞赛活动，请你估计该校八、九年级参加此次竞赛活动成绩达到90分及以上的学生人数．

查看试题解析
20. 如图，BD是矩形ABCD的对角线．

(1)、作线段BD的垂直平分线（要求：尺规作图，保留作图痕迹，不必写作法和证明）；

(2)、设BD的垂直平分线交AD于点E ，交BC于点F ，连接BE ， DF ．
①判断四边形BEDF的形状，并说明理由；
②若AB＝5，BC＝10，求四边形BEDF的周长．

查看试题解析
21. 点P（x ， y）是第一象限内一个动点，过点P分别作两坐标轴的垂线，垂足分别为M ， N ，已知矩形PMON的周长为8．

(1)、求y关于x的函数关系式，直接写出自变量x的取值范围；

(2)、直线l与（1）中的函数图象交于A（1，a），与x轴交于点B（-1，0）．
①求直线l的解析式；

②已知点P不与点A重合，且△ABP的面积为 $\frac{5}{4}$ ，直接写出P点的坐标．

查看试题解析
22.

(1)、用数学的眼光观察
如图①，在四边形ABCD中，AD＝BC ， P是对角线BD的中点，M是AB的中点，N是DC的中点．求证：∠PMN＝∠PNM ．

(2)、用数学的思维思考
如图②，延长图①中的线段AD交MN的延长线于点E ，延长线段BC交MN的延长线于点F ．求证：∠AEM＝∠F ．

(3)、用数学的语言表达
如图③，在△ABC中，AC＜AB ，点D在AC上，AD＝BC ， M是AB的中点，N是DC的中点，连接MN并延长，与BC的延长线交于点G ，连接GD ．若∠ANM＝60°，试判断△CGD的形状，并进行证明．

查看试题解析

年级	平均数	中位数	众数	优秀率
八	87	a	98	$60 %$
九	87	86	b	c