吉林省白山市靖宇三中、七中2022-2023学年八年级下学期期末数学试卷

试卷更新日期：2023-09-11 类型：期末考试

进入出卷网下载

一、选择题（本大题共6小题，共12.0分。在每小题列出的选项中，选出符合题目的一项）

1. 下列二次根式是最简二次根式的是（）

A、 $\sqrt{\frac{1}{4}}$ B、 $\sqrt{5}$ C、 $\sqrt{24}$ D、 $\sqrt{32}$

查看试题解析
2. 一次函数 $y = 2 x - 3$ 的图象不经过的象限是（）

A、第一象限. B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 有一组数据： $4$ ， $6$ ， $6$ ， $6$ ， $8$ ， $9$ ， $12$ ， $13$ ，这组数据的中位数为（）

A、 $6$ B、 $7$ C、 $8$ D、 $9$

查看试题解析
4. 在四边形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 相交于点 $O$ ，下列条件不能判定这个四边形是平行四边形的是（）

A、 $A B / / D C$ ， $A D = B C$ B、 $A B = D C$ ， $A D = B C$ C、 $A O = C O$ ， $B O = D O$ D、 $A B / / D C$ ， $A D / / B C$

查看试题解析
5. 如图，A，B 两点被池塘隔开，在 AB 外选一点 C，连接 AC，BC，分别取 AC，BC 的中点D，E，连接 DE.若测得 DE=5，则 AB 的长为（）.

A、5 B、8 C、10 D、无法确定

查看试题解析
6. 如图所示的计算程序中，y与x之间的函数关系所对应的图象应为（）

A、 B、 C、 D、

查看试题解析

二、填空题（本大题共9小题，共29.0分）

7. 函数 $y = \sqrt{3} x + 6$ 中自变量 $x$ 的取值范围是．

查看试题解析
8. 在▱ $A B C D$ 中，如果 $∠ A + ∠ C = 200 °$ ，那么 $∠ B$ 的度数是度．

查看试题解析
9. 如图，在菱形 $A B C D$ 中， $E$ 为 $A B$ 上一点，沿 $C E$ 折叠 $△ B E C$ ，点 $B$ 恰好落在对角线 $A C$ 上的 $B'$ 处 $.$ 若 $∠ D A B = 56 °$ ，则 $∠ A E B'$ 的度数为 $° .$

查看试题解析
10. 已知一次函数 $y = (m - 3) x^{| m | - 2}$ ，则 $y$ 随 $x$ 的增大而．

查看试题解析
11. 直线 $l_{1}$ ： $y = k x$ 与直线 $l_{2}$ ： $y = a x + b$ 在同一平面直角坐标系中的图象如图，则关于 $x$ 的不等式 $a x + b > k x$ 的解集为．

查看试题解析
12. 已知一组数据 $- 1$ 、 $2$ 、 $x$ 、 $3$ 、 $1$ 的平均数等于 $1.4$ ，则这组数据的中位数等于．

查看试题解析
13. 如图，矩形 $A B C D$ 的对角线 $A C$ ， $B D$ 相交于点 $O$ ， $C E / / B D$ ， $D E / / A C .$ 若 $A C = 4$ ，则四边形 $C O D E$ 的周长是．

查看试题解析
14. 已知平面上点 $O (0 ， 0)$ ， $A (4 ， 2)$ ， $B (6 ， 0)$ ，直线 $y = m x - 4 m + 2$ 将 $△ O A B$ 分成面积相等的两部分，则 $m$ 的值为．

查看试题解析
15. 计算： $2 \sqrt{12} - 6 \sqrt{\frac{1}{3}} + 3 \sqrt{48}$ =.

查看试题解析

三、解答题（本大题共11小题，共79.0分。解答应写出文字说明，证明过程或演算步骤）

16. 如图所示，四边形 $A B C D$ 是矩形，把 $△ A C D$ 沿 $A C$ 折叠到 $△ A C D'$ ， $A D'$ 与 $B C$ 交于点 $E$ ，若 $A D = 4$ ， $D C = 3$ ，求 $B E$ 的长．

查看试题解析
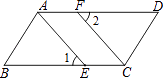
17. 已知：如图，点E，F分别为▱ABCD的边BC，AD上的点，且∠1=∠2．
求证：AE=CF．

查看试题解析
18. 一次函数图象经过 $(- 2 ， 1)$ 和 $(1 ， 7)$ 两点．

(1)、求这个一次函数的解析式；

(2)、当 $x = 3$ 时，求 $y$ 的值．

查看试题解析
19. 如图，在矩形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 相交于点 $O$ ，点 $E$ 、 $F$ 分别是 $A O$ 、 $A D$ 的中点，若 $A C = 10 c m$ ，求 $E F$ 的长度．

查看试题解析
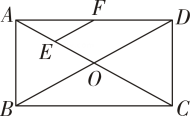20. 如图，在△ABC中，E点为AC的中点，其中BD=1，DC=3，BC= $\sqrt{10}$ ，AD= $\sqrt{7}$ ，求DE的长．

查看试题解析
21. 如图是由边长为 $1$ 的小正方形组成的网格，每个小正方形的顶点叫做格点 $.$ 点 $A$ ， $B$ 均在格点上 $.$ 仅用无刻度的直尺完成画图，画图过程用虚线，画图结果用实线表示，请按步骤完成下列问题．
⑴直接写出的 $A B$ 长为 ▲ ；
⑵在格点上找一点 $C$ ，连接 $B C$ ，使 $A B ⊥ B C$ ；
⑶画线段 $A B$ 的中点 $D$ ；
⑷在格点上找一点 $E$ ，连接 $D E$ ，使 $D E / / B C$ ．

查看试题解析
22.
在▱ABCD中，过点D作DE⊥AB于点E，点F 在边CD上，DF=BE，连接AF，BF．

(1)、求证：四边形BFDE是矩形；

(2)、若CF=3，BF=4，DF=5，求证：AF平分∠DAB

查看试题解析

23. 某校八年级两个班，各选派

10

名学生参加学校举行的“安全知识大赛”预赛，各参赛选手的成绩如下：

八（1）班： $93$ ， $98$ ， $89$ ， $93$ ， $95$ ， $96$ ， $93$ ， $96$ ， $98$ ， $99$ ；

八（2）班： $93$ ， $94$ ， $88$ ， $91$ ， $92$ ， $93$ ， $100$ ， $98$ ， $98$ ， $93$ ．

整理后得到数据分析表如下：

班级	最高分	平均分	中位数	众数	方差
八（1）班	$99$	$a$	$95.5$	$93$	$8.4$
八（2）班	$100$	$94$	$b$	$93$	$c$

(1)、填空：

a =

，

b =

；

(2)、求出表中

c

的值；

(3)、你认为哪个班级成绩好？请写出两条你认为该班成绩好的理由．

查看试题解析

24. 如图， $l_{A}$ 、 $l_{B}$ 分别表示 $A$ 步行与 $B$ 骑车在同一路上行驶的路程 $S$ 与时间 $t$ 的关系．

(1)、B出发时与 $A$ 相距千米．

(2)、B走了一段路后，自行车发生故障， $B$ 进行修理，所用的时间是小时．

(3)、B第二次出发后小时与 $A$ 相遇．

(4)、若 $B$ 的自行车不发生故障，保持出发时的速度前进，则出发多长时间与 $A$ 相遇？ $($ 写出过程 $)$

查看试题解析
25. 某校运动会需购买A，B两种奖品，若购买A种奖品3件和B种奖品2件，共需60元；若购买A种奖品5件和B种奖品3件，共需95元.

(1)、求A、B两种奖品的单价各是多少元？

(2)、学校计划购买A、B两种奖品共100件，购买费用不超过1150元，且A种奖品的数量不大于B种奖品数量的3倍，设购买A种奖品m件，购买费用为W元，写出W（元）与m（件）之间的函数关系式.求出自变量m的取值范围，并确定最少费用W的值.

查看试题解析
26. 已知，如图， $O$ 为坐标原点，四边形 $O A B C$ 为矩形， $A (10 ， 0)$ ， $C (0 ， 4)$ ，点 $D$ 是 $O A$ 的中点，动点 $P$ 在线段 $B C$ 上以每秒 $2$ 个单位长的速度由点 $C$ 向 $B$ 运动．设动点 $P$ 的运动时间为 $t$ 秒．

(1)、当 $t$ 为何值时，四边形 $P O D B$ 是平行四边形？

(2)、在直线 $C B$ 上是否存在一点 $Q$ ，使得 $O$ 、 $D$ 、 $Q$ 、 $P$ 四点为顶点的四边形是菱形？若存在，求 $t$ 的值，并求出 $Q$ 点的坐标；若不存在，请说明理由．

(3)、在线段 $P B$ 上有一点 $M$ ，且 $P M = 5$ ，当 $P$ 运动秒时，四边形 $O A M P$ 的周长最小，并写出点 $M$ 的坐标．

查看试题解析