辽宁省丹东市凤城市2023年中考数学毕业试卷
试卷更新日期:2023-09-11 类型:中考真卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 的相反数是( )A、 B、 C、 D、2. 下列计算正确的是( ).A、 B、 C、 D、3. 一个几何体的三视图如图所示,则这个几何体是( )
 A、球体 B、圆柱 C、圆锥 D、棱柱4. 下列说法正确的个数是( )
A、球体 B、圆柱 C、圆锥 D、棱柱4. 下列说法正确的个数是( )①0.01的立方根是0.000001;②如果一个角的两边分别平行于另一个角的两边,则两个角一定相等;③正三角形既是中心对称又是轴对称图形;④顺次连接对角线相等的四边形四边中点所得的四边形必是矩形;⑤三角形的内心到三角形的三个顶点的距离相等
A、0个 B、1个 C、2个 D、3个5. 如图,在中, , , 以点为圆心,以的长为半径作弧交于点 , 连接 , 再分别以点 , 为圆心,大于的长为半径作弧,两弧交于点 , 作射线交于点 , 连接 , 则下列结论中不正确的是( ) A、 B、垂直平分线段 C、 D、6. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子来量竿,却比竿子短一托.”其大意为,现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,根据题意,可列方程组为()A、 B、 C、 D、7. 在同一平面直角坐标系xOy中,一次函数y=ax与二次函数y=ax2+a的图象可能是( ).A、
A、 B、垂直平分线段 C、 D、6. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子来量竿,却比竿子短一托.”其大意为,现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,根据题意,可列方程组为()A、 B、 C、 D、7. 在同一平面直角坐标系xOy中,一次函数y=ax与二次函数y=ax2+a的图象可能是( ).A、 B、
B、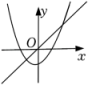 C、
C、 D、
D、 8. 如图,中, , 将绕点逆时针旋转得到 , 恰好经过点则阴影部分的面积为( )
8. 如图,中, , 将绕点逆时针旋转得到 , 恰好经过点则阴影部分的面积为( ) A、 B、 C、 D、9. 如图,在中,平分 , 于点 , , 若 , , 则的值为( )
A、 B、 C、 D、9. 如图,在中,平分 , 于点 , , 若 , , 则的值为( ) A、 B、 C、 D、10. 如图,正方形中,点是边上的动点不与点、重合 , 以为边向右作正方形 , 连接 , 点是的中点,连接、下列结论:
A、 B、 C、 D、10. 如图,正方形中,点是边上的动点不与点、重合 , 以为边向右作正方形 , 连接 , 点是的中点,连接、下列结论:
≌;
平分;
若 , , 则;
若 , 则 .
其中正确的有( )
A、个 B、个 C、个 D、个二、填空题(本大题共8小题,共24.0分)
-
11. 若在实数范围内有意义,则x的取值范围是 .12. 分解因式: .13. 《全国防沙治沙规划(年》》正式印发实施,提出到2030年,规划完成沙化土地治理任务1.86亿亩.数据“1.86亿”用科学记数法表示为 .14. 如图,直线 , , , 则等于度.
 15. 已知函数的图象与x轴有交点,则k的取值范围是 .16. 如图,在平面直角坐标系中,点为第一象限内一点,且.连结 , 并以点为旋转中心把逆时针转90°后得线段.若点恰好都在同一反比例函数的图象上,则的值等于.
15. 已知函数的图象与x轴有交点,则k的取值范围是 .16. 如图,在平面直角坐标系中,点为第一象限内一点,且.连结 , 并以点为旋转中心把逆时针转90°后得线段.若点恰好都在同一反比例函数的图象上,则的值等于. 17. 如图,是的直径, , 两点在圆上,连接 , , 且 , , 为上一动点,在运动过程中,与相交于点 , 当为等腰三角形时,的度数为 .
17. 如图,是的直径, , 两点在圆上,连接 , , 且 , , 为上一动点,在运动过程中,与相交于点 , 当为等腰三角形时,的度数为 . 18. 如图,在中, , , 点是边的中点,点是边上的一动点不与重合 , 连接 , 将沿翻折得 , 连接、 , 当线段的长取最小值时,的长为 .
18. 如图,在中, , , 点是边的中点,点是边上的一动点不与重合 , 连接 , 将沿翻折得 , 连接、 , 当线段的长取最小值时,的长为 .
三、解答题(本大题共8小题,共96.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 先化简,再求值: ,其中a满足 .20. “春节”是我国的传统佳节,民间历来有吃“饺子”的习俗我市某食品厂为了解市民对去年销量较好的猪肉馅饺、牛肉馅饺、虾肉馅饺、素馅饺以下分别用、、、表示这四种不同口味饺子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图尚不完整 .

请根据以上信息回答
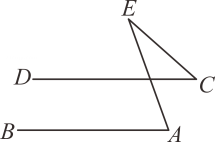
(1)、本次参加抽样调查的居民有人;(2)、将两幅不完整的图补充完整;(3)、若居民区有人,请估计爱吃饺的人数;(4)、若有外型完全相同的、、、饺子各一个,煮熟后,小王吃了两个用列表或画树状图的方法,求他吃到饺的概率.21. 多功能家庭早餐机可以制作多种口味的美食,深受消费者的喜爱,在新品上市促销活动中,已知8台A型早餐机和3台B型早餐机需要1000元,6台A型早餐机和1台B型早餐机需要600元.(1)、每台A型早餐机和每台B型早餐机的价格分别是多少元?(2)、某商家欲购进A,B两种型号早餐机共20台,但总费用不超过2200元,那么至少要购进A型早餐机多少台?22. 如图1所示是一种太阳能路灯,它由灯杆和灯管支架两部分构成如图2,是灯杆,是灯管支架,灯管支架与灯杆间的夹角.综合实践小组的同学想知道灯管支架的长度,他们在地面的点E处测得灯管支架底部D的仰角为60°,在点F处测得灯管支架顶部C的仰角为30°,测得m,m(A,E,F在同一条直线上).根据以上数据,解答下列问题: (1)、求灯管支架底部距地面高度的长(结果保留根号);(2)、求灯管支架的长度(结果精确到0.1m,参考数据:).23. 如图,是的直径,点在的延长线上, , , 交的延长线于点 .
(1)、求灯管支架底部距地面高度的长(结果保留根号);(2)、求灯管支架的长度(结果精确到0.1m,参考数据:).23. 如图,是的直径,点在的延长线上, , , 交的延长线于点 .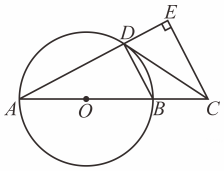 (1)、求证:与相切:(2)、若 , , 求的长.24. 为实施“乡村振兴”计划,某村产业合作社种植了“千亩桃园”.2022年该村桃子丰收,销售前对本地市场进行调查发现:当批发价为4千元/吨时,每天可售出12吨,每吨涨1千元,每天销量将减少2吨,据测算,每吨平均投入成本2千元,为了抢占市场,薄利多销,该村产业合作社决定,批发价每吨不低于4千元,不高于5.5千元.请解答以下问题:(1)、求每天销量y(吨)与批发价x(千元/吨)之间的函数关系式,并直接写出自变量x的取值范围;(2)、当批发价定为多少时,每天所获利润最大?最大利润是多少?25. 在中, , , 点 , 分别是 , 的中点,点是射线上一点,连接 , 将线段绕点顺时针旋转得到线段 , 连接 , .
(1)、求证:与相切:(2)、若 , , 求的长.24. 为实施“乡村振兴”计划,某村产业合作社种植了“千亩桃园”.2022年该村桃子丰收,销售前对本地市场进行调查发现:当批发价为4千元/吨时,每天可售出12吨,每吨涨1千元,每天销量将减少2吨,据测算,每吨平均投入成本2千元,为了抢占市场,薄利多销,该村产业合作社决定,批发价每吨不低于4千元,不高于5.5千元.请解答以下问题:(1)、求每天销量y(吨)与批发价x(千元/吨)之间的函数关系式,并直接写出自变量x的取值范围;(2)、当批发价定为多少时,每天所获利润最大?最大利润是多少?25. 在中, , , 点 , 分别是 , 的中点,点是射线上一点,连接 , 将线段绕点顺时针旋转得到线段 , 连接 , . (1)、如图 , 当点与点重合时,线段与的数量关系是 , ;(2)、如图当点在射线上运动时不与点 , 重合 , 求的值;(3)、连接 , 当是等边三角形时,请直接写出的值.26. 如图,直线与轴交于点 , 与轴交于 , 抛物线经过、两点,与轴正半轴交于点 , 为抛物线的顶点,连接 .
(1)、如图 , 当点与点重合时,线段与的数量关系是 , ;(2)、如图当点在射线上运动时不与点 , 重合 , 求的值;(3)、连接 , 当是等边三角形时,请直接写出的值.26. 如图,直线与轴交于点 , 与轴交于 , 抛物线经过、两点,与轴正半轴交于点 , 为抛物线的顶点,连接 .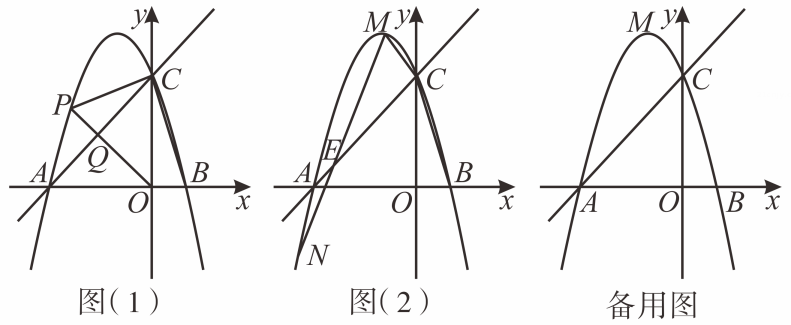 (1)、求抛物线的解析式及顶点的坐标;(2)、如图 , 点为直线上方的抛物线上的一点,连接、、 , 交于点 , 若将的面积分为:两部分,求点的坐标;(3)、如图 , 若点是第三象限的抛物线上一点,连接 , 交直线于 , 当时,求点的坐标;(4)、在(3)的条件下,若是轴上的一个动点,请直接写出的最小值.
(1)、求抛物线的解析式及顶点的坐标;(2)、如图 , 点为直线上方的抛物线上的一点,连接、、 , 交于点 , 若将的面积分为:两部分,求点的坐标;(3)、如图 , 若点是第三象限的抛物线上一点,连接 , 交直线于 , 当时,求点的坐标;(4)、在(3)的条件下,若是轴上的一个动点,请直接写出的最小值.