辽宁省鞍山市2023年中考数学试卷
试卷更新日期:2023-09-11 类型:中考真卷
一、选择题(本大题共8小题,每小题只有一个选项符合题意,每小题3分,共24分)
-
1. 的绝对值是( )A、 B、 C、 D、2. 如图所示的几何体是由5个完全相同的小正方体搭成的,它的左视图是( )
 A、
A、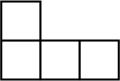
B、
B、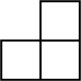 C、
C、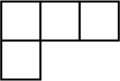
D、
D、
3. 下列运算正确的是( )A、 B、 C、 D、4. 九班名同学在一次测试中,某道题目满分分的得分情况如表:
3. 下列运算正确的是( )A、 B、 C、 D、4. 九班名同学在一次测试中,某道题目满分分的得分情况如表:得分分
人数
则这道题目得分的众数和中位数分别是( )
A、 , B、 , C、 , D、 ,5. 甲、乙两台机器运输某种货物,已知乙比甲每小时多运60kg,甲运输500kg所用的时间与乙运输800kg所用的时间相等,求甲、乙两台机器每小时分别运输多少千克货物,设甲每小时运输xkg货物,则可列方程为( )A、 B、 C、 D、6. 如图,直线 , 将含有角的直角三角尺按如图所示的位置放置,若 , 那么的大小为( )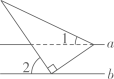 A、 B、 C、 D、7. 如图, , 为的两条弦,、分别为 , 的中点,的半径为若 , 则的长为( )
A、 B、 C、 D、7. 如图, , 为的两条弦,、分别为 , 的中点,的半径为若 , 则的长为( ) A、 B、 C、 D、8. 如图,在矩形ABCD中,对角线AC、BD交于点O,AB=4, , 垂直于BC的直线MN从AB出发,沿BC方向以每秒个单位长度的速度平移,当直线MN与CD重合时停止运动,运动过程中MN分别交矩形的对角线AC、BD于点E,F,以EF为边在MN左侧作正方形EFGH,设正方形EFGH与△AOB重叠部分的面积S,直线MN的运动时间为ts,则下列图象能大致反映s与t之间函数关系的是( )
A、 B、 C、 D、8. 如图,在矩形ABCD中,对角线AC、BD交于点O,AB=4, , 垂直于BC的直线MN从AB出发,沿BC方向以每秒个单位长度的速度平移,当直线MN与CD重合时停止运动,运动过程中MN分别交矩形的对角线AC、BD于点E,F,以EF为边在MN左侧作正方形EFGH,设正方形EFGH与△AOB重叠部分的面积S,直线MN的运动时间为ts,则下列图象能大致反映s与t之间函数关系的是( )
 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题(每小题3分,共24分)
-
9. 2023年5月3日,被誉为近五年最火的“五一”假期圆满收官,据文旅部发布的数据显示,年“五一”假期天,全国国内旅游出游合计约为人次将数据用科学记数法可表示为 .10. 因式分解: .11. 在一个不透明的口袋中装有红球和白球共个,这些球除颜色外都相同,将口袋中的球搅匀后,从中随机摸出个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸球次,发现有次摸到红球,则口袋中红球约有个12. 若关于的一元二次方程有两个不相等的实数根,则的取值范围是 .13. 如图,在平面直角坐标系中,矩形的边 , 分别在轴、轴正半轴上,点在边上,将矩形沿折叠,点恰好落在边上的点处,若 , , 则点的坐标是 .
 14. 如图,中,在 , 上分别截取 , , 使 , 分别以 , 为圆心,以大于的长为半径作弧,两弧在内交于点 , 作射线 , 交于点 , 过点作 , 垂足为点若 , , , 则的长为 .
14. 如图,中,在 , 上分别截取 , , 使 , 分别以 , 为圆心,以大于的长为半径作弧,两弧在内交于点 , 作射线 , 交于点 , 过点作 , 垂足为点若 , , , 则的长为 . 15. 如图,在中, , 顶点 , 分别在轴的正、负半轴上,点在第一象限,经过点的反比例函数的图象交于点 , 过点作轴,垂足为点 , 若点为的中点, , , 则的值为 .
15. 如图,在中, , 顶点 , 分别在轴的正、负半轴上,点在第一象限,经过点的反比例函数的图象交于点 , 过点作轴,垂足为点 , 若点为的中点, , , 则的值为 . 16. 如图,在正方形中,点为边上一点,连接 , 将绕点顺时针旋转得到 , 在 , 上分别截取 , , 使 , 连接 , 交对角线于点 , 连接并延长交于点若 , , 则的长为 .
16. 如图,在正方形中,点为边上一点,连接 , 将绕点顺时针旋转得到 , 在 , 上分别截取 , , 使 , 连接 , 交对角线于点 , 连接并延长交于点若 , , 则的长为 .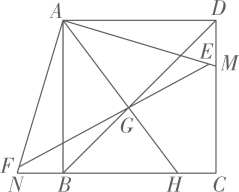
三、解答题(共102分)
-
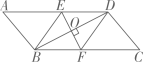
17. 先化简,再求值: , 其中 .18. 如图,在▱中,对角线的垂直平分线分别与 , , 相交于点 , , , 连接 , , 求证:四边形是菱形.
 19. 在第六十个学雷锋纪念日到来之际,习近平总书记指出:实践证明,无论时代如何变迁,雷锋精神永不过时,某校为弘扬雷锋精神,组织全校学生开展了手抄报评比活动评比结果共分为四项:非凡创意;魅力色彩; , 最美设计:无限潜力参赛的每名学生都恰好获得其中一个奖项,活动结束后,学校数学兴趣小组随机调查了部分学生的获奖情况,将调查结果绘制成如下两幅不完整的统计图.
19. 在第六十个学雷锋纪念日到来之际,习近平总书记指出:实践证明,无论时代如何变迁,雷锋精神永不过时,某校为弘扬雷锋精神,组织全校学生开展了手抄报评比活动评比结果共分为四项:非凡创意;魅力色彩; , 最美设计:无限潜力参赛的每名学生都恰好获得其中一个奖项,活动结束后,学校数学兴趣小组随机调查了部分学生的获奖情况,将调查结果绘制成如下两幅不完整的统计图.
请根据统计图提供的信息,解答下列问题:
(1)、本次共调查了名学生.(2)、请补全条形统计图.(3)、本次评比活动中,全校有名学生参加,根据调查结果,请你估计在评比中获得“非凡创意”奖的学生人数.20. 二十四节气是中国古代一种用来指导农事的补充历法,在国际气象界被誉为“中国的第五大发明”,并位列联合国教科文组织人类非物质文化遗产代表作名录,小明和小亮对二十四节气非常感兴趣,在课间玩游戏时,准备了四张完全相同的不透明卡片,卡片正面分别写有“惊蛰”“夏至”“白露”“霜降”四个节气,两人商量将卡片背面朝上洗匀后,从中随机抽取一张,并讲述所抽卡片上的节气的由来与习俗.(1)、小明从四张卡片中随机抽取一张卡片,抽到“惊蛰”的概率是 .(2)、小明先从四张卡片中随机抽取一张,小亮再从剩下的卡片中随机抽取一张,请用列表或画树状图的方法,求两人都没有抽到“夏至”的概率.21. 某商店窗前计划安装如图所示的遮阳棚,其截面图如图所示,在截面图中,墙面垂直于地面 , 遮阳棚与墙面连接处点距地面高 , 即 , 遮阳棚与窗户所在墙面垂直,即 , 假设此地正午时太阳光与地面的夹角恰为若经过点的光线恰好照射在地面点处,则 , 为使正午时窗前地面上能有宽的阴影区域,即 , 求遮阳棚的宽度结果精确到 , 参考数据: 22. 如图,直线与反比例函数的图象交于点 , , 过点作轴交轴于点 , 在轴正半轴上取一点 , 使 , 连接 , , 若的面积是 .
22. 如图,直线与反比例函数的图象交于点 , , 过点作轴交轴于点 , 在轴正半轴上取一点 , 使 , 连接 , , 若的面积是 . (1)、求反比例函数的解析式.(2)、点为第一象限内直线上一点,且的面积等于面积的倍,求点的坐标.23. 如图,四边形内接于 , 为的直径,过点作 , 交的延长线于点 , 交的延长线于点 , 连接若 .
(1)、求反比例函数的解析式.(2)、点为第一象限内直线上一点,且的面积等于面积的倍,求点的坐标.23. 如图,四边形内接于 , 为的直径,过点作 , 交的延长线于点 , 交的延长线于点 , 连接若 .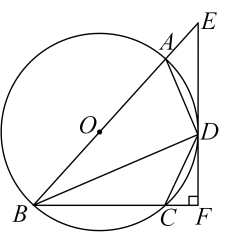 (1)、求证:为的切线.(2)、若 , , 求的半径.24. 网络销售已经成为一种热门的销售方式,某果园在网络平台上直播销售荔枝已知该荔枝的成本为元 , 销售价格不高于元 , 且每售卖需向网络平台支付元的相关费用,经过一段时间的直播销售发现,每日销售量与销售价格元之间满足如图所示的一次函数关系.
(1)、求证:为的切线.(2)、若 , , 求的半径.24. 网络销售已经成为一种热门的销售方式,某果园在网络平台上直播销售荔枝已知该荔枝的成本为元 , 销售价格不高于元 , 且每售卖需向网络平台支付元的相关费用,经过一段时间的直播销售发现,每日销售量与销售价格元之间满足如图所示的一次函数关系. (1)、求与的函数解析式.(2)、当每千克荔枝的销售价格定为多少元时,销售这种荔枝日获利最大,最大利润为多少元?25. 如图,在中, , , 点是射线上的动点不与点 , 重合 , 连接 , 过点在左侧作 , 使 , 连接 , 点 , 分别是 , 的中点,连接 , , .
(1)、求与的函数解析式.(2)、当每千克荔枝的销售价格定为多少元时,销售这种荔枝日获利最大,最大利润为多少元?25. 如图,在中, , , 点是射线上的动点不与点 , 重合 , 连接 , 过点在左侧作 , 使 , 连接 , 点 , 分别是 , 的中点,连接 , , . (1)、如图 , 点在线段上,且点不是的中点,当 , 时,与的位置关系是 , .(2)、如图 , 点在线段上,当 , 时,求证: .(3)、当 , 时,直线与直线交于点 , 若 , , 请直接写出线段的长.26. 如图 , 抛物线经过点 , 与轴交于点 , 点为第一象限内抛物线上一动点.
(1)、如图 , 点在线段上,且点不是的中点,当 , 时,与的位置关系是 , .(2)、如图 , 点在线段上,当 , 时,求证: .(3)、当 , 时,直线与直线交于点 , 若 , , 请直接写出线段的长.26. 如图 , 抛物线经过点 , 与轴交于点 , 点为第一象限内抛物线上一动点.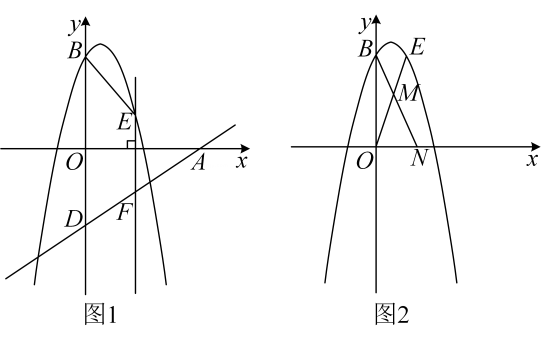 (1)、求抛物线的解析式.(2)、直线与轴交于点 , 与轴交于点 , 过点作直线轴,交于点 , 连接 , 当时,求点的横坐标.(3)、如图 , 点为轴正半轴上一点,与交于点 , 若 , , 求点的坐标.
(1)、求抛物线的解析式.(2)、直线与轴交于点 , 与轴交于点 , 过点作直线轴,交于点 , 连接 , 当时,求点的横坐标.(3)、如图 , 点为轴正半轴上一点,与交于点 , 若 , , 求点的坐标.