浙江省A9协作体2023-2024学年高二上学期暑假返校联考数学试题
试卷更新日期:2023-09-11 类型:开学考试
一、单选题
-
1. 若 , 则复数的虚部为( )A、i B、1 C、-1 D、-i2. 如图所示,等腰梯形是平面图形ABCD用斜二测画法得到的直观图, , 则平面图形ABCD的面积为( )
 A、 B、12 C、 D、63. 抛掷两枚质地均匀的骰子,记事件A=“第一枚骰子奇数面朝上”,事件B=“第二枚骰子偶数面朝上”,事件C=“两枚骰子向上点数之和为7”.则下列结论正确的是( )A、A与B对立 B、A与C互斥 C、 D、B与C独立4. 已知向量 , , 若是在上的投影向量,则( )A、 B、 C、 D、5. 在中,内角A,B,C所对的边分别为 , , , 将该三角形绕AC边旋转360°得一个旋转体,则该旋转体体积为( )A、 B、 C、 D、6. 一组数据由6个数组成,将其中一个数由4改为6,另一个数由12改为10,其余数不变,得到新的一组数据,则新的一组数的方差减去原一组数的方差的差为( )A、4 B、3 C、-4 D、-37. 如图,点、、、、为正方体的顶点或所在棱的中点,则下列各图中,不满足直线平面的是( )A、
A、 B、12 C、 D、63. 抛掷两枚质地均匀的骰子,记事件A=“第一枚骰子奇数面朝上”,事件B=“第二枚骰子偶数面朝上”,事件C=“两枚骰子向上点数之和为7”.则下列结论正确的是( )A、A与B对立 B、A与C互斥 C、 D、B与C独立4. 已知向量 , , 若是在上的投影向量,则( )A、 B、 C、 D、5. 在中,内角A,B,C所对的边分别为 , , , 将该三角形绕AC边旋转360°得一个旋转体,则该旋转体体积为( )A、 B、 C、 D、6. 一组数据由6个数组成,将其中一个数由4改为6,另一个数由12改为10,其余数不变,得到新的一组数据,则新的一组数的方差减去原一组数的方差的差为( )A、4 B、3 C、-4 D、-37. 如图,点、、、、为正方体的顶点或所在棱的中点,则下列各图中,不满足直线平面的是( )A、 B、
B、 C、
C、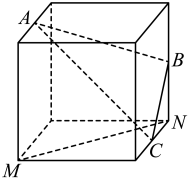 D、
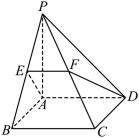
D、 8. 五面体ABCDEF中,底面ABCD为矩形,AB=3, , △ADE与都是边长为2的等边三角形,若点A,B,C,D,E,F都在球O的球面上,则球O的表面积为( )A、 B、 C、 D、
8. 五面体ABCDEF中,底面ABCD为矩形,AB=3, , △ADE与都是边长为2的等边三角形,若点A,B,C,D,E,F都在球O的球面上,则球O的表面积为( )A、 B、 C、 D、二、多选题
-
9. 有一组样本数据 , 另一组样本数据 , 其中 , c为非零常数,则( )A、两组样本数据平均数相同 B、两组样本数据方差相同 C、两组样本数据中位数相等 D、两组样本数据极差相同10. 在复平面内,复数 , 则( )A、的模长为1 B、在复平面内对应的点在第二象限 C、 D、复数满足 , 则11. 已知l,m,n是三条不同的直线,α,β,γ是三个不同的平面,则( )A、已知 , , , 若 , 则 B、若 , , , 则 C、若 , , , 则 D、若 , , 则12. 在中,内角A、B、C所对的边分别为 , 则( )A、若A>B,则 B、若 , a=1,则最大值为 C、若 , b=4, , 则满足条件的三角形有两个 D、若 , 且 , 则为等边三角形
三、填空题
-
13. 复数是关于的方程的一个根,则 .14. 某人在湖面之上2米处测得空中一气球的仰角为30°,且测得湖中气球倒影的俯角为60°,若不考虑水的折射和球的体积,则气球离水面的高度为米.15. 在△ABC中,内角A、B、C所对应的边分别为a、b、c,a= , b=2,C=2B,则AB的长为.16. 已知三棱锥ABCD中,AB⊥CD,且CD与平面ABD所成角余弦值为 , 当取得最大值时,二面角C-AB-D的正弦值为 .
四、解答题
-
17. 已知向量与的夹角为 , 且 , 是单位向量.(1)、分别求和的值;(2)、若与共线,求 .18. 杭州2022年第19届亚运会将于2023年9月23日至10月8日举行.随着亚运会的临近,亚运会的热度持续提升.为让更多的人了解亚运会运动项目和亚运精神,某中学举办了亚运会知识竞赛,并从中随机抽取了100名学生的成绩,绘制成如图所示的频率分布直方图.
 (1)、试根据频率分布直方图求出这100名学生中成绩低于60分的人数;(2)、试估计这100名学生成绩的第75百分位数;(3)、若采用分层抽样的方法从成绩在 , , 的学生中共抽取6人参加志愿者活动.现从这6人中随机抽取2人分享活动经验,求抽取的2人成绩都在的概率.19. 在中,内角A,B,C所对的边分别为a,b,c,且 .(1)、求角A;(2)、若a= , c=2,的角平分线交BC于D,求AD的长.
(1)、试根据频率分布直方图求出这100名学生中成绩低于60分的人数;(2)、试估计这100名学生成绩的第75百分位数;(3)、若采用分层抽样的方法从成绩在 , , 的学生中共抽取6人参加志愿者活动.现从这6人中随机抽取2人分享活动经验,求抽取的2人成绩都在的概率.19. 在中,内角A,B,C所对的边分别为a,b,c,且 .(1)、求角A;(2)、若a= , c=2,的角平分线交BC于D,求AD的长.