浙江省嘉兴市海盐县2023-2024学年高二上学期返校评估测试数学试卷

试卷更新日期：2023-09-11 类型：开学考试

进入出卷网下载

一、单选题（40分）

1. 已知 $z = \frac{3 + i}{2 i}$ ，则 $z =$ （）

A、 $\frac{1}{2} + \frac{3}{2} i$ B、 $\frac{1}{2} - \frac{3}{2} i$ C、 $\frac{3}{2} + \frac{1}{2} i$ D、 $\frac{3}{2} - \frac{1}{2} i$

查看试题解析
2. 已知平面向量 $\vec{a} = (- 1 ， 2)$ ， $\vec{b} = (3 ， - 1)$ ， $\vec{c} = (t ， t)$ ，若 $(\vec{a} + \vec{c})$ ∥ $\vec{b}$ ，则 $\vec{a} \cdot \vec{c} =$ （）

A、 $\frac{5}{2}$ B、 $\frac{1}{4}$ C、 $- \frac{5}{4}$ D、 $- \frac{7}{4}$

查看试题解析

3. 甲、乙、丙、丁四人参加奥运会射击项目选拔赛，四人的平均成绩和方差如表所示：从这四个人中选择一人参加奥运会射击项目比赛，最佳人选是（）

	甲	乙	丙	丁
平均成绩 $\bar{x}$	8.6	8.9	8.9	8.2
方差 $s^{2}$	3.5	5.6	2.1	3.5

A、甲 B、乙 C、丙 D、丁

查看试题解析

4. 从长度为 $2 ， 4 ， 6 ， 8 ， 10$ 的5条线段中任取3条，则这3条线段能构成一个三角形的概率是（）

A、 $\frac{3}{10}$ B、 $\frac{3}{5}$ C、 $\frac{3}{8}$ D、 $\frac{1}{3}$

查看试题解析
5. 如图，若直线 $l_{1} ， l_{2} ， l_{3}$ 的斜率分别为 $k_{1} ， k_{2} ， k_{3}$ ，则（）

A、 $k_{1} < k_{3} < k_{2}$ B、 $k_{3} < k_{1} < k_{2}$ C、 $k_{1} < k_{2} < k_{3}$ D、 $k_{3} < k_{2} < k_{1}$

查看试题解析
6. 已知直线 $l_{1}$ 过点 $A (2 ， - 3) ， B (4 ， 0)$ ，且 $l_{1} ⊥ l_{2}$ ，则直线 $l_{2}$ 的斜率为（）

A、 $\frac{2}{3}$ B、 $- \frac{2}{3}$ C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
7. 已知 $s i n (\frac{π}{6} + α) = \frac{\sqrt{3}}{3}$ ，且 $α \in (- \frac{π}{4} ， \frac{π}{4})$ ，则 $s i n (\frac{π}{3} - α) =$ （）

A、 $- \frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{2}}{3}$ D、 $\frac{\sqrt{6}}{3}$

查看试题解析
8. 在四棱锥P－ABCD中，PA⊥平面ABCD，ABCD是矩形，且AB＝3，AD＝4，PA＝ $\frac{4 \sqrt{3}}{5}$ ，则锐二面角 $A - B D - P$ 的大小为（）

A、30° B、45° C、60° D、75°

查看试题解析

二、多选题（20分）

9. 若甲组样本数据 $x_{1} ， x_{2} ， ⋯ ， x_{n}$ （数据各不相同）的平均数为3，乙组样本数据 $2 x_{1} + a ， 2 x_{2} + a ， ⋯ ， 2 x_{n} + a$ 的平均数为5，下列说错误的是（）

A、 $a$ 的值不确定 B、乙组样本数据的方差为甲组样本数据方差的2倍 C、两组样本数据的极差可能相等 D、两组样本数据的中位数可能相等

查看试题解析
10. 下列说法正确的是（）

A、从五名同学中选三名同学去听专家讲座，不同的选法有10种 B、甲袋中有8个白球，4个红球，乙袋中有6个白球，6个红球，从每袋中各任取一个球，则取到同色球的概率为 $\frac{1}{2}$ C、从装有2个红球，3个白球的不透明袋子中任取3个球，则事件“所取的3个球中至少有1个红球”与事件“3个都是白球”互为对立事件 D、设两个独立事件 $A$ 和 $B$ 都不发生的概率为 $\frac{1}{9}$ ， $A$ 发生 $B$ 不发生的概率与 $B$ 发生 $A$ 不发生的概率相同，则事件 $A$ 发生的概率是 $\frac{2}{9}$

查看试题解析
11. 已知函数 $f (x) = c o s^{2} x + s i n^{2} (x - \frac{π}{2})$ ，将函数 $f (x)$ 的图象先向右平移 $\frac{π}{12}$ 个单位长度，再向下平移1个单位长度得到函数 $g (x)$ 的图象，则下列说法正确的是（）

A、函数 $f (x)$ 为偶函数 B、 $g (x) = c o s (2 x + \frac{π}{6})$ C、 $g (x) = c o s (2 x - \frac{π}{6})$ D、函数 $g (x)$ 的图象的对称轴方程为 $x = \frac{k π}{2} + \frac{π}{12} (k \in Z)$

查看试题解析
12. 在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $M$ 为棱 $A A_{1}$ 上的动点（含端点），则下列说法正确的是（）

A、存在点 $M$ ，使得 $C_{1} M / /$ 平面 $A B_{1} C$ B、对于任意点 $M$ ，都有平面 $C_{1} M B ⊥$ 平面 $A_{1} B_{1} C D$ C、异面直线 $C_{1} M$ 与 $B C$ 所成角的余弦值的取值范围是 $[\frac{1}{2} ， \frac{\sqrt{2}}{2}]$ D、若 $C_{1} M ⊥$ 平面 $α$ ，则平面 $α$ 截该正方体的截面图形的周长最大值为 $6 \sqrt{2}$

查看试题解析

三、填空题（20分）

13. 已知向量 $\vec{a}$ ， $\vec{b}$ 的夹角为60°，| $\vec{a}$ |=2，| $\vec{b}$ |=1，则| $\vec{a}$ +2 $\vec{b}$ |= ．

查看试题解析
14. 若经过点 $P (1 - a ， 1)$ 和 $Q (2 a ， 3)$ 的直线的倾斜角是钝角，则实数 $a$ 的取值范围是．

查看试题解析
15. 在△ABC中，内角A，B，C的对边分别为a，b，c，若△ABC的面积为S，且a＝1， $4 S = b^{2} + c^{2} - a^{2}$ ，则△ABC外接圆的半径为．

查看试题解析
16. 直四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的底面正方形边长为 $2$ ，侧棱长为 $\sqrt{3}$ ，以顶点 $A$ 为球心， $2$ 为半径作一个球，则球面与直四棱柱的表面相交所得到的所有弧长之和等于．

查看试题解析

四、解答题（10+12+12+12+12+12）

17. 已知平面向量 $\vec{a} = (1 ， 3) ， \vec{b} = (6 ， 2 x)$ .

(1)、若 $2 \vec{a} + \vec{b}$ 与 $2 \vec{a} - \vec{b}$ 垂直，求 $x$ 的值；

(2)、若向量 $\vec{c} = (5 ， - 1)$ ，若 $\vec{a} + \vec{b}$ 与 $\vec{b} - \vec{c}$ 共线，求 $| \vec{a} - \vec{b} |$ .

查看试题解析
18. 从某学校的800名男生中随机抽取50名测量身高，被测学生身高全部介于155cm和195cm之间，将测量结果按如下方式分成八组：第一组 $[155 ， 160)$ ，第二组 $[160 ， 165)$ ， $⋯$ ，第八组 $[190 ， 195]$ ，下图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第六组的人数为4人．

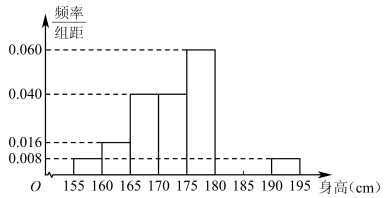(1)、求第七组的频率；

(2)、估计该校的800名男生的中位数；

(3)、若从身高属于第六组和第八组的所有男生中随机抽取两名男生，记他们的身高分别为x，y，事件 $E = {| x - y | \leq 5}$ ，求 $P (E)$ ．

查看试题解析
19. 在 $△ A B C$ 中，内角 $A$ ， $B$ ， $C$ 的对边分别是 $a$ ， $b$ ， $c$ ，且满足 $(a + c) (s i n A - s i n C) = (\sqrt{3} a - b) s i n$ B.

(1)、求角 $C$ 的值.

(2)、 $s i n A s i n B = \frac{\sqrt{3}}{4}$ ， $c = 2$ ，求 $△ A B C$ 的面积．

查看试题解析
20. 四棱锥 $P － A B C D$ 中 $， P A$ ⊥平面 $A B C D ，$ 四边形 $A B C D$ 为菱形 $， ∠ A D C = 60 ° ， P A = A D = 2 ， E$ 为 $A D$ 的中点．

(1)、求证：平面 $P C E ⊥$ 平面 $P A D$ ；

(2)、求 $P C$ 与平面 $P A D$ 所成的角的正切值；

(3)、求二面角 $A － P D － C$ 的正弦值．

查看试题解析
21. 在 $△ A B C$ 中，内角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ，且 $b c o s A - a c o s B = 2 c$ ．

(1)、证明： $t a n B = - 3 t a n A$ ；

(2)、若 $b^{2} + c^{2} = a^{2} + \sqrt{3} b c$ ，且 $△ A B C$ 的面积为 $\sqrt{3}$ ，求 $a$ ．

查看试题解析
22. 如图，在多面体 $A B C D E$ 中， $A E ⊥$ 平面 $A B C$ ，平面 $B C D ⊥$ 平面 $A B C$ ， $△ A B C$ 是边长为 $2$ 的等边三角形， $B D = C D = \sqrt{5}$ ， $A E = 2$ ．

(1)、求点B到平面ECD的距离；

(2)、求平面 $B E D$ 与平面 $A B C$ 所成锐二面角的余弦值．

查看试题解析