吉林省梅河口市重点中学2023-2024学年高三上册数学开学考试试卷
试卷更新日期:2023-09-11 类型:开学考试
一、选择题:本题共8小题,每小题5分,共40分.在每小题所给的四个选项中,只有一项是符合题目要求的.
-
1. 设全集U=R,A={x|0<x≤3},B={x|x<1},则图中阴影部分表示的集合为( )
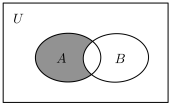 A、{x|1≤x<3} B、{x|1<x≤3} C、{x|1<x<3} D、{x|1≤x≤3}2. 已知(为虚数单位)是纯虚数,则( )A、 B、0 C、1 D、23. 已知双曲线的一条渐近线方程为 , 则的焦距为( )A、 B、 C、 D、4. 《几何原本》是古希腊数学家欧几里得的一部不朽之作,其第十一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥.如图,若都是直角圆锥底面圆的直径,且 , 则异面直线与所成角的余弦值为( )
A、{x|1≤x<3} B、{x|1<x≤3} C、{x|1<x<3} D、{x|1≤x≤3}2. 已知(为虚数单位)是纯虚数,则( )A、 B、0 C、1 D、23. 已知双曲线的一条渐近线方程为 , 则的焦距为( )A、 B、 C、 D、4. 《几何原本》是古希腊数学家欧几里得的一部不朽之作,其第十一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥.如图,若都是直角圆锥底面圆的直径,且 , 则异面直线与所成角的余弦值为( )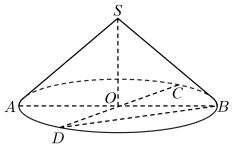 A、 B、 C、 D、5. 已知函数的部分图象如图所示,则函数的解析式可能为( )
A、 B、 C、 D、5. 已知函数的部分图象如图所示,则函数的解析式可能为( )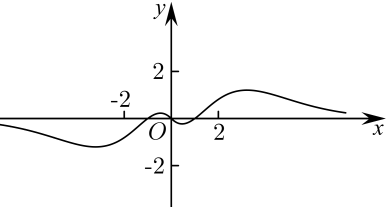 A、 B、 C、 D、6. 已知集合A={x∈N|x2<8x},B={2,3,6},C={2,3,7},则=( )A、{2,3,4,5} B、{2,3,4,5,6} C、{1,2,3,4,5,6} D、{1,3,4,5,6,7}7. 已知复数z , 则复数z的虚部为( )A、 B、 C、i D、i8. 已知集合A={y|y= },B={x|y=lg(x﹣2x2)},则∁R(A∩B)=( )A、[0, ) B、(﹣∞,0)∪[ ,+∞) C、(0, ) D、(﹣∞,0]∪[ ,+∞)
A、 B、 C、 D、6. 已知集合A={x∈N|x2<8x},B={2,3,6},C={2,3,7},则=( )A、{2,3,4,5} B、{2,3,4,5,6} C、{1,2,3,4,5,6} D、{1,3,4,5,6,7}7. 已知复数z , 则复数z的虚部为( )A、 B、 C、i D、i8. 已知集合A={y|y= },B={x|y=lg(x﹣2x2)},则∁R(A∩B)=( )A、[0, ) B、(﹣∞,0)∪[ ,+∞) C、(0, ) D、(﹣∞,0]∪[ ,+∞)二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对得5分,部分选对得2分,有选错的得0分)
-
9. 近年来、新冠疫情波及到千家万户,人们的生活方式和习惯不得不发生转变,短视频成了观众空闲时娱乐活动的首选.某电影艺术中心为了解短视频平台的观众年龄分布情况,向各大短视频平台的观众发放了线上调查问卷,共回收有效样本4000份,根据所得信息制作了如图所示的频率分布直方图,则下列说法正确的是( )
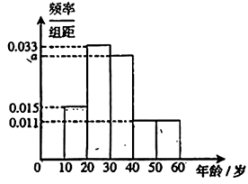 A、图中 B、在4000份有效样本中,短视频观众年龄在10~20岁的有1320人 C、估计短视频观众的平均年龄为32岁 D、估计短视频观众年龄的75%分位数为39岁10. 已知函数的图像关于直线对称,则( )A、满足 B、将函数的图像向左平移个单位长度后与图像重合 C、若 , 则的最小值为 D、若在上单调递减,那么的最大值是11. 已知直线 , 过直线上任意一点作圆的两条切线,切点分别为 , 则有( )A、长度的最小值为 B、不存在点使得为 C、当最小时,直线的方程为 D、若圆与轴交点为 , 则的最小值为2812. 已知直三棱柱中,是的中点,为的中点.点是上的动点,则下列说法正确的是( )
A、图中 B、在4000份有效样本中,短视频观众年龄在10~20岁的有1320人 C、估计短视频观众的平均年龄为32岁 D、估计短视频观众年龄的75%分位数为39岁10. 已知函数的图像关于直线对称,则( )A、满足 B、将函数的图像向左平移个单位长度后与图像重合 C、若 , 则的最小值为 D、若在上单调递减,那么的最大值是11. 已知直线 , 过直线上任意一点作圆的两条切线,切点分别为 , 则有( )A、长度的最小值为 B、不存在点使得为 C、当最小时,直线的方程为 D、若圆与轴交点为 , 则的最小值为2812. 已知直三棱柱中,是的中点,为的中点.点是上的动点,则下列说法正确的是( )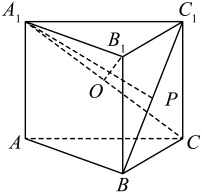 A、无论点在上怎么运动,都有 B、当直线与平面所成的角最大时,三棱锥的外接球表面积为 C、若三棱柱 , 内放有一球,则球的最大体积为 D、周长的最小值
A、无论点在上怎么运动,都有 B、当直线与平面所成的角最大时,三棱锥的外接球表面积为 C、若三棱柱 , 内放有一球,则球的最大体积为 D、周长的最小值三、填空题:本题共4小题,每小题5分,共20分.
-
13. 《易经》是中国传统文化中的精髓,如图是易经八卦(含乾、坤、巽、震、坎、离、艮、兑八卦),每一卦由三根线组成(""表示一根阳线,""表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为.
 14. 设直线过双曲线的一个焦点,且与的一条对称轴垂直,与交于两点,为的实轴长的2倍,则双曲线的离心率为.15. 已知椭圆的离心率是 , 若以为圆心且与椭圆C有公共点的圆的最大半径为 , 此时椭圆C的方程是16. 已知函数 ,若对于任意正实数 ,均存在以 为三边边长的三角形,则实数k的取值范围是.
14. 设直线过双曲线的一个焦点,且与的一条对称轴垂直,与交于两点,为的实轴长的2倍,则双曲线的离心率为.15. 已知椭圆的离心率是 , 若以为圆心且与椭圆C有公共点的圆的最大半径为 , 此时椭圆C的方程是16. 已知函数 ,若对于任意正实数 ,均存在以 为三边边长的三角形,则实数k的取值范围是.四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
-
17. 设等差数列的前n项和为 , 已知 , 各项均为正数的等比数列满足 .(1)、求数列与的通项公式;(2)、设 , 求数列的前项和 .18. 已知数列中, , 是公差为的等差数列.(1)、求的通项公式;(2)、若 , 为数列的前项和,证明:.19. 已知函数 .(1)、讨论 的单调性;(2)、若 在定义域内是增函数,且存在不相等的正实数 ,使得 ,证明: .20. 在 中,内角 的边长分别为 ,且 .(1)、若 , ,求 的值;(2)、若 ,且 的面积 ,求 和 的值.
